认知无线电中的能量检测算法研究(包含：不同SNR、不同噪声不确定性、不确定噪声和动态阈值比较)（Matlab代码实现）

最新推荐文章于 2025-05-01 22:32:29 发布

天天程序猿

最新推荐文章于 2025-05-01 22:32:29 发布

阅读量532

点赞数 18

文章标签：算法 matlab 数据结构

本文链接：https://blog.csdn.net/2301_77414277/article/details/145719115

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

认知无线电中能量检测算法研究：SNR、噪声不确定性与动态阈值的综合分析

一、能量检测算法的基本原理

二、不同SNR条件下的性能分析

四、不确定噪声场景下的改进方法

五、动态阈值设定策略比较

六、未来研究方向

结论

📚2 运行结果

2.1 不同的N值

2.2 不同的SNR

2.3 不同的噪声不确定性

2.4 不确定噪声和动态阈值比较

2.5 所有案例比较

🎉3 参考文献

🌈4 Matlab代码实现

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

认知无线电中能量检测算法研究：SNR、噪声不确定性与动态阈值的综合分析

一、能量检测算法的基本原理

能量检测（Energy Detection, ED）是认知无线电中最基础的频谱感知技术，其核心原理是将接收信号能量与预设阈值进行比较，判断信道是否被主用户（PU）占用。该过程可建模为二元假设问题：

二、不同SNR条件下的性能分析

高SNR场景
随着SNR增加，检测概率 PdPd 显著提升。例如，当SNR从-15 dB提升至-5 dB时，PdPd 可从接近0升至90%以上[21][56]。此时，信号能量远高于噪声，能量检测鲁棒性较强。
低SNR场景
当SNR低于-17 dB时，传统能量检测的 PdPd 趋近于0，此时需通过以下方法改善性能：
- 增加采样点数：延长观测时间可提升低SNR下的检测概率（例如，采样点数从100增至1000时，PdPd 提升约30%）[56]。
- 协作感知：多节点协作通过“或”准则融合结果，可突破单节点检测极限。例如，在SNR=-20 dB时，10节点协作可使 PdPd 从0提升至60%[56][83]。
- 机器学习辅助：基于k-NN或随机森林的算法在低SNR下表现优于传统ED，但高SNR时复杂度增加可能限制其应用[27].
动态SNR适应性
车联网等快速时变场景中，需结合多特征参数（如能量、协方差矩阵特征值）与神经网络分类，以保持跨SNR范围的稳定性。

四、不确定噪声场景下的改进方法

双阈值策略
- 固定双阈值：设置上下限 λLλL 和 λHλH，能量介于两者时触发重检或协作判决。例如，自适应双阈值在SNR=-10 dB时提升 PdPd 27-39%。
- 动态调整：基于历史能量或SNR权重系数调整阈值，避免固定阈值在NU下的失效。
噪声功率建模
- 均匀分布假设：NP-AVE/NP-AVN检测器通过平均似然比消除对噪声功率的依赖，在NU=3 dB时 PdPd 提升40%。
- Huber混合模型：鲁棒估计噪声方差，降低NU对阈值的影响。
协作感知优化
- 硬融合准则：OR准则在低SNR和小规模网络中表现最佳，Majority准则适用于大规模网络。
- 增强能量检测：结合协方差矩阵特征值分析，在非同分布噪声下最小化总错误率

五、动态阈值设定策略比较

方法	原理	优势	局限性
固定双阈值	预设上下限，能量介于区间时触发协作判决	复杂度低，适合实时系统	需先验NU范围，低SNR时无效
BPSO优化阈值	二进制粒子群算法动态优化阈值，最小化总感知错误	自适应性强，PdPd 提升显著（SNR=3 dB时优化后错误率降50%）	计算复杂度高，需离线训练
隐马尔可夫模型预测	结合信道状态预测与动态阈值调整	提升吞吐量，适用于时变信道	模型训练复杂，需大量历史数据
噪声功率实时测量	动态根据当前噪声水平调整阈值（如基于FFT的频域能量检测）	无需先验知识，鲁棒性高	实时计算资源需求较大

六、未来研究方向

多维度融合检测：结合能量、循环平稳特征与深度学习，突破SNR墙限制。
低复杂度动态阈值算法：探索轻量级优化算法（如遗传算法）在实时系统中的应用。
跨层设计：联合频谱感知与资源分配，优化系统级吞吐量与能耗。

结论

能量检测算法的性能受SNR、噪声不确定性及阈值策略的显著影响。在高SNR场景中，传统ED表现优异；低SNR时需结合协作感知与动态阈值优化。噪声不确定性可通过双阈值、均匀分布建模或机器学习方法缓解。未来研究需进一步平衡算法复杂度与性能，推动认知无线电在5G/6G及物联网中的实际应用。

📚2 运行结果

2.1 不同的N值

2.2 不同的SNR

2.3 不同的噪声不确定性

2.4 不确定噪声和动态阈值比较

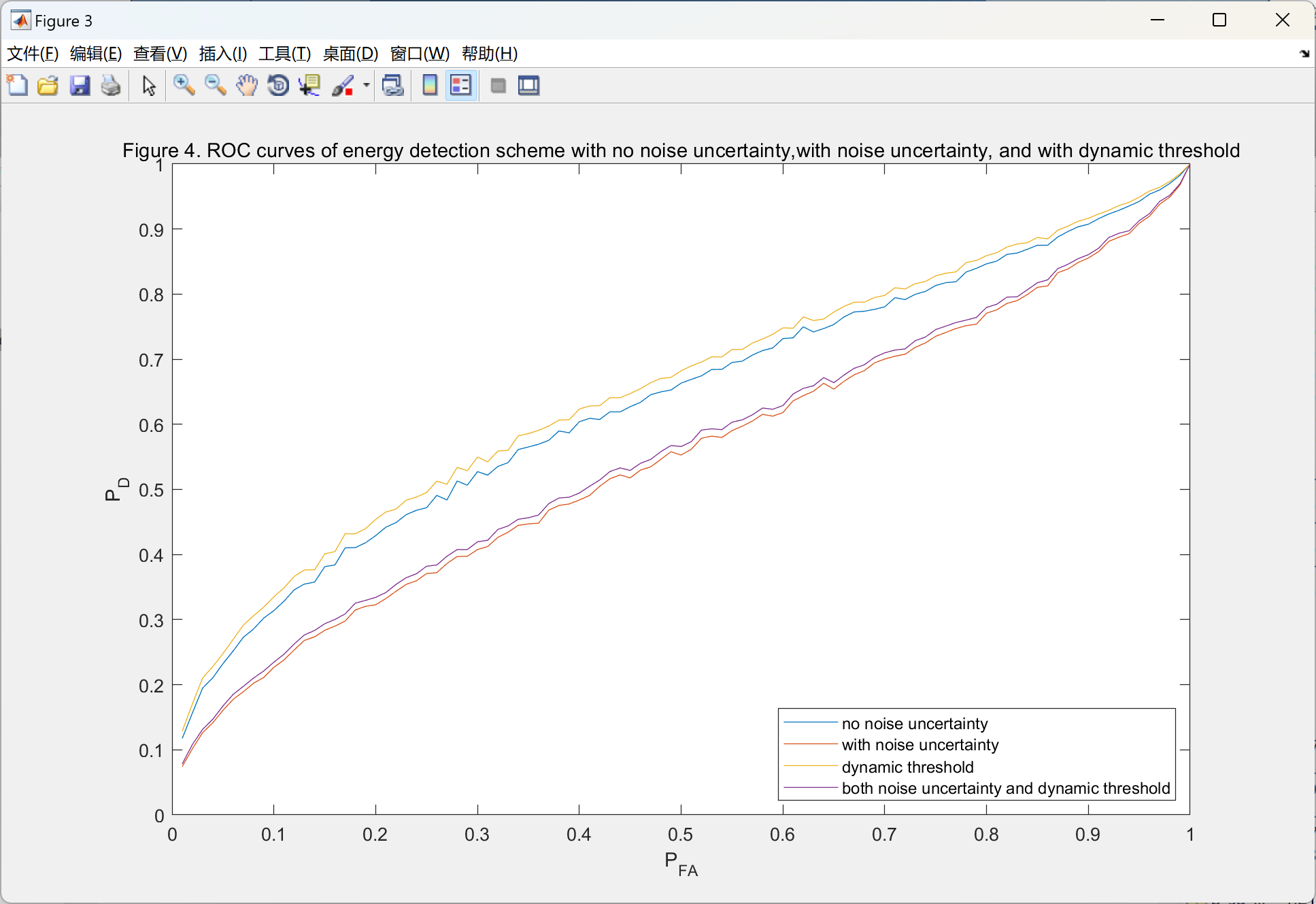
2.5 所有案例比较

部分代码：

%% Simulation to plot Probability of Detection (Pd) vs. Probability of False Alarm (Pf) 
for m = 1:length(Pf)
    
    i = 0;i2=0;i3=0;i4=0;
for kk=1:10000 % Number of Monte Carlo Simulations
 n = randn(1,L); n2 = sqrt(1.01).*randn(1,L);%AWGN noise with mean 0 and variance 
 %s = sqrt(snr).*randn(1,L); % Real valued Gaussina Primary User Signal 
 s = sqrt(snr).*bpsk_w;
 %s = 1/sqrt(2)*sqrt(snr).*randn(1,L)+randn(1,L);
 y = s + n;y2 = s + n2; % Received signal at SU
 energy = abs(y).^2;  energy2 = abs(y2).^2;% Energy of received signal over N samples
 energy_fin =(1/L).*sum(energy);energy_fin2 =(1/L).*sum(energy2); % Test Statistic for the energy detection
 thresh(m) = (qfuncinv(Pf(m))./sqrt(L))+ 1;  thresh2(m) = (qfuncinv(Pf(m)).*1.02./sqrt(L))+ 1.02;thresh3(m) = ((qfuncinv(Pf(m))./sqrt(L))+ 1)./1.002;thresh4(m) = ((qfuncinv(Pf(m)).*1.02./sqrt(L))+ 1.02)./1.001;% Theoretical value of Threshold, refer, Sensing Throughput Tradeoff in Cognitive Radio, Y. C. Liang
 if(energy_fin >= thresh(m))  % Check whether the received energy is greater than threshold, if so, increment Pd (Probability of detection) counter by 1
     i = i+1;
 end
  if(energy_fin2 >= thresh2(m))  % Check whether the received energy is greater than threshold, if so, increment Pd (Probability of detection) counter by 1
     i2 = i2+1;