简单背包问题

2301_78981471

已于 2023-12-19 13:29:55 修改

阅读量970

点赞数 24

分类专栏：算法学习记录文章标签：笔记算法 c++

于 2023-12-18 21:57:27 首次发布

本文链接：https://blog.csdn.net/2301_78981471/article/details/135065651

版权

算法学习记录专栏收录该内容

32 篇文章 0 订阅

订阅专栏

01背包

简介

01背包就是指问题：从 $N$ 件物品中选出 $k$ 件放入容量是 $V$ 的背包中，最终答案具有某种属性（价值最大/最小/物品数量最多…），而且每种物品只能选一次。

思路

任何 $D p$ 问题，都经过这么一轮分析：状态表示 + 状态计算。

状态表示：是从集合的角度来理解问题，分为集合与属性。
- 哪个集合[i, j]
- 集合的属性（最大最小值等）：就是存储的值f[i, j]
状态计算：分析集合怎么计算，也就是找状态转移方程。

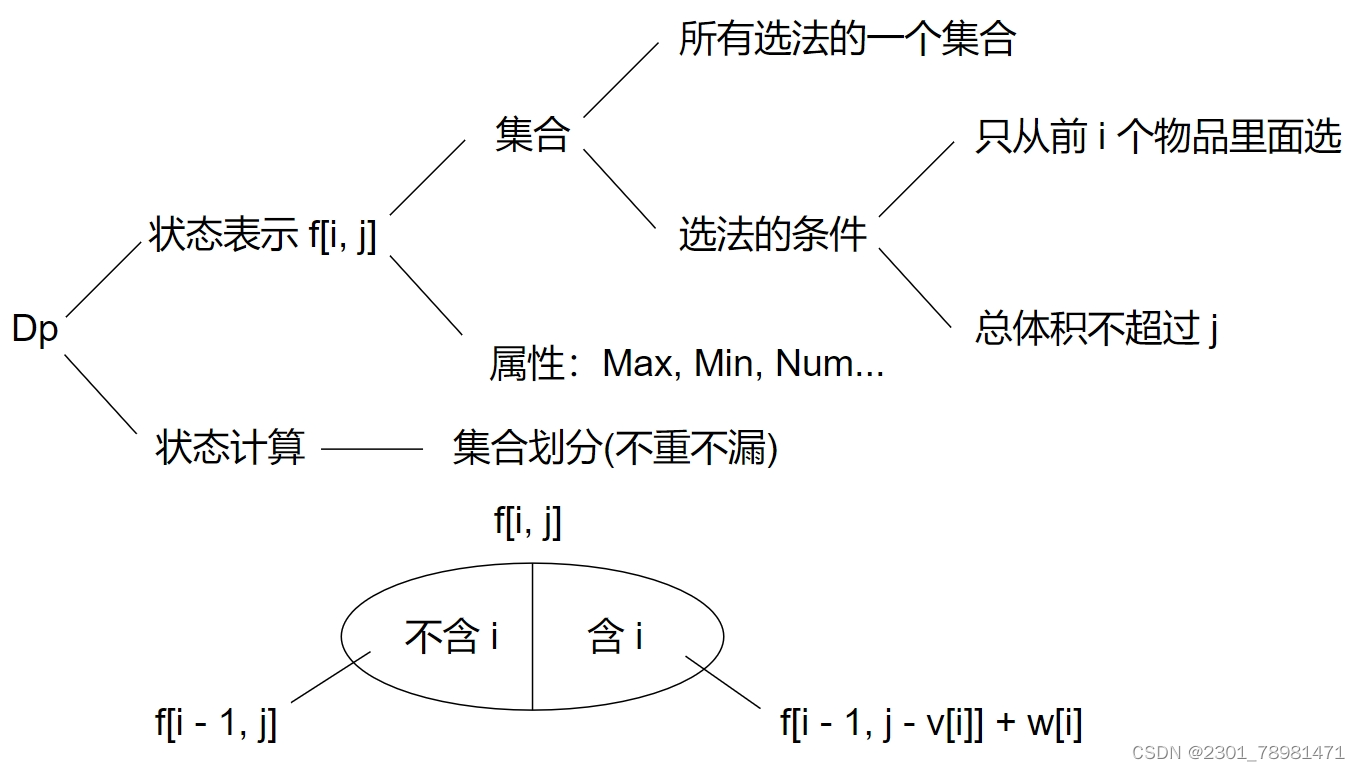
f[i, j]表示从前 $i$ 个物品里选出不超过最大容量 $j$ 的物品的最大价值总和。
可以分为两类：

不选第 $i$ 个：那么最大价值就是f[i - 1, j]，等价于上一层 => 从前 $i - 1$ 个物品里选出不超过最大容量 $j$ 的最大价值。
选第 $i$ 个：那么最大价值就是f[i - 1, j - v[i]] + w[i]，意思是在选定第 $i$ 件物品时找之前的最大价值（容量需要合法），即从前 $i - 1$ 个物品里选出最大容量不超过 $j - v [i]$ 的最大价值(需要预留空位给第 $i$ 个物品)。

由于f[i - 1][j]一定存在，而f[i - 1][j - v[i]]不一定存在，所以先将f[i][j]赋为前式。

AcWing 2. 01背包问题

题目链接：https://www.acwing.com/activity/content/problem/content/997/

CODE

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010; // 定义常量N，表示物品的最大数量
int v[N], w[N]; 	// v数组存储每个物品的体积，w数组存储每个物品的价值
int f[N][N]; 		// f数组用于动态规划，f[i][j]表示前i个物品中选择一些放入体积为j的背包能获得的最大价值

int main()
{
    int n, m; 	// n表示物品的数量，m表示背包的体积
    scanf("%d%d", &n, &m); // 从输入中读取n和m的值
    
    for(int i = 1; i <= n; ++i) cin >> v[i] >> w[i]; // 读取每个物品的体积和价值
    
    // 动态规划过程
    for(int i = 1; i <= n; ++i) // 遍历每个物品
        for(int j = 1; j <= m; ++j){ // 对于每个物品，从背包的体积开始向下遍历到物品的体积
            f[i][j] = f[i - 1][j]; // 不放入物品i
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]); 
            // 如果背包的体积大于等于物品的体积，尝试放入物品i
        }
    
    // 输出f[n][m]，即前n个物品中选择一些放入体积为m的背包能获得的最大价值
    cout << f[n][m] << endl; 
}

滚动数组优化

注意到我们状态转移时，只用到了f[i - 1, ...]来更新f[i, ...]的值，那么我们就优化掉二维数组到一维。

对于f[i, j] = f[i - 1, j] 来说，优化到一维相当于啥也没干，直接删
对于后面的一句
- 只有 $j$ 枚举到 v[i]才进行，所以for循环直接从v[i]开始往后走
- 但是我们会发现一个问题——f[i, j]是用上一层的状态来更新的，优化到一维就是用f[j - v[i]]来更新的，但是这个值由于从前往后遍历，所以这个值会被更新，那么怎么办？
  - 从后往前遍历即可。

CODE

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010; // 定义常量N，表示物品的最大数量
int v[N], w[N]; 	// v数组存储每个物品的体积，w数组存储每个物品的价值
int f[N]; 			// f数组用于动态规划，f[j]表示体积不超过j的情况下能获得的最大价值

int main()
{
    int n, m; 	// n表示物品的数量，m表示背包的体积
    scanf("%d%d", &n, &m); // 从输入中读取n和m的值
    
    for(int i = 1; i <= n; ++i) cin >> v[i] >> w[i]; // 读取每个物品的体积和价值
    
    // 动态规划过程
    for(int i = 1; i <= n; ++i) // 遍历每个物品
    	// 对于每个物品，从背包的体积开始向下遍历到物品的体积
        for(int j = m; j >= v[i]; --j){ 
            // 更新f[j]的值，选择放入物品i或者不放入物品i，取两者中的最大值
            f[j] = max(f[j], f[j - v[i]] + w[i]); 
        }
        
    cout << f[m] << endl; // 输出f[m]，即体积不超过m的情况下能获得的最大价值
}

总结

我们可以看出，其实动态规划就是把每一种可能滚了出来，然后选取符合要求的那一个解。

完全背包

介绍

与01背包类似，唯一区别就是物品数量无限。

思路

依旧是找状态转移。

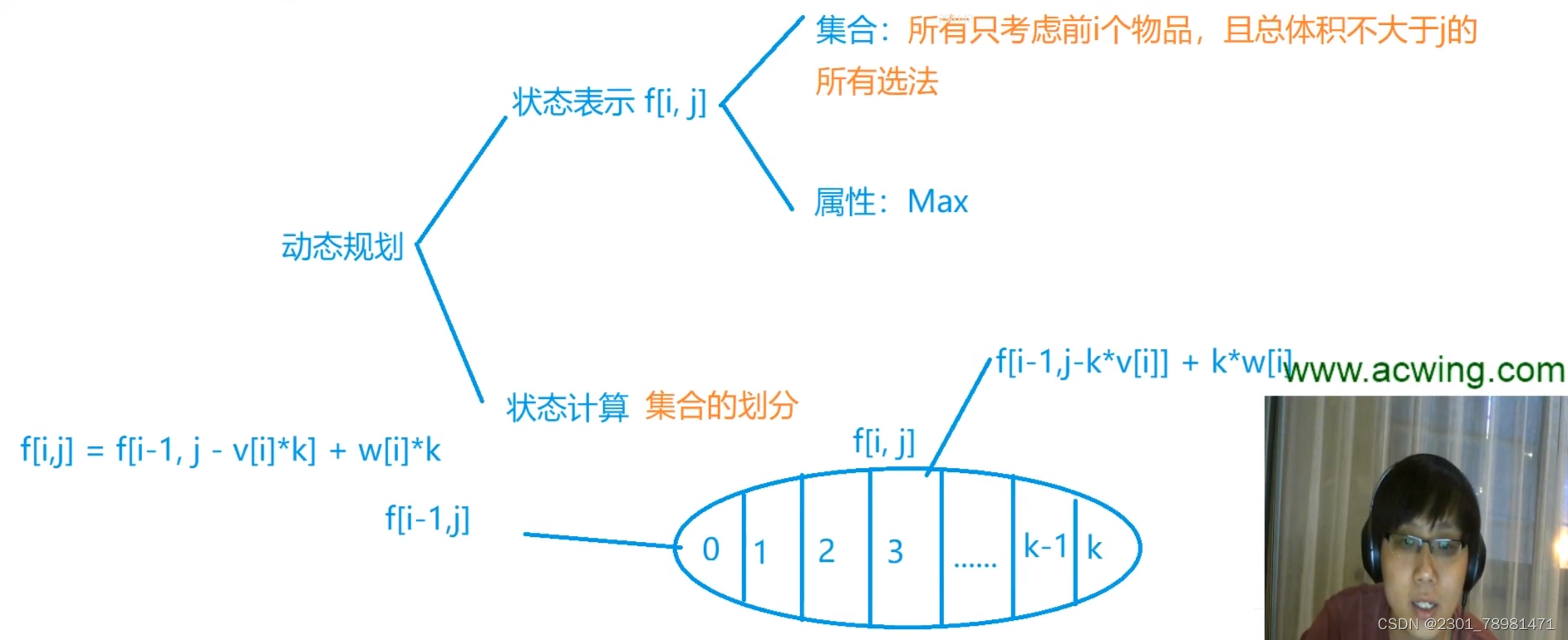
状态计算：

取 $k$ 个第 $i$ 个：从上一层中找背包容量合法的最大值。
- $k$ 范围是[0, (j / v[i])]，那么我们选其中的最大值即可。

AcWing 3. 完全背包问题

题目链接：https://www.acwing.com/activity/content/problem/content/998/

CODE

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;
int v[N], w[N];
int f[N][N];

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    
    for(int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j)
            for(int k = 0; k * v[i]<= j; ++k){
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
        }
        
    cout << f[n][m] << endl;
}

优化

我们查看这两个式子的区别：

会发现式子：f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w)
这个式子跟 $k$ 无关，那么就可以优化掉一轮循环。

CODE

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;
int v[N], w[N];
int f[N][N];

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    
    for(int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j){
            f[i][j] = f[i -1][j];
            if(v[i] <= j) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }
        
    cout << f[n][m] << endl;
}

仔细观察这段代码，发现跟01背包非常相像，唯一不同的就是01背包用的是前一层来更新当前值，而完全背包用的是当前层来更新的当前值。

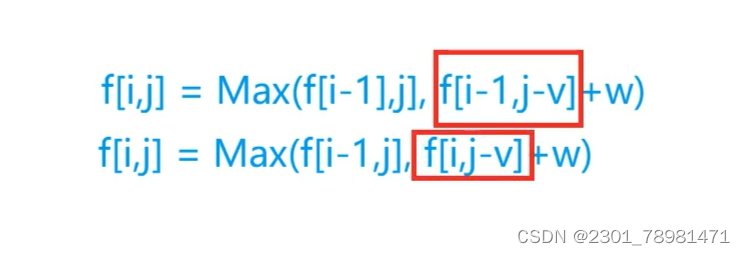
所以我们用滚动数组优化的时候不需要从后往前遍历了，因为用的就是更新后的值。

CODE

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;
int v[N], w[N];
int f[N];

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    
    for(int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; ++i)
        for(int j = v[i]; j <= m; ++j){
            if(v[i] <= j) f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
        
    cout << f[m] << endl;
}

多重背包

简介

附加条件：每件物品限制个数，且个数不一

思路

既然有个数限制，那么我就再枚举一下个数就是咯，这样时间复杂度就是： $O (v m s)$

AcWing 4. 多重背包问题

题目链接：https://www.acwing.com/activity/content/problem/content/999/

CODE

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 110;
int f[N][N];
int v[N], w[N], s[N];

int main()
{
    int n, m;
    cin >> n >> m;
    
    for(int i = 1; i <= n; ++i) cin >> v[i] >> w[i] >> s[i];
    
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j)
            for(int k = 0; k <= s[i] && k * v[i] <= j; ++k)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
                
    cout << f[n][m] << endl;
}

优化

二进制优化

时间复杂度较高，在 $n, m$ 较大的情况下过不了，那需要怎么优化呢？

我们知道，任何一个数都可以表达成二进制形式，所以可以表达为任意个 $2^k$ 的加和形式，于是我们可以将数分块封装起来：第一个箱子装 $2^0$ ，第二个箱子装 $2^1$ ，…，第 $k$ 个箱子装 $2^k$ 。那么我们可以表达的数的范围就是 $0, 2^{k + 1} - 1]$ 。

比如 $4\ ··· 3$ ，前面的三组 $2^k$ 分别装盒，剩下的不能被 $2$ 整除的放到一个箱子里。
我们可以算一下： $2^k，k∈[0, 2]$ ，能表示 $[0, 7]$ 的数据范围，那么再加上最后一个盒子，可以表示的单位就是 $[3, 10]$ ，两个合并到一起就是 $[0, 10]$ ，就是我们的要求。

像这样拆分成了多个组别，然后把它看成是01背包求解，于是乎我们就能把它压缩到一维。

完全背包的问题

为什么不用完全背包的优化思路呢？

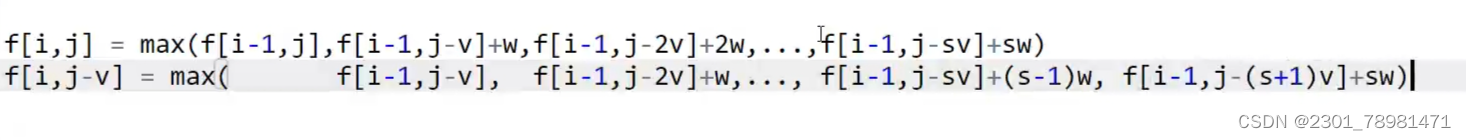
观察多重背包的状态表示方程可以看出区别于完全背包的关键点：多出了最后一项f[i - 1][j - (s + 1)v] + sw

完全背包中没有这一项，只要背包空间够用就可以一直放。
但是多重背包有限制，因为条件限制了一个物品最多有 $s$ 个

所以就不能使用完全背包的优化思路了。

AcWing 5. 多重背包问题 II

题目链接：https://www.acwing.com/activity/content/problem/content/1000/

CODE

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 11000, M = 2010;
int f[M];
int v[N], w[N];

int main()
{
    int n, m;		// 输入物品的数量和总重量
    cin >> n >> m;
    
    int cnt = 0;
    for(int i = 1; i <= n; ++i){
        int a, b, s;		// 输入每个物品的重量、价值和数量
        cin >> a >> b >> s;
        
        int k = 1;
        while(k <= s){		// 将物品分成几组
            cnt++;
            v[cnt] = k * a;
            w[cnt] = k * b;
            s -= k;
            k <<= 1;
        }
        
        if(s > 0){		// 如果还有剩余的物品，再分一组
            cnt++;
            v[cnt] = s * a;
            w[cnt] = s * b;
        }
    }
    
    for(int i = 1; i <= cnt; ++i)
        for(int j = m; j >= v[i]; --j)
            f[j] = max(f[j], f[j - v[i]] + w[i]);		// 动态规划求解
            
    cout << f[m] << endl;		// 输出结果
}

分组背包

简介

每一次选则一个组别里面的某一个元素。现在是选不选，选的话选组里面的哪个？

思路

那我再枚举一下每个组别我选哪个不就好了？
这样又被拆成了01背包，又双叒叕可以压缩到一维了。

AcWing 9. 分组背包问题

题目链接：https://www.acwing.com/activity/content/problem/content/1001/

CODE

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

// 定义物品的重量、价值和数量数组
const int N = 110;
int v[N][N], w[N][N], s[N];

// 定义动态规划的状态数组
int f[N];

int main()
{
    // 输入物品的数量和背包的总重量
    int n, m;
    cin >> n >> m;
    
    for(int i = 1; i <= n; ++i){
        // 输入每个物品的数量
        cin >> s[i];
        
        for(int j = 1; j <= s[i]; ++j){
            int a, b;
            // 输入每个物品的重量和价值
            cin >> a >> b;
            
            v[i][j] = a;
            w[i][j] = b;
        }
    }
    
    for(int i = 1; i <= n; ++i)
        for(int j = m; j > 0; --j)
            for(int k = 1; k <= s[i]; ++k)
                // 动态规划求解
                if(j >= v[i][k]) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
                
    // 输出结果
    cout << f[m] << endl;;
}

2301_78981471

关注

24
点赞
踩
18

收藏

觉得还不错? 一键收藏
0
评论
简单背包问题

01背包就是指问题：从NNN件物品中选出kkk件放入容量是VVV的背包中，最终答案具有某种属性（价值最大/最小/物品数量最多…），而且每种物品只能选一次。我们可以看出，其实动态规划就是把每一种可能滚了出来，然后选取符合要求的那一个解。与01背包类似，唯一区别就是物品数量无限。附加条件：每件物品限制个数，且个数不一每一次选则一个组别里面的某一个元素。现在是选不选，选的话选组里面的哪个？
复制链接

扫一扫