Android地图轨迹抽稀、动态绘制

废话多了，直接进入正题。

本文用到的一切地图相关的东西都来源高德地图。至于地图展示不是本文重点，所以不做赘述。文中提及的距离的计算，根据自己引用的地图类型做替换即可。文中是地图API所有会有标注。效果如如下

运动轨迹效果图

一、定位点的抽稀-道格拉斯算法

1、道格拉斯简介

Douglas一Peukcer算法由D.Douglas和T.Peueker于1973年提出，简称D一P算法，是眼下公认的线状要素化简经典算法。现有的线化简算法中，有相当一部分都是在该算法基础上进行改进产生的。它的长处是具有平移和旋转不变性，给定曲线与阂值后，抽样结果一定。

算法的基本思路是:对每一条曲线的首末点虚连一条直线,求所有点与直线的距离,并找出最大距离值dmax ,用dmax与限差D相比:若dmax < D ,这条曲线上的中间点所有舍去;若dmax ≥D ,保留dmax 相应的坐标点,并以该点为界,把曲线分为两部分,对这两部分反复使用该方法。

算法的具体过程如下:

(1) 在曲线首尾两点间虚连一条直线,求出其余各点到该直线的距离，如图3（1）。

(2) 选其最大者与阈值相比較,若大于阈值,则离该直线距离最大的点保留,否则将直线两端点间各点所有舍去，如图3（2），第4点保留。

(3) 根据所保留的点,将已知曲线分成两部分处理,反复第1、2步操作，迭代操作，即仍选距离最大者与阈值比較,依次取舍,直到无点可舍去，最后得到满足给定精度限差的曲线点坐标，如图3（3）、（4）依次保留第6点、第7点，舍去其它点,即完成线的化简。

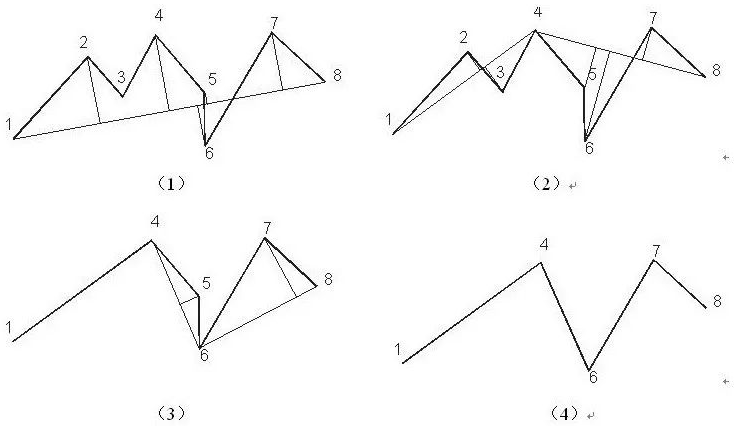
道格拉斯算法示意图

2、算法代码实现

存储经纬度坐标的实体LatLngPoint

public class LatLngPoint implements Comparable {

/**

• 用于记录每一个点的序号

*/

public int id;

/**

• 每一个点的经纬度

*/

public LatLng latLng;

public LatLngPoint(int id,LatLng latLng){

this.id = id;

this.latLng = latLng;

}

@Override

public int compareTo(@NonNull LatLngPoint o) {

if (this.id < o.id) {

return -1;

} else if (this.id > o.id)

return 1;

return 0;

}

}

使用三角形面积（使用海伦公式求得）相等方法计算点pX到点pA和pB所确定的直线的距离,

AMapUtils.calculateLineDistance(start.latLng, end.latLng)计算两点之间的距离，此公式高德API

/**

• 使用三角形面积（使用海伦公式求得）相等方法计算点pX到点pA和pB所确定的直线的距离

• @param start 起始经纬度

• @param end 结束经纬度

• @param center 前两个点之间的中心点

• @return 中心点到 start和end所在直线的距离

*/

private double distToSegment(LatLngPoint st