高精度算法之加法运算

一、话题引入

       关于加法运算，我们都一定会，但我们如果需要计算位数很高的两数相加求和的话，那就得考虑一下数据大小的限制了，我们在定义变量时变量名前都会紧跟一个数据类型，大家是否想过为什么前面需要加一个数据类型？他有什么作用呢？实际上，变量名前加一个数据类型，不仅表示了该变量的类型，还起一个限制变量数据大小的功能，关于C++中一些常见实数数据大小参见如下图：

       很明显，最大的数据类型 long long 也只 十二十个数位，如果我们需要计算位数几十位上百位的数的相加减或乘除的话，阁下应如何应对呢？

       因此，现在，我们就来聊聊关于高精度加法的算法编写！

二、话题分析

1、需求重述

    实现一个算法，能够计算位数超出基本数据类型大小的数之和，比如50位或上百位的数的和。

2、问题分析

1) 思路构建

       要计算高位数求和，按照平时的直接相加去计算的话，很明显机器无法满足我们的需求，那么我们可以换个角度去思考----->关于加法的原理是什么？

       加法加法，那还得从我们最初接触数学开始学会1+1说起，那就是小学的时候了，当时我们学的几位数的加减法的计算方法是什么呢？想必大家都知道- -> 就是竖式计算的方法。。。。额 可能同学们回一下反应不过来，没事作为一个“脆皮大学生”一下也没反应过来，那也没事，因为对于现在的我们来说这种思想已经深入意识，直接下意识的写出来了。

       好，既然让计算机去直接算行不通，那我们不妨给他加入我们人类进行加法运算的逻辑，让他使用我们的办法去算呗。如何做呢，首先举个例子，9999+9999 = 19998.

        如果我们用竖式计算相加的话，不妨写成如下图所示情形：

    大家应该很熟悉吧，这就是竖式计算加法，上下相加，逢十进一，这就是竖式计算加法的原理了。那么现在，我们就要来研究一下这种计算方式。观察此图，我们不难发现，计算的方式就是对应着各个位上的数分别从左往右进行相加，然后逢十进一给前高位。稍微理解一下，实际上他就是对各个部分做简单十位小数相加来最终得到的大数，只不过这样是得到各个位上的数，然后组成一个完整的结果。那我们不妨想想，在C++中，我们如何可以实现位上数的存放以及进行陆续的对应项加减呢？换句话说，就是要实现一个数的分解后的形式。如果确实不太理解，我再给这个竖式加以修饰，如下图所示：

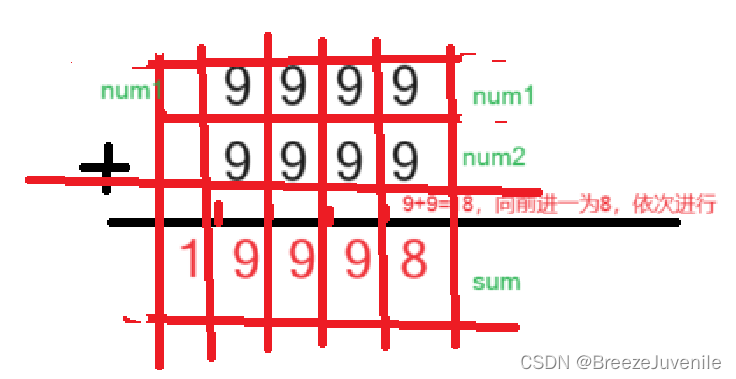
这个。。额画画方面不太擅长，大致能看出我的意思应该哈哈。所以呢看见这个竖式形式，我们应该也容易想到，使用字符数组了。

       具体做法就是，将一整个数的每一位数存放进一个字符数组中实现数字的分解，然后为实现两数各个位的相加运算，可以再把字符数组转化成整形数组进行各个位上的加法运算，最后将结果分别放进新的数组sum[]中，最后输出即可

2、思路完善与代码分解

     当然，现在我们有了大致思路，接下来就是完善一下了，因为说起来很简单，但是实际操作起来可能会出现很多复杂的情况需要进一步调整，这里，我们一遍完善一边展现小块代码的实现。

       首先我们来梳理一下，编写这个代码的核心步骤：

1、定义两个字符数组分别存放两个高位数

  首先，关于字符数组的定义，想必大家都会了，但需要注意的是，我们需要记录一下数组的长度，方便后续编码，这里，我使用了getlin()函数和str.size()函数来分别进行字符串输入和长度记录的操作。

代码实现如下：

string str1, str2;  //定义两个字符数组
getline(cin, str1);    //输入，换行即停止输入
int len1 = str1.size();  //获取字符数组长度
getline(cin, str2);
int len2 = str2.size();

2、将两个字符数组中逆序并转化成整形数组

        接着，我们要转成整形数组，然后我们再次观察竖式计算规律后容易发现，我们计算的先后顺序是从右往左进行计算的，换句话说，我们要在数组中倒着去加的话是不是会给我们有种不方便的感觉，因此，我个人想法是先把这个数字倒过来相加完以后再倒回去，这样看着更舒服，也没那么容易犯错。其次，我们要将字符数组转化成整形数组，如何转呢，这里，我介绍一种方法，就是先把字符数组中存放的每一个数字字符转化成整型数据，然后放到新定义的数组之中，具体实现方式就是对每一个字符进行 -‘0’ 操作，例如 n1[i] = str1[i] - '0' ； 即可实现转化了。

       综上所述，具体代码实现如下：< 转化+逆序 >

    //定义整形数组并初始化
	int n1[1000] = { 0 }, n2[1000] = { 0 }, sum[2000] = { 0 }, i;
    for (i = 0; i < len1; i++)  //逆序存放
	{
		n1[len1 - i - 1] = str1[i] - '0';  //数据转化，字符转化成整型
	}
	for (i = 0; i < len2; i++)
	{
		n2[len2 - i - 1] = str2[i] - '0';
	}

3、分别对应相加并将各个结果存放至另一个新的数组

    关于相加的实现，那就有一些注意的地方和讲究了，这里请仔细理解。

       首先，对应着相加，那我们想到利用for循环去遍历数组，然后实现俩数组中各个数的加法运算。那么，既然要利用循环，那么我们就需要考虑一下循环使用的条件了：

1、循环变量的初始化、循环条件、以及循环变量的更新具体怎么做？

2、循环相加时，关于实现加法求和过程中有什么需要注意的地方？

      带着这两个问题，我们来构建该块代码的具体实现思路： 

       第一个，我们假设循环变量为i，循环变量的更新也很简单，即i++；重点就在于这个循环条件：因为这个循环是为了将各个位的和放进一个新的数组中存放，所以我们要思考一下这个数组要多大空间。关于这个空间的大小，首先两数相加以后的结果的位数肯定不会比两加数的位数小，换句话说，如果是1+1，则结果是一位，12+1，结果是两位......以此类推，两数相加的结果的位数一定至少是两数中位数最大的一个，即如果加数是123 87，两者最多是三位数，那么和也一定最少也是三位数，那么有没有可能是四位数或者更高位数呢？答案是有可能高有且仅高一位，即当两数之和的最高位相加发生进位时，和数会多出一位来。

       因此，综上可知这个循环条件，即表达和数的数组长度，换句话说，就是和数的最多位数就是两个加数中位数最高的位数+1即可，而加数的位数就是存放量加数的数组长度，所以，首先比较两数组长度找出最大的那个然后+1得到的长度即可作为和数的数组长度，具体实现如下：

    int maxlen = len1+1; //粗略确定和数的数组长度maxlen
	len1 < len2 ? maxlen = len2 + 1 : maxlen = len1 + 1;

       第二，循环要素确定完了，接下来就是确定循环体中的内容了，即加法的实现。前面说到，加法就是把两个数组对应的位上的数相加，但是这里我们要注意的是关于进位的处理。这里，我们一步一步慢慢思考：

       首先，要处理进位的问题，我们思考，满足什么条件就会发生进位、如果发生了进位，那么结果又会变成什么样子？    很明显，当相加得到的和大于10以后就会发生进位，然后进位后会向前进一，然后原位上的数就会少10，（就比如 8+8 ，得到16，大于10了，向前进一，原位上就减10，变成了6，前一位就是从0变成了1，拼接起来的过程不妨画图理解），如下图所示：

       由此看出，两数的加法以及发生的进位处理，需要细分出具体的过程，进位数可以通过除10得到，而进位后原位上的数可以用取余得到，这个时候，我们最好用一个变量flag(可自定义名字，这里我直接用flag表示进位数)存放进位数，然后起初无进位，所以默认为0，即初始化int flag = 0; ，然后如果一个多位数个位进位以后，那么前一位会+1，然后原位要取余得到进位后的数，即n1+n2+flag;flag = n1+n2/10;n1+n1%10，这就是是每一次循环要做的事。

具体代码实现如下：

int flag = 0;  //进位数，起初默认为0
	for (i = 0; i < maxlen; i++)
	{
		若两个相加大于10，需要判断进位情况，%10判断
		sum[i] += n1[i] + n2[i]+flag;  //每一次相加都会额外加上上一位的进位数
//第一次相加时进位默认位0，因为第一次相加时无上一次进位
		flag = sum[i] / 10;  //相加以后进位的数
		sum[i] %= 10;  //进位以后原位上的数
	}

4、处理特殊情况，确定最终和数位数

       前面，我们经循环后得出了最终的求和结果，但是当时选取的结果的位数属于最大情况，即有可能两数相加以后最高位并没有发生进位，如123+123 此时我们给结果的位数确定在3+1=4位，但是最后结果是246只有三位数，那么最后和的数组是放的 6 4 2 0  （期初我们对数组的定义都进行了初始化操作，在未后续进行赋值的情况下数组内存放的均为0，且说了为了相加方便我们采用逆序数组求得和），那么最终倒过来输出的时候会显示 0246，这显得不太好看，因为平时算加法不为在前面多个0。

       因此，这里我们还需要做一个判断，如果和数的数组的最后一位空着了即为0时，则清掉这个空间，也就是让数组大小-1就行，一般来说只需要减一次即可。

       具体代码实现如下：

//如果最高位没有进位填补，即仍为0，则我们需要清掉这个空间，避免输出最高位为0的情况
	if (sum[maxlen - 1] == 0 && maxlen > 0)	maxlen--;

5、结果输出，完结撒花

     最后，我们就可以对结果进行输出了，注意，此时结果是倒着的，因此输出时我们要进行逆序输出：即i=0,我们输出第maxlen-1-i个数。

具体操作如下：

	//4、最后逆序输出最终的数组即可
    for (int i = 0; i < maxlen; i++)
	{
		cout << sum[maxlen - 1 - i];
	}

 6、注意事项

头文件引入 --> 使用了 getline()函数以及string类型等等，需要引入string头文件;

相关变量的初始化 --> 记得定义的整形数组的初始化。

三、总代码实现

以下是C++实现：

#include<iostream>
#include<string>
using namespace std;
//高精度加法

int main()
{
	//1、利用两个字符数组分别存放两个高位数
	string str1, str2;
	int n1[1000] = { 0 }, n2[1000] = { 0 }, sum[2000] = { 0 }, i;
	getline(cin, str1);
	int len1 = str1.size();
	getline(cin, str2);
	int len2 = str2.size();

	//2、将两个字符数组中逆序并转化成整形数组
	for (i = 0; i < len1; i++)
	{
		n1[len1 - i - 1] = str1[i] - '0';
	}
	for (i = 0; i < len2; i++)
	{
		n2[len2 - i - 1] = str2[i] - '0';
	}
	
	//两数之和的位数最高是两者最大值+1，比如999 + 999 =1998 最多有四位
	//因此这里我们需要判断一下
	int maxlen = len1+1;
	len1 < len2 ? maxlen = len2 + 1 : maxlen = len1 + 1;

	//3、分别对应相加后将各个结果存放至领一个新的数组
	int flag = 0;
	for (i = 0; i < maxlen; i++)
	{
		//1 若两个相加大于10，需要判断进位情况，%10判断
		sum[i] += n1[i] + n2[i]+flag;
		flag = sum[i] / 10;
		sum[i] %= 10;
	}
	//如果最高位没有进位填补，即仍为0，则我们需要清掉这个空间，避免输出最高位为0的情况
	if (sum[maxlen - 1] == 0 && maxlen > 0)	maxlen--;

	//4、最后逆序输出最终的数组即可
	for (int i = 0; i < maxlen; i++)
	{
		cout << sum[maxlen - 1 - i];
	}
	return 0;
}

       以上就是我对高精度加法的一些想法的叙述了，如有哪些表述不清，可在评论区反馈，我以后多多改进，争取叙述更加清楚明白，谢谢！