Introduction to Modern Cryptography-数论基础篇

FansMing1

已于 2023-11-26 17:11:32 修改

阅读量154

点赞数

分类专栏：现代密码学导论文章标签：算法学习密码学

于 2023-10-31 09:50:55 首次发布

本文链接：https://blog.csdn.net/2301_79553633/article/details/134060382

版权

现代密码学导论专栏收录该内容

10 篇文章 1 订阅

订阅专栏

现代密码学中用到了很多基础数论中的结论，特别是公钥加密体系（例如RSA算法，椭圆曲线加密等）。本文目的在于梳理现代密码学中常用到的基础数论方面的定理和结论。了解这些知识，应该能够理解现代密码学中经典的Diffie-Hellman密钥协商和RSA算法的原理，进而能够理解秘钥管理、数字签名、消息认证、公钥证书等密码学领域的问题。

互质和整除

整除的定义：设 a,b∈Z , a≠0。如果 $\exists q\in Z$ ,使得 $b=aq$ ,那么就说 b可被a整除，记作 $a\mid b$ 。

约数（因数）：若 $a\mid b$ ，则称b是a的倍数，a是b的约数。

$\bullet$ d整除a记作： $d\mid a$ ; 如果 $d\mid a$ 且 $d\mid b$ ，那么 $d\mid \left ( ax+by \right )$

$\bullet$ 如果p是素数，且 $p\mid ab$ ，则 $p\mid a$ 或者 $p\mid b$

$\bullet$ 1和任意一个自然数是都是互质关系

$\bullet$ 任意两个质数构成互质关系

$\bullet$ 一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如3和10

$\bullet$ 如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如97和57

$\bullet$ p是大于1的整数，则p和p−1构成互质关系，比如57和56

$\bullet$ p是大于1的奇数，则p和p−2构成互质关系，比如17和15

$\bullet$ 素数p与1到p−1的任意整数均互质。并且阶乘(p−1)!与p互质(这个结论在费马小定理和欧拉定理的证明过程中会用到)

欧几里德算法

(GCD递归定理) ：对于任意的非负整数a和正整数b，满足

$gcd\left ( a,b \right )= gcd\left ( b,a \mod b \right )$

其计算流程：

$r_{n}$ 即为求得的a和b的最大公约数

参考：欧几里得算法

扩展欧几里德算法

扩展欧几里德算法可以用来求解一类有意思的线性方程的整数解，该线性方程的整数求解过程与最大公约数有密切关系。

对于线性方程（a,b,c为常数）： $ax+by=c$ 是很熟悉的方程。

这里讨论情况是a,b,c满足一定的关系： $c=gcd(a,b)$ ，也即是这样的线性方程：

$ax+by=gcd(a,b)$

这个线性方程必然有整数解，该算法利用欧几里德算法求解最大公约数过程中的中间商和余数，进行扩展运算，在求 $gcd(a,b)$ 的过程中，同时也就求得线性方程的整数解 $\left ( x,y \right )$ 。

参考：扩展欧几里得算法

算术基本定理

(算术基本定理)：每个整数 $n\geqslant 2$ 可唯一分解成素数的乘积： $n= p_{1}^{e_{1}}p_{2}^{e_{2}}\cdot \cdot \cdot p_{r}^{e_{r}}$

其中， $p_{i}$ 为素数，且 $p_{1}< p_{2}< \cdot \cdot \cdot < p_{r}$ ， $e_{i}$ 为正整数。

实际上，看似理所当然的事实，其实并非如此。如果自定义一个有别正整数集合的其他集合，很可能就不再满足唯一分解定理。例如，集合E是由偶数构成的集合：E={0,2,4,6,8,10,12...}

也可在这个集合中定义所谓的“素数”，称之为“E-素数”，2,6,10,14,18,22,26,30都是“E-素数”。对这个集合中的元素尝试做“素因子”分解，并不总是能唯一分解,例如，180=10x18=2x30，存在两种“E-素数”的分解形式。

实际上算术基本定理包含两个方面：

1） $n$ 可以分解成素数乘积的形式。

2）仅有一种这样的素因子分解的形式（当然这里不考虑因数重排序的情况）。

显然唯一性分解是算术基本定理的关键和重点。

另外一个有意思的事实：若n为合数，则在小于等于 $\sqrt{n}$ 的数中必定有一个数 $a$ 整除合数 $n$ 。

该结论基于算术基本定理：合数 $n$ 必定可以唯一分解多个素数的乘积，这里假设 p 是它的素因子中最小的一个，则n必定可以写成 $n=p\times m$ 的形式，这里的m是其余大于等于 p 的素因子的乘积，显然 $m\geqslant p$ ,因此 $n= p\times m\geq p\times p=p ^{2}$

所以，在 $0\cdot \cdot \cdot \sqrt{n}$ 的范围内，必定存在一个数 $a$ 整除 $n$ 。

可以利用这种方法简单的分辨一个数是否是素数，也可以反复执行上述过程将一个较小的合数进行素因子分解。

同余式与模算术

一般来讲，可以将 mod 视为一种求余数的二元运算符，例如2=5mod3；也可以用来表示同

余关系，这种同余关系通常用同余式表示。例如2≡5(mod3)表示模3时2与5同余。

基本模运算：

（1）若a≡b(mod m)，c≡d(mod m)，则a±c≡b±d(mod m)；

（2）若a≡b(mod m)，c≡d(mod m)，则a×c≡b×d(mod m)；

（3）若a≡b(mod m)，且n∈N，则an≡bn(mod m)；

（4）若a≡b(mod m)，且k是整数，则k×a≡k×b(mod m)；

（5）若a≡b(mod m)，且m＝qn，则a≡b(mod n)，a≡b(mod q)。

同余式虽然有别于普通的算数运算下的等式，但是具有相同模的同余式与普通等式有一些相似的特性：

$\bullet$ 如果已知： $a_{1}\equiv b _{1}\left (mod\ m\right )$ 且 $a_{2}\equiv b _{2}\left (mod\ m\right )$

那么有： $a_{1}\pm a _{2}\equiv b_{1}\pm b _{2}\left ( mod\ m \right )$ 和 $a_{1} a _{2}\equiv b_{1}b _{2}\left ( mod\ m \right )$

$\bullet$ 如果 $a^{k}\equiv b\left ( mod\ m \right )$ ，那么， $\left ( a^{k} \right )^{j} \equiv b^{j}\left ( mod\ m \right )$

特别的当 $b= 1$ 时：如果 $a^{k}\equiv 1\left ( mod\ m \right )$ ，那么， $\left ( a^{k} \right )^{j} \equiv 1\left ( mod\ m \right )$

但是，由 $ac\equiv bc\left ( mod\ m \right )$ 不一定能得到 $a\equiv b\left ( mod\ m \right )$

例如 $2\times 25\equiv 2\times 20\left ( mod\ 10 \right )$ ，但是 $25\not\equiv 20\left ( mod\ 10 \right )$

只有当c和m互质时（也即是 $gcd=( c,m )= 1$ ），才能够从同余式两边消去c。

由同余式可以引出同余方程： $ax\equiv c\left ( mod\ m \right )$

求解上述同余方程有一个定理，叫做同余方程定理。

(同余方程定理)：设a,c,m是整数， $m\geqslant 1$ ，且设 $g= gcd\left ( a,m \right )$ ，则

1）如果g不整除c，那么同余方程 $ax\equiv c\left ( mod\ m \right )$ 没有解。

2）如果g整除c，那么同余方程 $ax\equiv c\left ( mod\ m \right )$ 恰好有 $g$ 个解。

以上同余方程的求解过程需要用到扩展欧几里德的求解方法。实际上 $ax\equiv c\left ( mod\ m \right )$ 可以转化为线性方程 $ax+m(-y)=c$ 。

特别地，当a和m互质，即 $g= gcd\left ( a,m \right )= 1$ 时，同余方程变成： $ax\equiv 1\left ( mod\ m \right )$

$a$ 和 $x$ 互为模反元素，这在RSA公钥加密算法生成秘钥过程中有应用。

剩余系

所谓“剩余系”，就是指对于某一个特定的正整数n，一个整数集中的数模n所得的余数域。

如果一个剩余系中包含了这个正整数所有可能的余数（一般地，对于任意正整数n，有n个余数：0,1,2,...,n-1），那么就被称为是模n的一个完全剩余系。

简化剩余系(reduced residue system)也称既约剩余系或缩系，是m的完全剩余系中与m互素的数构成的子集，如果模m的一个剩余类里所有数都与m互素，就把它叫做与模m互素的剩余类。在与模m互素的全体剩余类中，从每一个类中各任取一个数作为代表组成的集合，叫做模m的一个简化剩余系。例如，模5的一个简化剩余系是1，2，3，4，模10的一个简化剩余系是1，3，7，9，模18的一个简化剩余系是1，5，7，11，13，17。

费马小定理

费马小定理揭示了整数的幂在模运算下的特殊规律。

(费马小定理)：设p是素数，a是任意的正整数且满足，则 $a^{p-1}\equiv 1\left ( mod\ p \right )$

实际上对于条件的更简单的表述可以为" $a$ 与素数 $p$ 互质"即可。

证明费马小定理并不是非常难，证明过程是基于这样一个结论：

设素数 $p$ 与任意正整数 $a$ 互质，那么集合 $S= \left \{ a,2a,3a,\cdot \cdot \cdot \left ( p-1 \right ) a\right \}$ 中任意任意两个元素均不可能模 $p$ 同余。也即是 $ja\not\equiv ka\left ( mod\ p \right )$ 。其证明过程只需要利用反证法即可。

上述结论表明：

如果对集合 $S$ 中的每一个元素模p的结果，其结果刚好与集合 $T= \left \{ 1,2,3,4\cdot \cdot \cdot \left ( p-1 \right ) \right \}$ 中的元素一一对应（不考虑次序重排）。

于是有： $a\times 2a\times 3a\cdot \cdot \cdot \times \left ( p-1 \right )a\equiv 1\times 2\times 3\cdot \cdot \cdot \left ( p-1 \right )\left ( mod\ p \right )$

整理得： $\left ( p-1 \right )!\times a^{p-1}\equiv \left ( p-1 \right )!\left ( mod\ p \right )$

这里必然满足 $gcd((p-1)!\ ,\ p)=1$ ，所以，可以两边消去 $\left ( p-1 \right )!$ ，得到 $a^{p-1}\equiv 1\left ( mod\ p \right )$

正是由于存在这样的关系，所有费马小定理可以用来简化对整数的幂取模的计算。

费马小定理在数论中非常重要，与其三个定理（分别是威尔逊定理、欧拉定理和中国剩余定理）合称数论四大基本定理。更有趣的是，费马小定理实际上可以视为欧拉定理的一个特例。

最后，费马小定理还有一种等价的表示形式：

若p是素数，a是正整数，则 $a^{p-1}\equiv a\left ( mod\ p \right )$

这里不需要a与p互质的条件。这并不是一件很奇怪的事情，无非是利用模算术的除法特性（见同余式与模算术）的变形。

中国剩余定理

中国剩余定理（也叫作孙子定理）所描述的问题在小学课本中都能找到，只不过当时只能用方程组去刻画这个的问题。

在数论中，它有不止一种表述形式，其中一种比较易懂的描述为：

设m,n是正整数， $gcd\left ( m,n \right )= 1$ ，b,c是任意正整数，则同余方程组

$x\equiv b\left ( mod\ m \right )$

$x\equiv c\left ( mod\ n \right )$
恰有一个解 $0\leqslant x\leqslant mn$

以上是从方程的角度描述，另外一种从对应的角度(数与k元组的对应关系)表述也是可行的，可以看做是上面表述形式更抽象的扩展：

令 $M= \prod _{i=1}^{k}m_{i}$ ，其中 $m_{i}$ 两两互质

则 $Z_{M}= \left \{ 0,1,2,3\cdot \cdot \cdot \left ( m-1 \right ) \right \}$ 中任意整数会对应一个k元组：

$A\leftrightarrow \left ( a_{1},a_{2},\cdot \cdot \cdot a_{k} \right )$

其中 $a_{i}$ 当然是要在 $Z_{m_{i}}$ 中(也即是 $a_{i}\in Z_{m_{i}}$ )，并且ai由关系 $a_{i}= A\ mod\ m_{i}$ 给出。

从以上定理实际上可以推断出 A 与 k 元组唯一一对应的事实。

参考：中国剩余定理

欧拉函数与欧拉定理

欧拉函数 $\phi \left ( m \right )$ 的含义是1到m−1中（也就是[1,m−1]）且与m互质的整数的个数。它是数论中一个非常重要的函数。

如何计算欧拉函数的值是一个关键的问题。欧拉函数的计算方法的推导主要用到两个结论：

（1）如果 $p$ 是素数， $k\geqslant 1$ ，则 $\phi \left ( p^{k} \right )= p^{k}-p^{k-1}= p^{k}\left ( 1-\frac{1}{p} \right )$

（2）如果 $gcd\left ( m,n \right )= 1$ ，则 $\phi \left ( mn \right )=\phi \left ( m \right )\times \phi \left ( n \right )$

欧拉定理与费马小定理同样都是揭示了整数的幂在模运算下的特殊规律，实际上他们有微妙的关系。

(欧拉定理)：如果 $gcd(a,m)=1$ ，则 $a^{\phi \left ( m \right )}\equiv 1\left ( mod\ m \right )$

欧拉定理与费马小定理有微妙的关系：如果这里的m是一个素数，则 $\phi (m)= m-1$ ，由此得到费马小定理。说明费马小定理实际上可以看成欧拉定理的一个特例。

与费马小定理类似，欧拉定理也有另外一种表现形式：

$a^{\phi \left ( m \right )+1}\equiv a\left ( mod\ m \right )$

这里没有要求a与m互质的条件

欧拉定理的证明

模反元素

如果两个正整数a,b和m互质，那么一定可以找到整数b，使得 ab−1 被m整除，或者说ab被m除的余数是1。

$ab\equiv 1\left ( mod\ m \right )$

则此时b就是a的模反元素。

实际上这里相当于求解同余方程 $ax\equiv 1\left ( mod\ m \right )$ ，当 $gcd(a,m)=1$ 时，必定存在一个整数解，因此模反元素必定存在，此解即是a的模反元素。

从欧拉定理的角度

$a^{\phi \left ( m \right )}= a\times a^{\phi (m)-1}\equiv 1\left ( mod\ m \right )$

也可以证明模反元素是存在的。

更进一步，如果p是素数，由集合 $Z_{p}= \left \{ 0,1,2,\cdot \cdot \cdot p-1 \right \}$ 和二元运算模p的算术运算构成一个有限交换群G。G中每一个元素都有乘法逆元，此乘法逆元就是这里的模反元素。

本原根

本原根通常与幂模有关，观察如下例子：

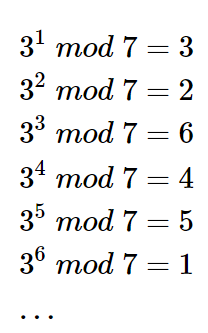
可以发现3的各幂次模n能够得到一个循环的序列{3,2,6,4,5,1}，这个序列刚好对应着小于等于7且与7互质的整数集合。这并非一个偶然规律，2或者3的各次幂模5，2或者6或者7或者8的各次幂模11都能够得到同样的规律。

当然也并不是总是这样，例如

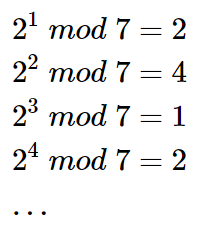
更一般的，考虑p为素数， $gcd(a,p)=1$ 且 $a \leqslant p-1$ ，如下序列

$a\ mod\ p,a^{2}\ mod\ p,a^{3}\ mod\ p,\cdot \cdot \cdot ,a^{p-3}\ mod\ p,a^{p-2}\ mod\ p,a^{p-1}\ mod\ p$

如果 $a^{p-1}\ mod\ p= 1$ ，那么可以证明上述序列值必然各不相同（证明可以用反证法，不存在 $a^{i} \equiv a^{j} (mod\ p)$ 的情况）。因为这里模p运算的结果总会映射到集合Zp={1,2,3,...,p−2,p−1}，这个集合中的每个元素与p互质。也即是说不考虑次序重排，上述序列值对应了集合Zp的值。