映射、等价关系
有序对
有序对 (ordered pair) ,它满足性质
这个有序对的概念涉及两个对象,首先,它是“对”,包含两个特定的元素a和b,其次,它有序。
若,则
数学中除集合以外的一切定义,都可以由集合给出。还可以这样的定义:
关系
二元关系 (binary relation)是一个非空集合,它的元素都是有序对。二元关系简称“关系”
空集也是特殊的二元关系
我们常将一个二元关系记作R,(注意到R是一个集合),如果 <a,b>∈R ,则记作 aRb
记集合 {a|∃b(aRb)} 为R的 定义域 ,集合 {b|∃a(aRb)} 为R的 值域
有了关系的定义,我们一般怎样构造一个关系呢?
我们可以定义两个集合的直积或笛卡尔乘积(Cartesian product):A×B={<a,b>|a∈A∧b∈B}
A×B的任何子集也是关系,而 对于任意 A×B 的子集 ,我们称其为“从A到B的关系”,若A=B,则称为“A上的关系”
我们有两个对象,他们之间可能有先后顺序,可能有主次矛盾,而关系,则是将这些性质数学化的手段。我们常见的二元关系,有之前讲的集合之间的包含与被包含关系,也有数之间的大小关系。
设R为集合A上的关系
如果 ∀x(x∈A→xRx) ,则称R为 自反的 (reflexive)
如果 ∀x(x∈A→¬xRx) ,则称R为 反自反的 (irreflexive)
如果 ∀x∀y(x,y∈A∧xRy→yRx) ,则称R为 对称的 (symmetric)
如果 ∀x∀y(x,y∈A∧xRy∧yRx→x=y) ,则称R为 反对称的 (antisymmetric)
如果 ∀x∀y∀z(x,y,z∈A∧xRy∧yRz→xRz) ,则称R为 传递的 (transitive)
用自然的语言来说
如果所有x和自身都有关系R,则R为自反的;
如果所有x和自身都没有关系R,则R为反自反的;
如果x和y有关系R,那么y和x也有关系R,则R为对称的;
如果x和y有关系R,那么y和x就没有关系R,则R为反对称的;
如果x和y,y和z有关系R,那么x和z有关系R,则R为传递的;
数之间的小于关系是反自反的,传递的;小于等于关系是自反的,反对称的,传递的;相等关系是自反的,对称的,反对称的,传递的。
映射
由关系我们引入数学上分布最广的对象—— 函数 (function),亦即, 映射 (mapping)。映射是一种特殊的二元关系。
设F为二元关系,A、B为其定义域、值域,若 ∀x∈A , ∃唯一 y∈B ,使得 xFy ,则称F为映射,并记 y=f(x) 。
这里的定义与二元关系的区别就在于“唯一”。注意:这里的映射也是一个集合。
如果映射F的定义域为A,值域包含于B,则称f为由A到B的映射,B称为其陪域 (codomain)
映射有三个自身的属性——定义域、对应关系与陪域。
“由A到B的映射”可知,B不是由A和F唯一确定的,只要包含F值域的集合,都可称之为“由A到B的映射”。
映射的表示方法:
如:映射 f:x→2x,x∈[1,2]是严格的映射的表示方法。
注意到映射的表示中,全无等号的出现。第一个冒号,意在诠释这个映射 f 。如果映射f后接等号,那也只能用集合或另一个映射去与之相等,如 f={<1,2>,<2,2>,<3,6>} ;第二个箭头,意在区别哪个是定义域的元素,哪个是值域的元素,在计算机语言中,有时也可以用等号, 2x=x2
此外,由A到B的映射F还可记为 F:A→B
比如说, f:x→2x,x∈[1,2] 可记作 F:[1,2]→[2,4] ,亦可记作F:[1,2]→R ,其中, [2,4][2,4] 和 R 均为F的陪域,而只有 [2,4][2,4] 为其值域。
映射的分类:
设F为由A到B的映射
如果F的值域为B,则称F为 满射 (surjective)
如果 ∀x∀y(x≠y→f(x)≠f(y)) ,则称F为 单射 (injective)
如果F既是满射也是单射,则称F为 双射 (bijective)
群
我们在 “映射” 的中定义了二元运算为 A×B→C, 如果A=B=C, 即一个集合中的任意两个元素运算后的结果仍然在这个集合中, 那么我们说这个二元运算是封闭的。 二元运算的符号可以任意决定,如果使用 ⋅ 作为运算符,那么二元运算就可以简单写为 a⋅b=c 。 注意,这里的 ⋅ 只是表示某一个运算,不一定是我们通常的乘法或点乘运算。
群的基本定义
群:给定一个集合 G={a,b,c...} 和集合上的二元运算 " ⋅ ",要求满足下面四个条件:
①封闭性:对于任意a,b∈G,一定存在c∈G,使得a⋅b=c
②结合律:对于任意a,b,c∈G,有(a⋅b)⋅c=a⋅(b⋅c)
③单位元:存在e∈G,使得对任意a∈G,有 a⋅e=e⋅a=a
④逆元:对任意a∈G,均存在b∈G,使得a⋅b=e,其中b称作a的逆元,记作
如果一个集合满足这个条件,那么就称这个集合是在运算 ·下的一个群
上述定义中,第③条中的元素 e 称为单位元,第④条中的 b 称为 a 的逆元,通常记作 。成立①的集合 G 称为原群;成立①②的集合 G 称为半群(semigroup);成立①②③的集合 G 称为幺半群(monoid)。全体正整数对于整数加法构成半群,全体自然数对于整数加法构成幺半群,全体整数对于整数加法构成群。
阿贝尔群
如果一个群 G 中的任意两个元素 a,b 都满足 ab=ba ,则该群称为交换群或Abel群。
![]()
群的基本性质
①一个群的单位元是唯一的
②群中任意元素的逆元是唯一的
③对a,b,c∈G,若a⋅b=a⋅c,则b=c
④若G是一个群,且a∈G满足a⋅a=a,那么a=e
⑤对任意a∈G,有 ,a⋅e=a
子群
设G是一个群,H是G的一个子集,且H在相同意义下仍然构成一个群,则称H是G的一个子群
平凡子群:任一群G都有两个明显的子群,称为G的平凡子群。
由其单位元素组成的子群{1},称为G的单位子群;G本身,其余的子群称为非平凡子群。
显然:群G有两个平凡子群:G,H={e}(e表示单位元)。如果其他的子群存在的话,称为非平凡子群,若子群H≠G,称为真子群,记为H<G.
子群的性质
设 H≤G ,则 H 的单位元就是 G 的单位元,H 的元在H 中的逆元就是它在 G 中的逆元。

子群的判定定理
设H是群G的一个非空子集,则H是群G的子群的充分必要条件为:
证明:
充分性
因为H和G上的运算是相同的,所以不必再证明H上的运算的是否满足结合律
∵群G的单位元也是群H的单位元
∴e∈H,即H有单位元
又∵对于e∈H,∀a∈H有,a−1=ea−1∈H(假设条件)
∴∀a∈H,a−1∈H即H中的每个元素都有逆元
所以H是G的子群
必要性
若H是一个群,则∀b∈H,b−1∈H
又由群的运算封闭性可知∀a∈H,ab−1∈H
子群的构造
给定一个群,如何构造其子群呢?下面是一个构造子群的例子。
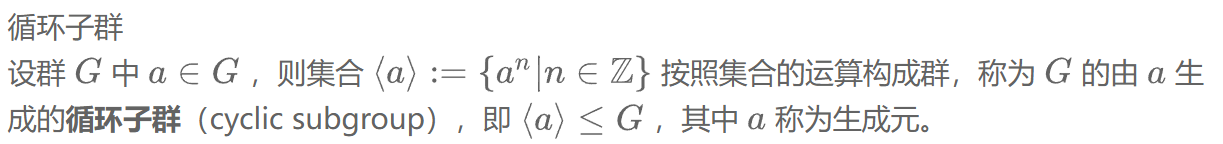
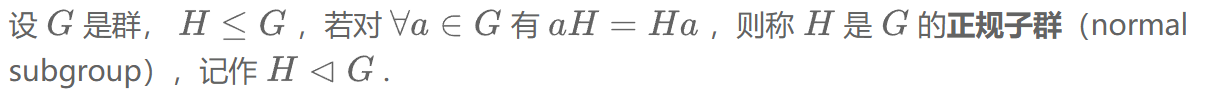
循环群的子群都是循环群。(循环群结构定理)
交换群的子群都是交换群。(显然)
商集
商集的定义:设H是群G的子群,则H在G中不同左陪集组成的新集合{aH|a∈G},叫做H在G中的商集,记作G/H,即G/H={aH|a∈G}而G/H中不同左陪集的个数叫做H在G中的指标,记为[G:H]
商集指标的性质:设H是群G的子群,则|G|=[G:H]|H|更进一步,如果K,H是群G的子群,且K是H的子群,则[G:K]=[G:H][H:K],其中的每个指标都是有限的
拉格朗日推论:设H是有限群G的子群,则子群的阶|H|是群G的阶|G|的因数
Lagrange定理

该定理可以证明很多重要的推论。例如我们可以知道一个10阶群不会有 6 阶子群,其非平凡子群的阶数只可能是2和5。我们还可以用Lagrange定理证明“元素的阶整除群的阶”这一结论。
素数阶群都是循环群






















 3543
3543











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








