机器学习｜逻辑回归

最新推荐文章于 2024-05-28 18:15:56 发布

I0420AY

最新推荐文章于 2024-05-28 18:15:56 发布

阅读量1.6k

点赞数 24

文章标签：机器学习逻辑回归人工智能

本文链接：https://blog.csdn.net/2301_79617030/article/details/139220030

版权

一、逻辑回归（Logistic回归）

1、逻辑回归介绍

逻辑回归是一个分类的算法，它基于多元线性回归，正因如此，逻辑回归这个分类算法是线性的分类器。

逻辑回归中对应一条非常重要的曲线S型曲线，其对应的函数是Sigmoid函数：

$f(x)=\frac{1}{1+e^{-x}}$

它有一个非常棒的特性，其导数可以用其自身表示：

${f}'(x)=\frac{e^{-x}}{(1+e^{-x})^{2}}=f(x)*\frac{1+e^{-x}-1}{1+e^{-x}}=f(x)(1-f(x))$

import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
    return 1/(1+np.exp(-x))
x=np.linspace(-5,5,100)
y=sigmoid(x)
plt.plot(x,y,color='green')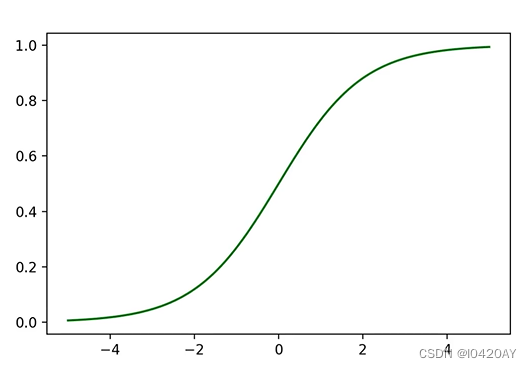

图1 sigmoid曲线

2、Sigmoid函数介绍

逻辑回归就是在多元线性回归基础上把结果缩放到0~1之间。 $h_{\theta }(x)$ 越接近1越是正例， $h_{\theta }(x)$ 越接近0越是负例，根据中间 0.5 将数据分为二类。其中 $h_{\theta }(x)$ 就是概率函数：

$h_{\theta }(x)=g(\theta ^{T}x)=\frac{1}{1+e^{-\theta ^{T}x}}$

我们知道分类器的本质就是要找到分界，所以当我们把0.5作为分类边界时，我们要找的就是
$\hat{y}=h_{\theta }(x)=\frac{1}{1+e^{-\theta ^{T}x}}=0.5$ ，即 $z=\theta ^{T}x=0$ 时， $\theta$ 的解。

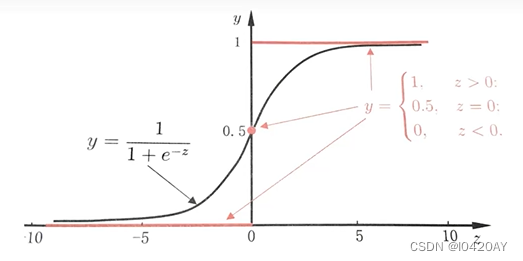
图2 单位阶跃函数与对数几率函数

求解过程如下：

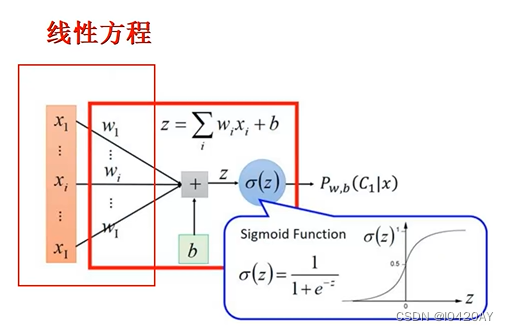
二分类有个特点就是正例的概率+负例的概率=1。一个非常简单的试验是只有两种可能结果的试验，比如正面或反面，成功或失败等等。为方便起见，记这两个可能的结果为0和1，下面的定义就是建立在这类试验基础之上的。如果随机变量x只取0和1两个值，并且相应的概率为:

$P_{r}(x=1)=p;P_{r}(x=0)=1-p;0<p<1$

则称随机变量x服从参数为p的Bernouli伯努利分布(0-1分布)，则x的概率函数可写:

$f(x|p)=\begin{cases} p^{x}(1-p)^{1-x} & \text{, } x= 1,0\\ 0& \text{, } x= 1,0 \end{cases}$

逻辑回归二分类任务会把正例的label设置为1，负例的label设置为0，对于上面公式就是x=0、1。

二、逻辑回归公式推导

损失函数推导

这里我们依然会用到最大似然估计思想，根据若干已知的x,y(训练集)找到一组 $\theta$ 使得x作为已知条件下y发生的概率最大。

$P(y|x;\theta )=\begin{cases} h_{\theta}(x) & \text{, } y=1 \\ 1-h_{\theta }(x) & \text{, } y=0 \end{cases}$

整合到一起(二分类就两种情况:1、0)得到逻辑回归表达式:

$P(y|x;\theta )=(h_{\theta }(x))^{y}(1-h_{\theta }(x))^{1-y}$

我们假设训练样本相互独立，那么似然函数表达式为:

$L(\theta )=\prod_{i=1}^{n}P(y^{(i)}|x^{(i)};\theta )$

$L(\theta )=\prod_{i=1}^{n}(h_{\theta }(x^{(i)}))^{y^{(i)}}(1-h_{\theta }(x^{(i)}))^{1-y^{(i)}}$

对数转换，自然底数为底：

$l(\theta )=ln L(\theta )=ln (\prod_{i=1}^{n}(h_{\theta }(x^{(i)}))^{y^{( i)}}(1-h_{\theta }(x^{(i)}))^{1-y^{(i)}})$

化简，累乘变累加：

$l(\theta )=ln L(\theta )=\sum_{i=1}^{n}(y^{(i)}ln (h_{\theta }(x^{(i)}))+(1-y^{(i)})ln (1-h_{\theta }(x^{(i)})))$

总结，得到了逻辑回归的表达式，下一步跟线性回归类似，构建似然函数，然后最大似然估计，最终推导出 $\theta$ 的迭代更新表达式。只不过这里用的不是梯度下降，而是梯度上升，因为这里是最大化似然函数。通常我们一提到损失函数，往往是求最小，这样我们就可以用梯度下降来求解。最终损失函数就是上面公式加负号的形式:

$J(\theta )=-l(\theta )=-\sum_{i=1}^{n}[y^{(i)}ln (h_{\theta }(x^{(i)}))+(1-y^{(i)})ln (1-h_{\theta }(x^{(i)}))]$

三、逻辑回归迭代公式

1、函数特性

逻辑回归参数更新规则和线性回归一模一样：

$\theta _{j}^{t+1}=\theta _{j}^{t}-\alpha \frac{\partial }{\partial _{\theta _{j}}} J(\theta )$

(α表示学习率）

逻辑回归函数：

$h_{\theta }(x)=g(\theta ^{T}x)=g(z)=\frac{1}{1+e^{-z}}$

( $z=\theta ^{T} x$ )

逻辑回归函数求导时有一个特性，这个特性将在下面的推导中用到，这个特性为：

$g{(z)}'=\frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})=g(z) (1-g(z))$

回到逻辑回归损失函数求导：

$J(\theta )=-\sum_{i=1}^{n}[y^{(i)}ln (h_{\theta }(x^{(i)}))+(1-y^{(i)})ln (1-h_{\theta }(x^{(i)}))]$

2、求导结果

$\frac{\partial }{\partial \theta _{j}} J(\theta )=\sum_{i=1}^{n}(h_{\theta }(x^{(i)})-y^{(i)}) x_{j}^{(i)}$

这里我们发现导函数的形式和多元线性回归一样。

逻辑回归参数迭代更新公式：

$\theta _{j}^{t+1}=\theta _{j}^{t}-\alpha \sum_{i=1}^{n}(h_{\theta }(x^{(i)})-y^{(i)}) x_{j}^{(i)}$

3、代码实战

（1）加载数据并拆分

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection irport train_test_split

# 1、数据加载
iris = datasets.load_iris()

# 2、数据提取与筛选
X,y = datasets.load_iris(return_X_y=True)
cond = y != 2 #过滤数据：类别为2，过滤掉
X = x[cond]
y = y[cond]

拆分训练数据和测试数据：80%为训练数据，保留20%为测试数据

# 3、数据拆分
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)

display(X_train,shape,X_test,shape)
display(y_train,shape,y_test,shape)

（2）训练数据

model = LogisticRegression()
model.fit(X_train,y_train)

y_pred = model.predict(X_test)
print('预测结果是：', y_pred)
print('真是类别是：', y_test)

proba_ = model.predict_proba(X_test)
prnt('预测概率是：\n', proba_)

I0420AY

关注

24
点赞
踩
40

收藏

觉得还不错? 一键收藏
0
评论
机器学习｜逻辑回归

逻辑回归是一个分类的算法，它基于多元线性回归，正因如此，逻辑回归这个分类算法是线性的分类器。逻辑回归中对应一条非常重要的曲线S型曲线，其对应的函数是Sigmoid函数图1 sigmoid曲线逻辑回归就是在多元线性回归基础上把结果缩放到0~1之间。越接近1越是正例越接近0越是负例，根据中间 0.5将数据分为二类。其中就是概率函数：我们知道分类器的本质就是要找到分界，所以当我们把0.5作为分类边界时，我们要找的就是，即时，的解。
复制链接

扫一扫