目录
摘要
在本周中,通过阅读文献,了解使用PINN在取代CFD求解器中存在的挫折与困难,文章使用两个案例进行说明,案例1说明了PINN的精度和性能基准,第二个案例虽没有获得理想解,但却总结除了目前遇到的问题与困难。在Fluent中,选用阶梯管的流动分析,进行几何划分和设置求解。理论学习方面,对有luent算法基本知识进行了学习。
Abstract
This week, I read the literature to understand the frustrations and difficulties of using PINN to replace CFD solvers,which using two case studies, Case 1 illustrates the accuracy and performance benchmarks of PINN, and the second case does not achieve the ideal solution, but summarizes the problems and difficulties encountered so far. In Fluent, practiced the flow analysis in the stepped pipe is selected to solve the geometric division and setting. In terms of theoretical learning, the basic knowledge of Luent algorithm was learned。
文献阅读:流体模拟中PINN的经验报告:陷阱和挫折
文献摘要
尽管pinn现在被认为是传统CFD求解器的补充而不是替代品,但它们在没有给定数据的情况下求解Navier-Stokes方程的能力仍然引起了人们的极大兴趣。本报告介绍了用PINN代替传统求解器求解Navier-Stokes方程的实验。目标是:通过该实验,让对无数据pin感兴趣得读者为可能面临的挑战做好准备。
使用了两个标准的流动问题:Re = 100的二维Taylor-Green涡旋和Re = 200的二维圆柱体流动。PINN方法解决了二维Taylor-Green涡旋问题,结果可以接受,将该流作为精度和性能基准。大约需要32个小时的训练,才能使PINN方法的精度达到16 × 16有限差分模拟的精度。另一方面,二维圆柱体流不会产生物理解。PINN方法表现得像一个稳定流求解器,没有捕捉到涡脱落现象。
PINN方法仍然是一个正在进行中的工作,特别是在没有任何给定数据的情况下解决流动问题方面。需要做更多的工作,使PINN在此类应用中的实际问题中可行。
讨论|结论
PINN方法是一种将深度学习纳入CFD应用的方法,其中求解偏微分方程起着关键作用。通用近似定理([Hor])表明,只要网络足够大,神经网络就可以高保真地对Navier-Stokes方程的解进行建模,并捕获复杂的流细节。PINN方法的思想可以追溯到[DPT],而PINN这个名字是在[RPK]中创造出来的。在应用PINN [LMMK]时,不需要人为提供数据,这使其成为传统CFD求解器的潜在替代方案。
尽管无数据PINN作为传统CFD求解器的替代方案听起来很有吸引力,但PINN更适合在数据驱动的配置下使用。由于其精度和效率较低,PINN并不意味着取代现有的CFD求解器。
PINN最有用的应用应该是那些有一些给定数据的应用,因此模型是根据数据训练的。例如:当我们有来自传统CFD求解器的实验测量或部分模拟结果(粗网格数据,有限数量的快照等)时,PINN可能有助于重建流或作为替代模型。
无数据PINN可能比传统求解器提供一些优势:
- 它是一种无网格方案,有利于流体流动与复杂几何物体相互作用的工程问题。
- 训练模型近似于控制方程的一般解,这意味着不需要针对不同的流量参数反复求解方程。例如,以边界速度线为输入参数的流动模型,经过训练后可以预测不同边界速度线下的流动。
此功能可以在工程设计优化等情况下提供帮助:运行一系列实验以进行参数扫描并找到产品的最佳值或几何形状的过程。
即使在旨在改进PINN的文献中,通常也只能看到简单CFD问题的成功案例。在这些成功案例中,关于pinn在实际和现实世界应用中的可行性的重要信息往往是缺失的。例如,很少有报告讨论所需的计算资源、训练的计算成本、收敛性质或PINN的误差分析。由于需要高阶自动微分和多目标非线性优化,PINN存在性能和可解性问题。使用自动微分来评估高阶导数增加了神经网络的计算图。多目标优化减少了微分方程、初始条件和边界条件的所有残差,使得训练难以收敛到足够小的损失值。
流体流动是敏感的非线性动力系统,其中输入的微小变化或误差可能产生非常不同的流场。因此,为了得到正确的解,PINN中的优化需要将损失最小化到非常接近于零的值,这进一步损害了方法的可解性和性能。
理论基础
NS方程
不可压缩矢量形式的Navier-Stokes方程由连续性方程和动量方程组成:


式中:U为速度场,P为标量场,都是计算域中空间坐标W和给定极限t之前的时间的函数。引力场~g也可以是空间和时间的函数,通常是一个常数。
NS方程的解需要一个初始值和一个边界值来进行求解,如下表示:
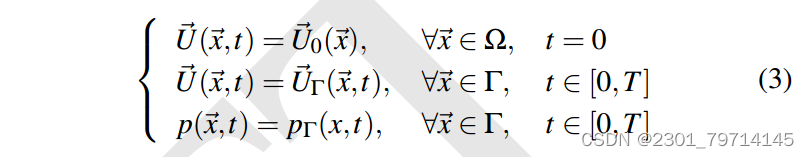
Γ即为计算域的边界。
标准PINN
使用神经网络逼近U和P,如下所示:

使用一个同时预测压力场和速度场的网络。也可以分别为它们使用不同的网络。在这项工作的后面,我们将使用gu和gp来表示来自神经网络的预测速度和压力。此时的Q表示网络的自由参数。为了理想地确定自由参数,希望方程(1)、(2)、(3)的近似解残差为零,表示如下:
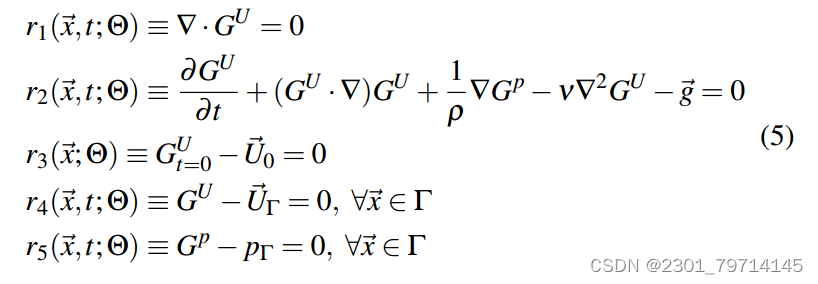
如果(5)中的残差不复杂,且参数NQ的个数足够小,我们可以通过求解由合适的NQ时空点生成的NQ非线性方程组,在数值上找到零根。然而,这种情况很少发生,因为G通常非常复杂,而NQ很大。而且,我们甚至不知道式(5)中的方程是否存在这样的零根。
而在PINN中寻找的是残差接近于0的一组数据,输入是时空坐标,输出是我们感兴趣的物理量。PINN中的损失函数或目标函数是调节目标物理量如何表现的控制方程。控制方程的使用消除了对真实答案的需要。
物理学中的大多数控制方程通常是微分方程(例如,热方程)。主要区别在于现在的PINN方法需要自动微分来评估损失。无论控制方程的形式如何,时空坐标是训练过程中唯一需要的数据。因此,在本文中,训练数据是指时空点,不涉及任何预测量的真实答案。
案例1:泰勒-格林漩涡
泰勒-格林涡旋代表了一类具有特定形式的二维、三维解析初始流动条件的流动,:V0 = L = r = 1:0, n = 0:01。这些参数对应于雷诺数Re = 100,图1显示了t = 32时的速度快照:
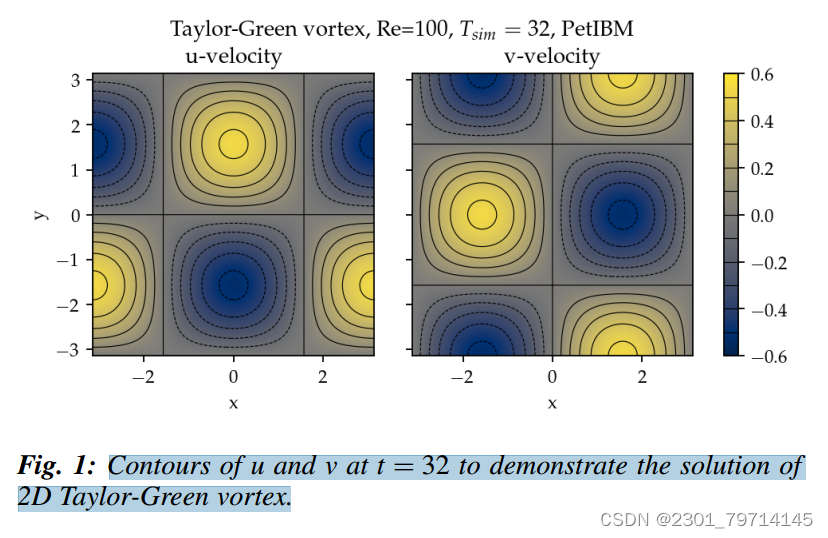
在这项工作中,使用了以下二维泰勒-格林涡,V0表示t = 0时的峰值(也是最低)速度:
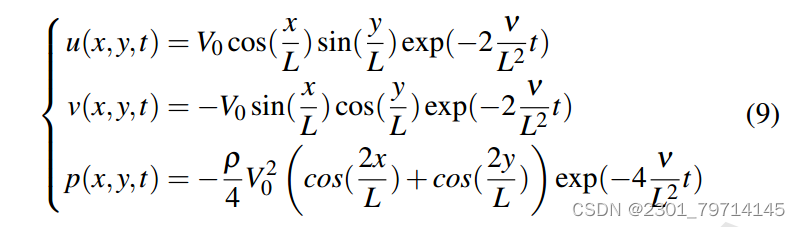
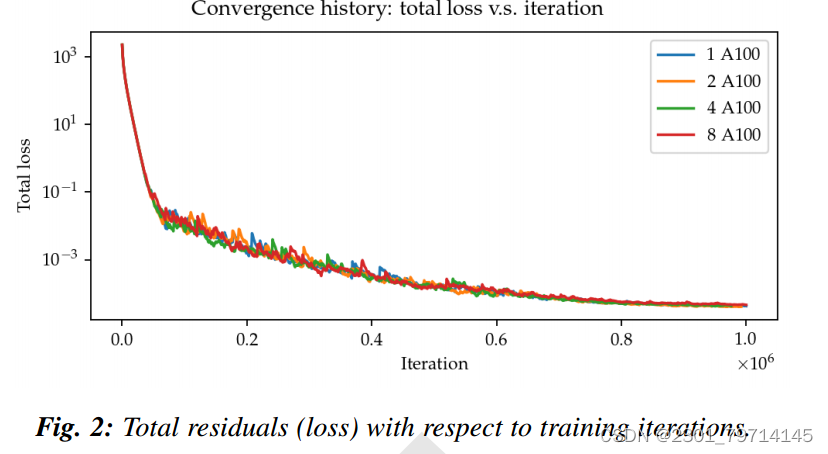
使用不同数量的gpu进行训练,以研究PINN求解器的性能。所有的案例都经过了100万次迭代的训练。请注意,并行化是在弱缩放的情况下完成的,这意味着增加GPU的数量不会减少每个GPU的工作负载。相反,增加gpu的数量会增加训练点的总数和每次迭代的数量。因此,我们的预期结果是,所有情况都需要大约相同的墙时间来完成,而使用8个gpu的残余将收敛得最快。
训练后,根据解析解在512×512笛卡尔网格的细胞中心上评估PINN求解器的预测误差(即精度)。根据这些空间分布的误差,我们计算给定t的L2误差范数:

PINN求解器使用单精度浮点数,而PetIBM使用双精度浮点数,进行了7次不同空间分辨率的PetIBM模拟:2k ×2 k, k = 4;5;:::;10。每个空间分辨率的时间步长为Δt = 0.1/2 ^k−4。图2显示了总残差的收敛历史:在弱缩放中使用更多的gpu(即更多的训练点)并没有加速收敛,这与我们的预期相反。所有的例子都以相似的速度聚集在一起。虽然没有定量的标准或理由,我们认为进一步的训练不会提高准确性。图3直观地展示了神经网络的预测结果:
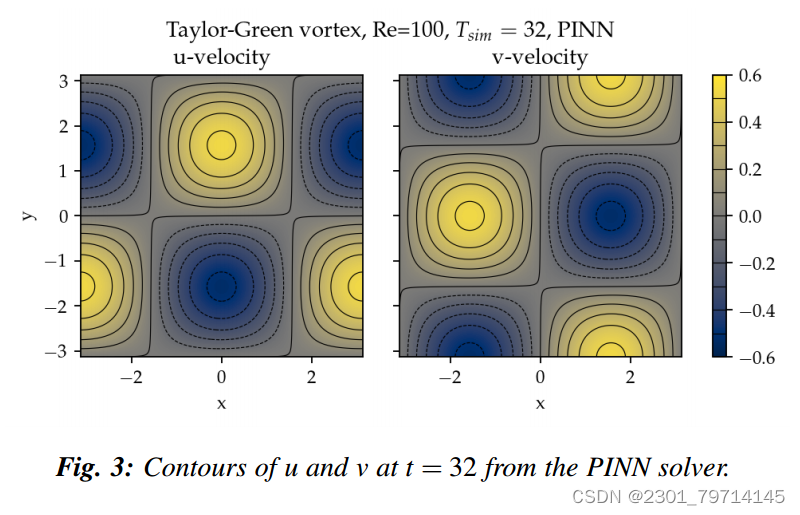
然而,如图4所示,来自PINN求解器的误差幅度远远高于来自PetIBM的误差幅度,显示了相对于t的预测误差。我们只给出了u速度的误差,因为v和p的误差是相似的,使用更多的gpu,这意味着更多的训练点,并不能提高准确率:
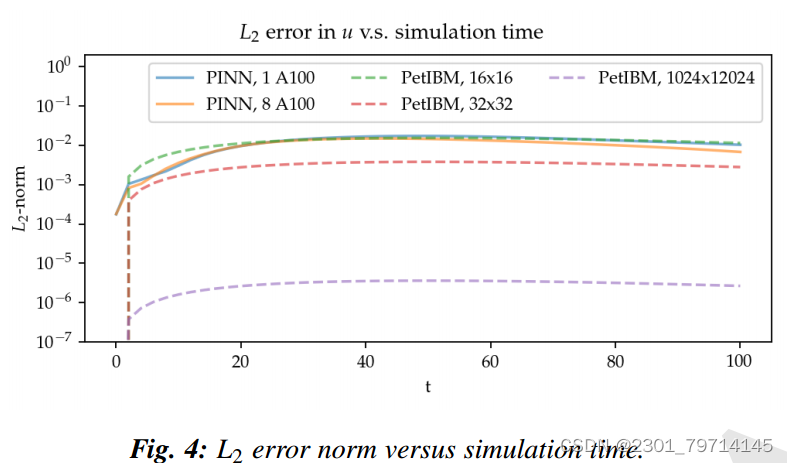
无论大小如何,对于PINN和PetIBM,误差相对于t的趋势是相似的。对于PetIBM,如图4所示的趋势表明,时间误差是有界的,该方案是稳定的。然而,这个概念不适用于PINN,因为它不使用任何时间推进方案。
我们还不清楚这对pin意味着什么。然而,它表明PINN能够将初始条件的影响传播到以后的时间,这是求解双曲型偏微分方程的关键因素。
更多的时空点并没有加快收敛速度,这可能表明单个GPU上的每次迭代点数量已经足够大了。训练点的数量主要影响残差相对于模型参数的平均梯度,然后使用基于梯度下降的优化器来更新参数。如果单个GPU上的点数量已经足够大,那么使用更多的点或更多的GPU不太可能显著改变平均梯度,导致收敛完全依赖于学习率。
案例2:雷诺数Re = 200的二维圆柱体流
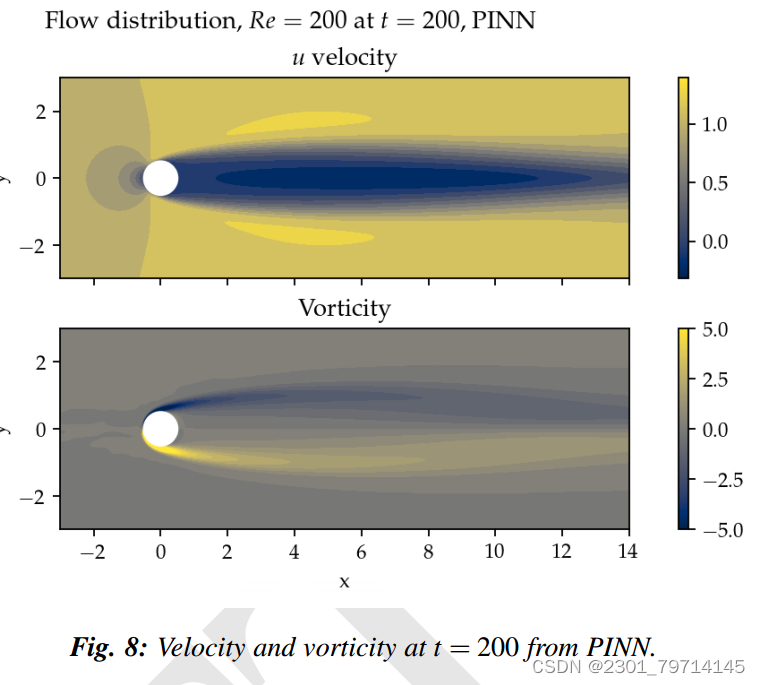
图6显示了t = 200时的速度和涡度快照:
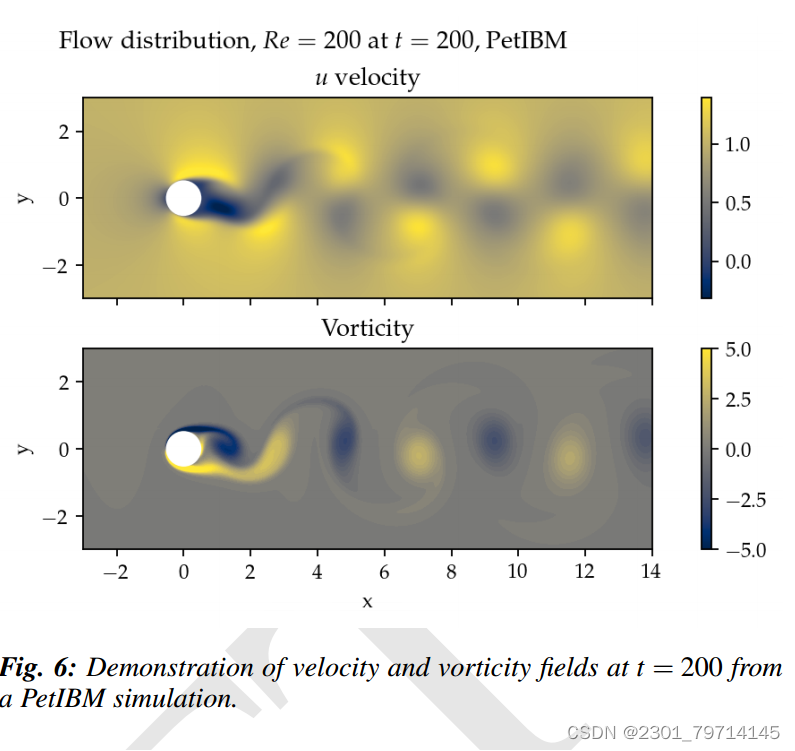
Navier-Stokes方程可以看作是一个动力系统。在某些流动条件下,流动中会出现不稳定性,并对微小的扰动作出反应,从而引起旋涡脱落。在自然界中,旋涡脱落来自于无处不在的不确定性和扰动。在CFD模拟中,计算中的小数值误差和舍入误差引起了旋涡脱落。
PINN采用两层神经网络结构,一个每层有256个神经元,另一个每层有512个神经元。所有其他网络配置都与第3节中的配置相同,除了我们允许人工干预在训练期间手动调整学习率。我们对这个案例研究的目的是成功地从PINN求解器中获得物理解,而不是进行性能和精度基准测试。
因此,将调整学习率以加速收敛或摆脱局部最小值。这一决定符合常见的机器学习实践。没有进行超参数优化。感兴趣的量是阻力系数。在系数计算中,我们同时考虑了摩擦阻力和压力阻力:

图7显示了收敛历史。历史上的起伏对应于我们对学习率的手动调整。经过64小时的训练,总损失没有收敛到一个明显的稳定值。但是,我们决定不继续训练,因为,正如后面的结果所示,即使训练收敛,结果也不正确:

图8显示了t = 200时预测的速度和涡度。图9是阻力和升力系数与模拟时间的关系。从这两张图中,我们都看不到任何使用pinn解算器的漩涡脱落的迹象:
目前遇到的问题
PINN方法缺乏定义良好的过程来控制结果。
例如,我们知道神经元和层的数量控制着模型的自由度。随着自由度的增加,神经网络模型可以近似更复杂的现象。然而:
- 当我们觉得神经网络不够复杂,无法捕捉物理现象时,我们应该采用什么策略来调整神经元和层?我们应该先增加神经元还是增加层数?减少多少?
- 当涉及到非数字时,知道使用什么以及为什么使用它更具挑战性。
- 我们应该使用什么激活函数,为什么?我们应该在所有地方使用相同的激活吗,甚至还没有考虑在这里使用不同的网络架构。
- 是否确定增加网络的复杂性是正确的途径?我们认为网络不够复杂的假设可能是错误的。
Fluent案例:阶梯管的流动分析
几何建模部分
本次建模如下图所示,从小到大的圆管管壁长度为40,50,70,100mm,管道半径从小到大为:20,30,40,50mm。通过绕x轴旋转生成模型:

网格划分部分
先通过自动划分,进行几何质量判断,若网格划分不出错,则建模封闭性足够,而后对每个圆柱体进行尺寸调整,采用分区数量命令,分为100个单位网格。都采用硬性划分,再对四个面进行面网格划分命令,分区数量采用55,网格划分结果如下图所示:

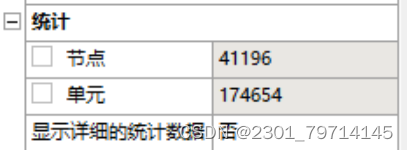
总网格数量见下图:
求解器设置
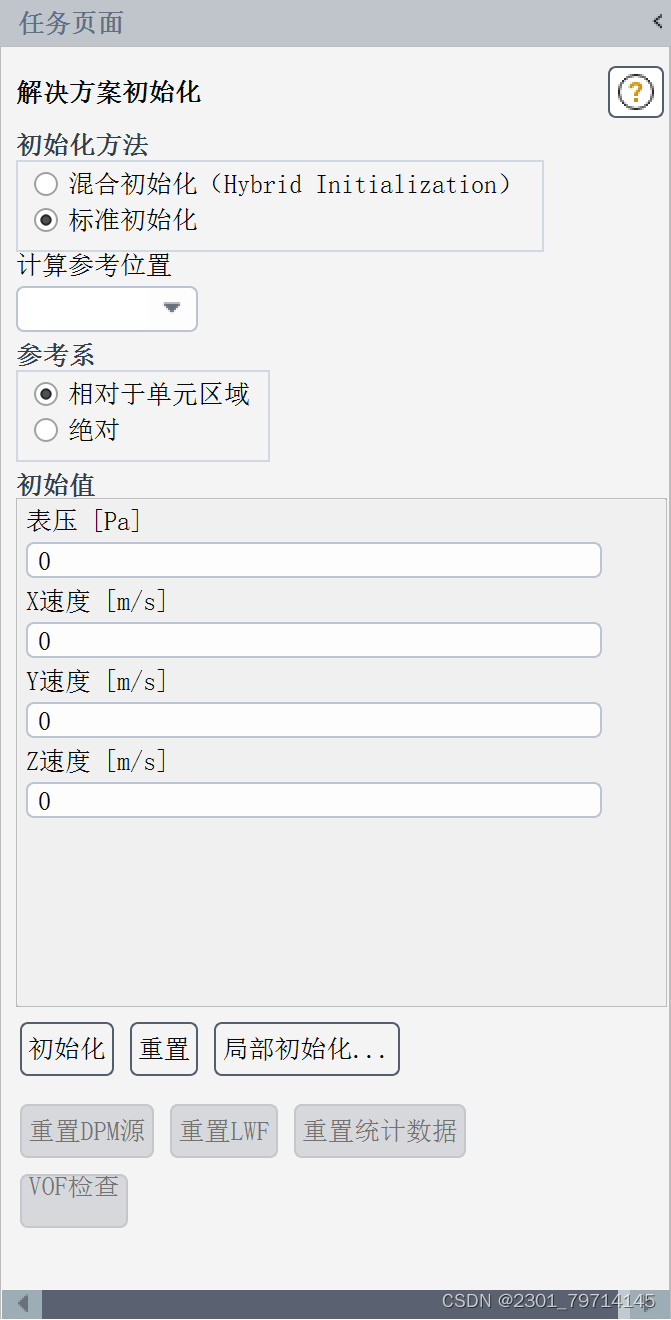
求解模式设置为层流,流体材料为水,固体材料设置为钢铁;更改流体材料为水后,设置初始条件,进口速度设置为0.001m/s,其余保持默认,采用SIMPLE方法求解,梯度采用二阶高斯区域条件来进行求解:设置残差为1e-6:对求解做初始化,计算区域为所有区域:迭代次数设置为1000次,:


结果展示
残差:

压力云图:
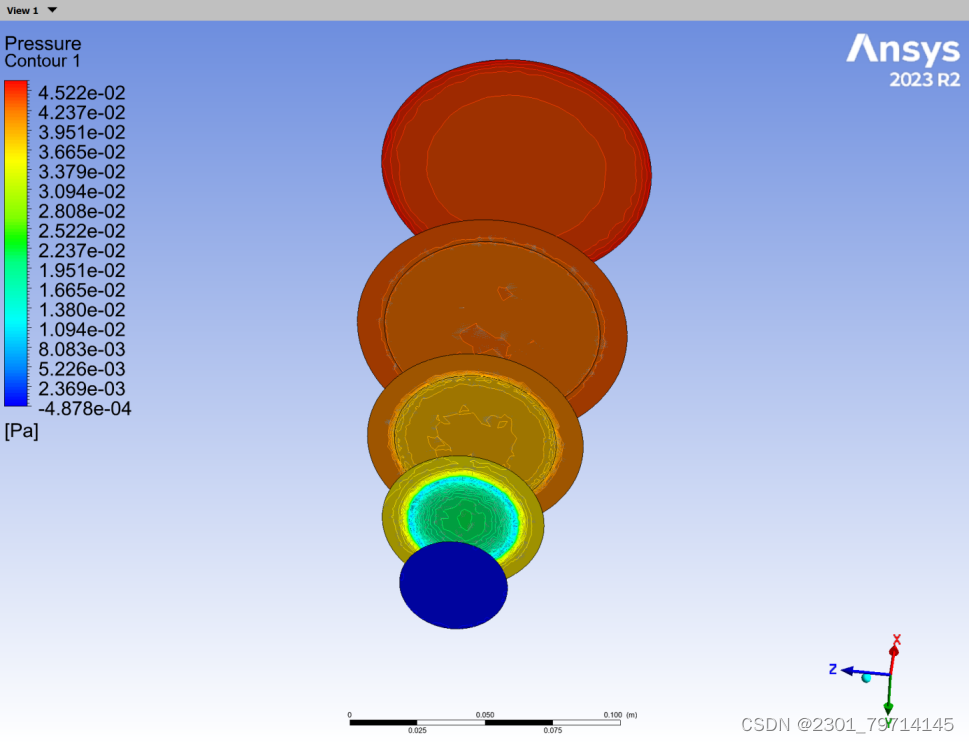
速度云图:

流线图:

理论学习部分




总结
本周通过学习Fluent相关的算法,巩固了软件的理解和使用,能更好的理解在什么情况下设置正确的边界条件和如何采取正确的求解方法来进行仿真。阅读文献时会更关注其创新点和实验方式,为了以后的写作中提供更多的灵感。





















 4598
4598











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








