笔试专题（十五）

排序子序列

题目链接

题解

1. 贪心 + 模拟
2. 1 2 3 2 2 应该是有两个排列子序列的，所以i == n-1时ret++
3. 把水平的位置和上升部分，水平位置和下降部分分为一个排列子序列

代码

#include <iostream>
using namespace std;


const int N =1e5 + 10;
int a[N];

int main()
{
    int n;
    cin >> n;
    
    for(int i = 0;i < n;i++) cin >> a[i];
    
    // 开始并不知道是上升的还是下降的,加加跳过水平的位置
    int ret = 0;// 统计最少的排序子序列
    int i = 0;
    while(i < n)
    {
        while(i + 1 < n && a[i] == a[i+1]) i++;
        if(i == n-1)
        {
            ret++;
            break;
        }
        if(a[i] > a[i+1])
        {
            while(i + 1 < n && a[i] >= a[i+1]) i++;
            ret++;
        }
        else if(a[i] < a[i+1])
        {
            while(i + 1 < n && a[i] <= a[i+1]) i++;
            ret++;
        }
        i++;// 为了让水平的部分跳过
    }

    cout << ret << '\n';

    return 0;
}

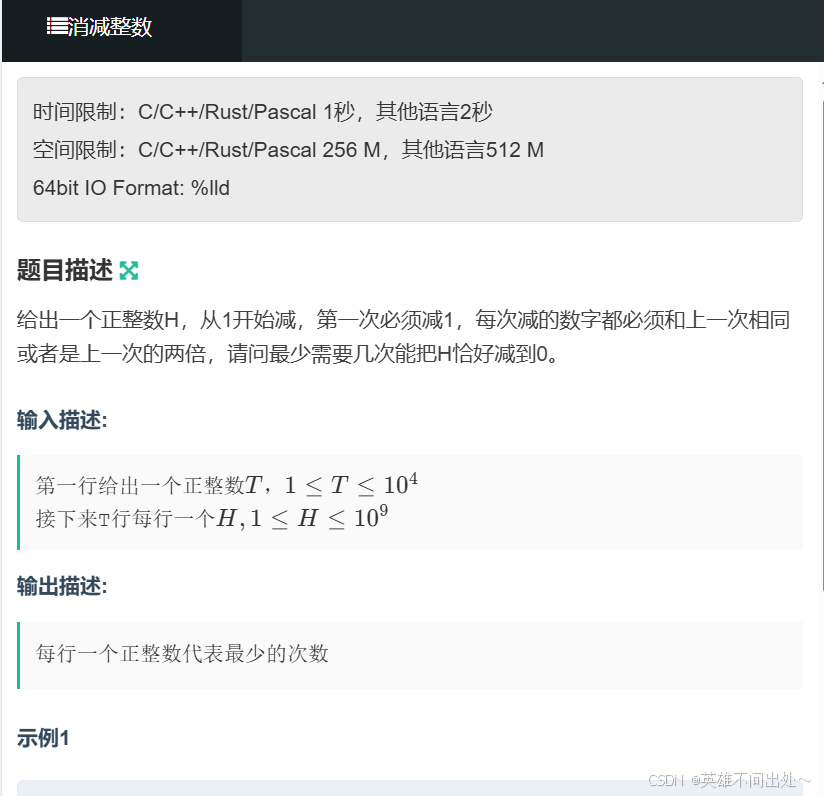
消减整数

题目链接

题解

1. 贪心 + 数学
2. 第一次必须减1，a = 1，之后的数如果是a的2倍，那么a乘2，每次ret++
3. 贪心：如果这个数模2*a == 0就一直贪心

代码

#include<iostream>

using namespace std;

int main()
{
    int t;
    cin >> t;
    while(t--)
    {
        int h;
        cin >> h;
        
        int ret = 0;
        int a = 1;
        while(h)
        {
            h -= a;
            ret++;
            if(h % (2*a) == 0)
            {
                a *= 2;
            }
        }
        cout << ret << '\n';
    }
    
    return 0;
}

最长公共子序列(二)

题目链接

题解

1. 贪心 + 二分
2. 时间复杂度：O(N*logN)
3. 动态规划的时间复杂度：O(N^2)

代码

class Solution 
{
    int dp[100010] = {0};
    int pos = 0;
public:
    int LIS(vector<int>& a) 
    {
        for(auto x : a)
        {
            if(pos == 0 || x > dp[pos])
            {
                dp[++pos] = x;
            }
            else 
            {
                // 二分
                int l = 1,r = pos;
                while(l < r)
                {
                    int mid = (l + r) / 2;
                    if(dp[mid] >= x) r = mid;
                    else l = mid + 1; 
                }
                dp[l] = x;
            }
        }    
        return pos;
    }
};