深度思考——从Transformer到大语言模型_transformer 与大语言模型-CSDN博客

本文链接：https://blog.csdn.net/2301_79726179/article/details/145330166

在文章开始之前，我想我需要先由浅入深，讲一讲，什么是transformer，什么是transformer。

transformer是为了解决什么问题而出现的。

在自然语言处理领域，生成文本的任务堪比甲方需求。想象你给了大语言模型一整篇以“凶手竟然是______”结尾的推理小说，然后问它“凶手是谁？为什么？”，那么这个模型需要做到的事情有：理解文字、记住整篇文章讲了什么事情、从文本的海洋里面大海捞针找到真正有用的线索、分辨哪些文字算名动形数量代词哪些算人物的名字等等。总而言之就是——你想要回答正确，解释优雅，那么你的模型必须完整理解文字、理解其中的关系、理解哪些字重要哪些不重要，而这是一个非常艰巨的任务。

最传统的处理方法就是rnn家族，它的想法是最简单的，就是我像人一样，看一个字我就记住一个字，然后看下一个字，我又记住一个字。在文本生成的时候，则是像正常读完了一整篇文章一样，我记住了什么，我就回答什么。

这种结构的优点在于，它非常简单，很符合直觉，但是缺点很明显，我举个例子就知道了。

如果你曾经做过阅读理解题，那么当你一个字一个字读完整个文章，一直到这个时候，由于你还没有看到题目，你就不知道你应该记住前面的什么东西。如果看到题目的时候，你才惊讶地发现：啊呀，忘记了怎么办？由于不能回头看，所以就只能错了。

后来也有很多的基于rnn的改进方案，比如GRU、LSTM等等，还有的改进出往回看的机制，上面的缺点得到缓解，生成文本的质量也得到了改善。在获得较高的推理速度的同时，另一个致命缺陷也逐渐暴露出来：并行化。

并行化是什么问题？那可能就要从GPU说起，我在这里不浪费太多笔墨，简单来说就是它有很多的核心，靠着多个核心一块干活的思想，力大砖飞堆出比CPU高得多的算力。但是如果是RNN的话，他想要处理下一个字，它就必须先要拿到上一个字输出的隐藏状态。如果是一个GPU集群，几十万甚至几百万的核心，训练这个网络，在处理第一个字的时候，最多也就一个计算操作分配一个核心，几十万个核心等着那几千个核心的计算结果，你说这合理吗？

可能有人会想到，别的核心可以处理别的句子啊，这个在模型部署是没问题的，但是训练不一样。训练要在正在训练的这句话结束之前，把他们每一步的计算张量全部保存下来，因为求解损失、反向传播的时候还是要用到。要是这个时候其它的核心再多处理几个句子，那么内存就会不够用。（其实就是增大batchsize然后爆显存）

总而言之就是，可行，但是不太好训练，没法快速达到想要的效果。

还有一种解决方案就是cnn。cnn被广泛应用于图像识别领域，卷积的操作可以看成是滑动窗口+与卷积核的相似度。它有一个特点，就是他会对每个文本的附近反复地卷积加深特征，对于局部的文本细节处理得非常到位。但是同时它也有一个致命的缺陷，那就是所谓“感受视野”。

假设卷积核的大小是3，那么每一层，他都会注意到它邻近的那两个元素，然后在下一层，借助隔壁那个元素在前一层的处理，它能够“看到”距离范围在0到2之间的元素。以此类推，假设网络一共有100层，那么它能够看到的最大距离就是100个字远。且不提最边边的信息能不能经过100层后仍然能成功流向中间，万一你的输入是101个字，那在输出的时候，他就看不到第一个字了。

总而言之，也可行，但是没法很好的进行长距离依赖的建模。

那么有没有什么网络能够既能做到并行计算，又能长距离建模呢？Transformer。

transformer其实是种在2017年提出的，全新的一种网络（attention is all you need），不同于以往的各大网络类型，它通过“注意力”机制，能够在一次传播之内，获取到远距离的信息。不像cnn靠感受视野慢慢移动，也不像rnn纯靠记忆看看前面的东西记住没记住。

下面搞张图直观看看对比：

来源：李沐-动手学深度学习v2-67-3：49

就拿上面那张图举例，想要让x1的信息与x5的信息产生关系，那么CNN要经过两个卷积层，才能在x3出找到交集，RNN则相当于要等待x1的信息流过x2、x3、x4才能与x5交流，而transformer能够直接让x1“注意到”x5，一层即可。而且重要的一点是，transformer的是直接产生信息交流的，与cnn或rnn相比，它被其它元素干扰的风险更小。

讲完作用，接下来讲原理。

self attention自注意力机制。

这个部分需要少量的线性代数基础，那就是矩阵乘法是什么东西。

假设有两个矩阵，A和B

$A=B=\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}$

那么A与B的矩阵乘法就是：A的i行于B的j列逐个元素相乘，得到的结果直接相加，放到结果C的位置（i，j）处。

比如C的（0，0）处（或者第一行第一个元素）的值就等于：

A的行：1 2 3

B的列：1 4 7

—————

$c_{(0,0)}=$ 1 + 6 + 21 = 28

如果你仔细想一想，矩阵乘法似乎对矩阵的形状有一定的要求，那就是A的行元素数量需要与B的列元素数量相等，要不然就乘加不了了。这是一个相当重要的特性，到了后面会经常用到。

接下来我们就正式开始说说，这个自注意力机制。

transformer所使用的是缩放点积注意力，英文简写叫SDPA。我从论文里面翻出来一张图，可以简单理解一下：

sdpa的计算从这张图里面，是从下往上的。它大致经过了QK先矩阵乘法、缩放、掩码、softmax最后与V进行矩阵乘法的操作。

写成数学表达式就是：

$QK=Q\cdot K^{T}$

$Score=Softmax(\frac{QK}{scale}+mask)_{dim=-1}$

$Attn=Score \cdot V$

其中，mask是可选项，scale通常选择 $\sqrt{dk}$ ，即Q或K通道数量开根号。

接下来是详细的解释，就以最常见、最简单的QKV三个张量是形状相等来举例吧。

首先我们指定，QKV的张量形状为[ batch, length, channels ]，第一个维度是批大小，这个可以暂时看作为1即可。第二个维度是序列长度，简单理解就是一句话有多长。而channels表示通道数量，也就是每一个字所包含的语义信息。

我们姑且先忽略batch维度，看作是1即可，不影响实际的计算。那么此时可以把最后两个维度看作矩阵的高和宽，分别是length与channels。此处就以长度为4，通道数为3简单举例，那么Q、K的转置可以看作一下矩阵：

$Q = \begin{bmatrix} q_{11} & q_{12} & q_{13} \\ q_{21} & q_{22} & q_{23} \\ q_{31} & q_{32} & q_{33} \\ q_{41} & q_{42} & q_{43} \\ \end{bmatrix} K^{T} = \begin{bmatrix} k_{11} & k_{21} & k_{31} & k_{41} \\ k_{12} & k_{22} & k_{32} & k_{42} \\ k_{13} & k_{23} & k_{33} & k_{43} \\ \end{bmatrix}$

注意K需要进行一个转置，让它的形状符合矩阵乘法的要求。

那么计算Q与K的矩阵乘法就是：

$QK = \begin{bmatrix} c_{11} & c_{12} & c_{13} & c_{14} \\ c_{21} & c_{22} & c_{23} & c_{24} \\ c_{31} & c_{32} & c_{33} & c_{34} \\ c_{41} & c_{42} & c_{43} & c_{44} \\ \end{bmatrix}$

其中：

$c_{11} = q_{11}k_{11} + q_{12}k_{12} + q_{13}k_{13}$

$c_{12} = q_{11}k_{21} + q_{12}k_{22} + q_{13}k_{23}$

$...$

$c_{ij} = \sum_{m=1}^{3} q_{im}k_{jm}$

计算上就是简单地将Q与K的转置矩阵相乘，我们解释一下实际发生了什么。

先看看 $c_{11}$ 为例，它表示为Q的第1个字所包含的元素，与K的第1个字所包含的元素逐个相乘，然后加和。这样就能够表示Q的第1个元素与K的第1个元素的相似度了。至于为什么，可以参考一下这个视频的9分10秒直观了解下。

那么纵观整个矩阵的组成，其实就是Q中的每一个元素与K中的每一个元素全部都求解一次“相似度”，相似度高的，它的值就大，相似度低的，它的值就会小。整个QK矩阵记载了QK中元素之间相似度的信息。其形状为 [length, length]。

这个时候你发现了，没错，这一步就能解决文章开头提出来的问题，一个序列的元素是如何做到长距离的信息交流的，这个就是关键。

接下来就是Scale这一步。这一步的思想其实很简单，就是你那么多元素乘完了又加在一起，这个数值肯定会比较离谱，所以就把它除一个 $\sqrt{dk}$ 稳定一下数值。但是如果你仔细思考一下，如果我把这个根号dk拿到前面去，比如放进k矩阵里面，直接让整个K矩阵变成原来的 $\frac{1}{\sqrt{dk}}$ ，好像数值上是相等的哇。而这个数值似乎可以在通过K矩阵前面那个线性变换学习，四舍五入来看，如果K矩阵前面是这样一个可学习的线性变换，比如pytorch里面的nn.Linear等，那么这个scale似乎没什么太大用处了。

再往下就是mask层。如果你希望前面的字能够看到后面的内容，就像做阅读题的时候，文章看一半就跳到后面看选项，那么就不需要使用mask。如果说我想然后面的字不要影响我前面的阅读，那我就直接把前面字对后面字的相似度给屏蔽掉，就是手动让它不要注意到后面的东西。这里面还有很多的门道，我们后面再说。它具体的实现其实就是给想要屏蔽掉的字，直接减去一个很大的数字，比如减去114514即可，这将在后面的softmax过程起作用。

在接下来是softmax层。先看看softmax的定义：

$X = \begin{bmatrix} x_1 & x_2 & ... & x_n \end{bmatrix}$

$expX =\begin{bmatrix} e^{x_1} & e^{x_2} & ... & e^{x_n} \end{bmatrix}$

$Softmax(X)=\frac{expX}{\sum expX}=\begin{bmatrix} \frac{e^{x1}}{e^{x1}+...+e^{xn}} &\frac{e^{x2}}{e^{x1}+...+e^{xn}} & ... & \frac{e^{xn}}{e^{x1}+...+e^{xn}} \end{bmatrix}$

用文字解释，就是首先把x转化为以e为底的指数形式。然后再求解 $e^{xi}$ 在总体中的占比。

由于 $f(x)=e^x$ 是非负的，而且较为平滑，因此可以看作是将X转化为平滑过度(soft)的概率分布。

还记得前面的mask吗？当x的值被减去了非常大的数的时候， $e^x$ 就非常接近于0了，也就是“不可能注意到它”的意思。

如果你曾经玩过大模型，那么你可能会见过一个叫tempreture的参数，其实它就是在softmax之前，对X直接相除的一个常数，温度为1的时候就是标准的softmax，而当温度更低的时候，表示模型更愿意选择数值最大的那一个，x除了一个比1小的数，相当于元素之间的差距被放大了，而指数函数求解出来的，数值较大的会被放大到更大的概率。温度更高的时候，元素之间的差距被缩小，大家被选中的概率就差不多了。不过注意的，transformer内部是标准的softmax，tempreture这个变量只影响语言模型的最后一层，跟这里是没有关系的。

在自注意力中，softmax操作被应用于最后一个维度，也就是对每一行的元素分别进行softmax，得到的结果被称为注意力分数（Score）。在pytorch的 torch.nn.MultiheadAttention 模块，它返回值的第二个元素就是这个矩阵。其形状依然为[length, length]。其中每一行表示Q的每个元素，对K的相似程度。

至于为什么是对最后一个维度进行softmax，我认为是与后续Score于V的矩阵乘法有关，我接下来详细讲解。

$Score = \begin{bmatrix} c_{11} & c_{12} & c_{13} & c_{14} \\ c_{21} & c_{22} & c_{23} & c_{24} \\ c_{31} & c_{32} & c_{33} & c_{34} \\ c_{41} & c_{42} & c_{43} & c_{44} \\ \end{bmatrix} V = \begin{bmatrix} v_{11} & v_{12} & v_{13} \\ v_{21} & v_{22} & v_{23} \\ v_{31} & v_{32} & v_{33} \\ v_{41} & v_{42} & v_{43} \\ \end{bmatrix}$

同样的，矩阵乘法得到的是[length, channels]形状的矩阵，与QKV的输入形状相同。

我们先将目光放在Score的第一行上，记得它的意思是Q的第一个元素，对于每一个K元素的相似度。假设Q的第一个元素对K的第三个元素有很高的相似度，也就是Q“注意到”了K的第三个元素，此时c13的值将会高于其它的元素。那么在矩阵乘法进行的第一行里，V对应的v31，v32，v33都会乘以一个比较大的数，连在一起就是第1个元素的注意力输出中，第三个元素的语义会占有较大的比例。

这样有什么意义呢？下面是论文给出的图例（原文图片就是躺着的，看不清可以把屏幕或者头歪90度看）：

这幅图里面，深色的线就像刚才例子中的c13一样，Q与K有很高的相似度，也就是K的第三个字会较大程度地影响Q第一个字的语义。在这副图里面，下方深色线的那两个词的语义，会较大程度影响上方那个词的语义。

最终，sdpa的输出，就是每一个元素，与其它所有元素进行比对后，根据注意力高低形成的新的，具有“需要注意到”的信息的输出。它的特点张量形状不变，可以处理任意长度的序列输入被众多人所看重，因此你可以看见把transformer到处塞的各种网络，其本质原因就是它这个特性。

多头注意力

自注意力讲解完了，那么多头注意力其实就相对好说了。这里贴两张图方便理解，一个来源于netron，另一个是论文图片：

多头注意力与前面的自注意力有什么关系呢？其实算一种改进关系。

想像下你的Q、K，如果我堆通道数量，堆叠到2048的channels，那我在进行QK的矩阵乘法的时候，我就是2048长度的向量在比较相似度。

我们知道，每一个channels应该代表一种特征，多个channels的组合可能会表示某种特性。具体一点，假如我想要找到“猫”对应的特性，那么我需要的是“毛茸茸的”、“四脚着地”、“有尾巴”的这些具体特征即可。

但是对于语言模型来说，2048个长度的通道向量还可能包含“三角形的”、“是个天体”等与“猫”毫无关联的特征。那么我在提取信息“与猫的相似度”的时候，物体是不是三角形的，算不算天体，那些特征不管相似还是不相似都与我的问题无关。但是他们之间的相关性，如果直接进行矩阵乘法的话，确实会较大程度上影响我输出的结果。

那怎么办？答案是直接拆分成多个注意力“头”，比如2048的通道，可以拆分成32*64个头。意思是拆分成32个sdpa头，每一个头只需要注意其内部64通道的相似度即可。这不仅可以减少其它的特征带来的干扰，还能在一个层之内，找到更丰富的注意力关系。

从计算量上分析发现，总的计算量甚至是保持不变的，唯一不同的是，用于存储注意力分数的矩阵从1个变成了head个。

实际操作的时候，需要注意的一点就是，拆分完通道以后，需要把拆分的头的维度与序列长度维度相交换，处理完需要交换回来。

至此，整个多头注意力机制已经整理完毕，接下来，就要进化到transformer了。

编码器与解码器

还是这样，先上图，来自论文。

左边的是编码器，右边的是解码器。意思就是左边读取语义，嵌入到右边，右边根据上下文对接下来的文本进行预测输出。我们按照输入文本的顺序来，一步一步往下推，从左侧开始。

首先是Input Embedding，就是词嵌入。我们知道计算机中的文字都是以编码的形式存在的，这一步就是把每一个文字都映射到一个高维空间里面，变成“语义向量”。可以看看这个视频的12：30

快速了解。它将离散的文本编码，转换为连续的语义向量。等价操作就是对独热（第i个值设置位1，其余为0）的输入做一个linear变换。

位置编码

PE，也就是位置编码。在这之前其实还有一步缩放就是把输入缩放一下，让它的大小与位置编码差不多，提高位置编码的影响力，不过跟scale一样，应该也是可以被放到词嵌入的变换里面的。

原本论文里面的位置编码是sin-cos位置编码，在后面我还会介绍其它的位置编码。首先看看定义：

$PE(pos,2i) = sin(\frac{pos}{10000^{\frac{2i}{d}}})$

$PE(pos,2i+1) = cos(\frac{pos}{10000^{\frac{2i}{d}}})$

其中，i是通道维度的深度，d是总嵌入通道维度深度。pos则是实际的位置。

也就是位置编码的生成，是正弦与余弦交替嵌入的（注意i的起始为0）。如果是第0或者第1个通道，这个 $10000^{\frac{2i}{d}}$ 算出来就是1，那么

$PE(pos)=sin(pos)$ 对于通道0

$PE(pos)=cos(pos)$ 对于通道1

这里就有用上一个重要的性质，那就是三角函数的周期性。此时三角函数以 $2\pi$ 为周期，所以在这个通道上，只要是间隔为大约6.28的长度，由于数值相等，所以就会被看作相似的。

再往后，随着通道逐渐加深， $10000^{\frac{2i}{d}}$ 的数值不断增大，三角函数的周期也不断变长，表示不同间隔长度，这样通过处理不同的维度就能注意到不同周期的相对关系。比如当模型看到“他”这个代词的时候，模型会向前寻找它所指代的对象。在前面可是有很多的对象的，那么需要更加注意到哪一个呢？模型经过学习，知道需要更倾向于寻找距离近的那一个，或许会将更多的注意力放在深层的位置编码上，因为深层的周期更长，可以对距离产生更精确的把控。这也为长文本的位置关系处理奠定了基础。

现在生成了sin-cos位置编码，我要怎么放到原始输入去呢？链接在一起似乎是一个合理的选择，但是模型选择了最简单的直接相加。

你可能会疑惑，直接加不会破坏语义吗？没错确实会。浅层的位置编码频率高，确实会对语义造成一定的破坏，但是反过来，如果我的词就是像“虽然……但是”这种，需要往前或往后一定距离寻找关联词的，那么这一部分还能够被学习为专门处理位置信息的语义嵌入层。而且对于深层的信息来说，它们加上的sin、cos的周期都非常长，没个几千字长度都不会发生什么变化的那种，完全可以当作位置编码不存在，直接保留更多语义。

还有一个问题，就是为什么是10000这么一个规整的数字？其实就是一个经验之谈了。研究的时候发现，100似乎太多注重于短周期，100000似乎又会影响短周期的识别效果，10000这个数字不大不小效果刚好，于是就用了。其实这个与具体任务有关，像llama的长文本版本中，用到的就是500000的96维度嵌入，能够在一定程度上增加长文本的扩展能力。

铺垫终于结束，有了最基本的语义与位置嵌入的文本信息，接下来要开始相互注意、深度思考了。

编码器的QKV从哪里来？

在前面的介绍里面，你可能会产生一个疑惑，QKV从哪里来？前面介绍的时候一直都在讲相似度高的得分高，那么理论上来说自己与自己不是最相似的吗，是什么东西把相似度与注意力关联在一起了呢？

如果你注意到多头注意力里的那一张图，你会发现SDPA模块的前面与后面都有几个Linear的层（也就是线性变换、全链接层），这个就是将输入x转化为QKV的关键所在。QKV的原名叫Query（询问）Key（键）Value（值），顾名思义，生成Q的那个Linear的目的是对序列中的每一个字，都提出一个“询问”，比如这个字是“因为”，那么这个词很可能就会对整个序列提出这样一个问题：“在我的后面，谁叫‘所以’？”，并且将自己转变成接近“所以”这个词向量相近的意思。此时，K的作用就是那个叫“所以”的字会被转化成一个答案：“我叫‘所以’”。两个“所以”自然而然地就靠相似匹配上了。此时Value的作用就出现了：“如果我匹配到了‘所以’，那这个‘所以’要怎么改变‘因为’的语义呢？”

这下我们清楚了，QKV在编码器中，都是从输入X经过线性变换得到的。那么这三个线性变换又有什么不同，导致他们的作用完全不一样呢？其实，在简单的多头注意力中，这三个线性变换没有任何结构上的不同。甚至还可以为了增加并行度，直接将三个线性层合并为一个。

那既然他都是一样的，那怎样保证比如Q学习到的是“询问”而不是其它的呢？我觉得其中绝大部分是与SDPA模型的结构是相关的。毕竟模型在不断学习中会发现，先矩阵相乘出元素间相似度的，肯定不是Q就是K，而矩阵乘法是不可互换的，那么被Softmax的、与V按矩阵乘法顺序相乘的那个，更加适合被学习为Q而不是K。所以决定它是Q，是K还是V的并不是前面的线性层，而是后面SDPA的部分。

注意到注意力输出最后面还有一个Linear（或者netron里面的Gemm，其实就是线性层、全连接层的意思），这个通常被称作out，就是把纯的注意力输出进行一个简单的后处理。曾经看过有研究说这个其实是非必要的，但是在某些形式的transformer中它没法被舍弃，这个在后面会提及。

残差链接

说到残差链接，不得不提及它的开创论文，来自Resnet网络，将整个深度学习领域带到了新的“深度”。顺带提一嘴，权重初始化的He初始化也是出自大神之手。

其实resnet的做法非常简单，下面是网络残差快的结构。（虽然这是一个图像处理的网络，但是不影响对他作用的解释）

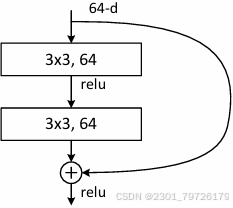
它的核心就在于，网络结构最下面的那个加号。什么意思？它的操作非常简单，就是中间放几个正常的神经网络层（此处就是卷积层）然后直接把输入加到输出上去。没错，就是简单的相加。

如果从顺着网络流向的角度看，那么中间这几层可以看作是学习到网络的“残差”，也就是输出减去输入的部分。中间的网络层学习到的是“我这个层应该把原数据改变多少”。这似乎并不能解释为什么让网络学习这个东西，就能变得更深。我们需要从另一个角度看待问题：是什么阻止了网络变得更深？

下面是没有残差链接的、18层与34层网络的对比，发现深层的网络居然比浅层的网络效果更差，这就很奇怪了，深层明明参数量更大，但是却连过拟合都做得没有18层的好，肯定是中间哪里有问题。

这里插一个笔者的题外话，我曾经拿C写过一个反向传播的简单网络，但是全部只由线性层、ReLU激活函数、Softmax输出层，MSE损失函数以及SGD优化器组成。一共5层的网络，拿CPU在非常简单的数据上训练了半天，发现训练的准确率一直保持在不到50%（四分类，完全没训练的网络也有25%正确率）。琢磨了半天才发现原因——即使迭代了上百轮，我的第一层的权重自初始化以来就没有变过。经过第一层以后，我的原始输入都被打乱了，那么我后面的网络所学习到的东西一直都是这个被打乱的映射数据，效果怎么可能会好嘛。

为什么第一层的权重完全没有被更新呢？我查看了反向传播的梯度数据发现，由于没有归一化层，从后往前到倒数第3层的时候，它的梯度就已经在10的-8次方这个量级了，加上0.01的学习率，以单精度浮点的精度来说，更新权重的时候改变的那一点点根本就可以忽略不计（其实就是完全没变）。这个现象被称作梯度消失。它的另一个极端就是梯度爆炸，也就是各大炼丹大师喜（ai）闻（hong）乐（bian）见（ye）的NaN。

出现这个现象的原因是反向传播的链式求导。假设我的网络只有三层的线性+sigmoid激活函数，然后我求解完了损失，我现在要反向传播回第一层，那么第一层对损失求解梯度就是：

$\frac{\partial L}{\partial W_1} = \delta_1 \cdot x^T = \left( (\hat{y} - y) \cdot W_3 \cdot \sigma'(z_2) \cdot W_2 \cdot \sigma'(z_1) \right) \cdot x^T$

看不懂？没关系，不需要看懂。我解释一下：这个 $\hat{y} - y$ 就是MSE损失求导得到的，损失的目的就是让预测值与真实值的差异最小化，这个减法就表示的是“现在我知道我差距在哪里了，那么我就要向自己没做好的地方移动”来更新数值。这个是网络权重更新优化表现的唯一途径。

但是看看 $\hat{y} - y$ 这一项后面跟了多少个乘法，每一个乘法对它来说都是干扰项，要是后面的数值全部都是小于1的，想象一下整整34层的网络，后面跟着上百项乘法系数，即使是0.95的100次方都到0.006去了，更别提别的不稳定因素了。

这个时候，残差链接的魔法就来了。相加操作梯度是怎么流动的呢？是直接两份相同流过去。中间夹了几层的神经网络，梯度怎么传播我全部都不关心，即使它直接梯度归零了，我在计算残差块开始处分支的梯度的时候，我也能将深层的梯度直接加过来，对于上面那个梯度来说，大概是这样的感觉：

$\frac{\partial L}{\partial W_1} = \delta_1 \cdot x^T = 0.00... +(\hat{y} - y)$ （虽然不是正确的式子，但是大概就是这个意思）

想起大神的一句话：你说想让网络学习残差，它肯定要学也能学出来，这不成问题。为什么我们设计这样的网络他就能够学的好呢？那就是因为网络的设计在一定程度上引导了它的学习方向。

回归正题，transformer的残差链接贯穿始终，每一个自注意力块、每一个前馈网络块，边上都有一条箭头往后指表示残差链接。（原文的残差链接是相加后再norm的，不同网络的实现不一样）

顺带一提，别想着去掉残差链接了，《Attention is not all you need》里面展现了去掉transformer残差链接的后果。笔者个人也作过死，搞点稍微难以学习的任务（当时是RT-DETR），只要损失一大，直接就NaN喜提炉渣网络。Transformer的结构（尤其是QK点积那里，根本就像没有数值上限一样的）本身就非常容易出现梯度问题，就不要说去掉啥残差，调大点学习率啥的了。

归一化

原文使用的是LayerNorm，层归一化。在此之前用的最多的就是BatchNorm批量归一化，直到transformer开始，layernorm才逐渐流行起来。在此之前，我们需要了解什么是归一化。

其实简单来解释，就是把输入数据变成均值为0，方差为1的分布即可。而各种不同的归一化方法之间的不同点其实只是在于执行归一化的范围不一样而已。

其公式简单可以记为：

$Norm(x)=\frac{x-\mu }{s}$

其中， $\mu$ 是x的平均值，s是标准差（方差开根号）。s的求解在bn里面是无偏估计，但是在其它归一化方法中，使用的是有偏估计。除此之外，有些大部分实现里面，在处理完归一化以后，还会对每个维度进行缩放还有加上偏置，如果在梯度没有出现问题的情况下，这对模型的训练是有好处的。

还记得前面的反向传播那一长串吗？归一化其中一个作用就是让那些后面的系数都在1的附近上下浮动，最终链式相乘出来的不会太过离谱。

直观了解下各种归一化方法的不同（图源这个也是很好的文章，后面两个不常用就先别管）：

在此处说明一下BatchNorm的Batch是什么意思。它其实就是在神经网络训练的时候，会把很多个输入样本给合并成一个张量一块送进网络里面，这样可以充分发挥GPU的并行优势。传统的BatchNorm是对所有的样本，在每个通道上的所有元素进行归一化。它的思想有一点统计的味道在里面，目的是让每一个channel的激活值，即使是在不一样的输入下，它的通道的输出均值、方差都趋近相同，让训练更加稳定。（而且有几个被cnn丹农青睐的原因就是，卷积+BN在导出的时候可以直接合并，还能节省卷积的偏置权重，另外还能对batch优化，所有样本共享一个方差均值，大量节省显存）

后面的IN、LN、GN都抛弃了Batch，其中有一部分原因就是小批量下BN的表现大打折扣，具体可以看看Group Norm这篇论文，顺带一提又是何凯明大神，前面现身Resnet的大佬。

当然，在这里其实主要还是另一个原因。那就是在批量训练的时候，每个批量的序列长度都不一样，要是按照batch方向统计的话，句子长度长的不就很容易对其它的样本造成影响（主要是实验效果非常差）。所以要求不能有跨batch的统计量。

所以，transformer选择的是上面的LN（layernorm，层归一化），理论上来说就是每一个样本的所有元素进行归一化，然后再对每个通道缩放偏置。但是在实际的实现里面则五花八门的东西都被叫做LayerNorm，有上图那种LN，也有把IN叫成LN的，还有对单独通道维度进行归一化的（这种最多，就是沿着C那条边的所有元素）。原文的应该就是上图LN的那种。

层归一化目前没有什么优化的方法，所以相比IN、BN这种有反向传播的时候算的慢，显存占用多的缺点。后来研究人员为了加速计算找到了另一种叫RMSNorm的方法，直接把计算均值这步都给贪没了，这个后面再说。

归一化放在所有的残差链接相加之后，进一步提高数值稳定性。

前馈神经网络

取这个名字的也真是人才（关键就是它还是英语直译的），这么简单一个东西取这么一个名字，绝对是在劝退。就是下面这张图展示的东西：

由于我用的是SiLU激活函数，所以中间看上去有个岔路，其实是没有的。pytorch代码就下面这个，然后残差链接：

nn.Sequential(
    nn.Linear(channels, channels*2),
    nn.SiLU(),
    nn.Linear(channels*2, channels)
)

本质上就是一个线性层将通道数扩增到原来的n倍，激活函数带来非线性，然后再一个线性层转化回原来的通道数。最后加上残差链接归一化，就是整一个transformer层的输出了。

有研究说，transformer对知识的存储都存放在这里，这里也是占据整个网络绝大多数计算量与参数量的地方（如果序列没有特别长的话），论文我是找不到了。

图像领域把这种叫做倒置瓶颈结构，就是中间宽、两头窄（从通道维数上看），在图像领域有研究说如果是中间窄两头宽的瓶颈结构能够显著减少参数量，还能加速推理，同时效果不减，不知道nlp领域适不适用。

堆叠编码器

基本的简单架构已经讲述完了，现在我们需要做的就是把他们拼接在一起，堆叠编码器。

嵌入层的输出是X，X经过位置编码后，就送入编码器里面。首先经过线性变换得到QKV送入多头注意力块里面，然后输出的结果再次经过线性变换（Out）得到多头注意力的残差，残差与输入X相加并使用层归一化，得到自注意力的输出，依旧记为X。X继续经过转置的瓶颈层缩放，再与自己的输入，也就是自注意力的输出X相加，输出结果依旧记为X。

堆叠的时候，输出的X直接就进入下一个编码器里面，不需要再进行位置编码。整个编码器部分都是直接串行链接，简单的结构就有很高的效果。

可能会有疑问，分明一层多头注意力就能注意到全文，为什么还需要堆叠呢？其实就与人的思考一样，三思而后行，这样得到的结果才更准确，更好。深度学习就应该有深度思考的样子，在此处堆叠就是在增加网络的深度。

编码器中，每一个文本都能够看到上下文，没有使用掩码。如果跟现实对应起来的话，就像写作文一样，你可以在读作文题目的时候上上下下地、跳跃地看题目，将看完整个作文题目经过思考后的结果存储起来，这就是编码器的输出。

交叉注意力

在介绍解码器之前，我们看向中间的两个多头注意力层，发现加在中间这一层长得似乎与前面的不一样。它的QKV似乎来源并不单一，那它的QKV从哪里来？

在此之前还需要搞清楚的问题是解码器是干什么的。解码器要做的就是输出文本，那么在输出这个字之前，需要知道两个信息：一个是来自于编码器的，生成文本之前的预处理信息，另一个是来自已经处理生成的文字。如果使用作文来举例的话，就是写下一个字之前需要考虑的信息有读完作文题得到的思考，以及已经写过了什么。在解码器里面，这两个内容分别交给交叉注意力与带掩码的自注意力来解决。

带掩码的自注意力就是输入带掩码，这个没什么好说的，现在主要说说交叉注意力，也就是解码器夹在中间的那个多头注意力层。

交叉注意力的模型结构就是多头注意力，这一点没有一点改变，它的不同之处就在于，它的Q与KV来源于不同的渠道。从逻辑来看，这一层的作用就是现在即将生成的文字要对编码器的结果进行提问，并从编码器处得到答案。理想情况下，编码器的输出已经包含了模型在“阅读文本”时的所有思考，在输出下一个字的时候，只需要让这个字不停地向编码器思考的结果里面询问即可得到想要的答案。因此，Q是来源于解码器的掩码自注意力输出，而K和V均来源于编码器的输出。

把信息溯源，那么Q应该来源于解码器输入，也就是已经生成的文本，而KV的来源，则是生成前所阅读的文本。这个时候，你可能有一个疑惑，万一已经生成的文本与阅读的文本不一样长？那还能接着运行吗？答案是可以。

回过头来，看看矩阵乘法的限制，如果需要A与B矩阵相乘，其实只需要满足A每一行的元素数量，与B每一列的元素数量相等即可。也就是说，Q与K的转置相乘，其实只需要Q与K的通道数相同即可，所以QK即使长度不一样，矩阵乘法也依旧可以进行。此时输出的注意力分数也不再是文本注意自己，而是从别的序列（也就是编码器的注意力输出）里面寻找自己需要的答案。这种跨序列的注意力机制，就被叫做交叉注意力。

接着向下推，QK乘出来最后得到的注意力分数，它的形状是[ lengthQ, lengthK ]，而V来源于编码器，它的形状是[ lengthV ( = lengthK ), channelsV ]，此时又满足的矩阵乘法的条件，因此计算可以进行，机制并没有发生改变。其输出形状是 [ lengthQ, channelsV ]

在有的实现里面，编码器与解码器的通道数量不一样，这个时候，多头注意力中的Out线性变换就起作用了。序列是可变的，但是通道维度是不变的，O的线性变换只需要把 channelsV重投影到 channelsQ即可。这样，对于交叉注意力块的Q输入来说，又是一个输入形状与输出形状相同的模块，省去很多烦恼。

堆叠解码器

解码器的结构相对复杂，所以需要一步一步来。

首先搞清楚，解码器的任务是生成下一个字，那么此处就有一个小技巧。假设我的解码器正在生成一句话：“到此一游”。现在已经生成到“到此一”三个字，我需要的就是预测下一个字，那我可以给这个长度为3的序列直接拼上第四个字，变成 “到此一__”，表示我多占了一个位置进入解码器。经过解码器的各种注意力各种操作，最终会吸收完整个上下文中所有所需要的浅层深层语义，逐渐向“游”这个字的词嵌入输出靠拢。

当然如果你愿意的话，也可以一次性输出两个词。我联想到NV最近出的那个DLSS4，估计底层原理大概就是用这个技巧，在这里多放了三个预留的位置，一次性往后预测三帧。

回归正题，解码器怎么堆叠。首先就是输出的文本嵌入经过位置编码嵌入后，记作Y，直接送入第一个带掩码的自注意力层，通俗点解释就是在写下一个字的时候是看不到自己未来要写什么字的，所以需要一个掩码来保证“因果”正确（笔者觉得这就是在扯淡，胸有成竹的典故就是画竹子之前就想到画出来应该长什么样了，这其实算数学上以及优化的原因，后面再说）。在这里，即将预测的字将会注意到整个输出序列的所有内容，得到所有注意力输出。

接下来就是交叉注意力层，在此处，所有的文本都会与编码器的输出X进行询问，获取信息交互。最后就是一个前馈神经网络，其结构与编码器的完全一样（权重不一样哦）。中间这三个块都使用残差链接与归一化连起来。整个解码器输出依然记为Y。

堆叠的时候，依旧是以Y、X为输入，将输出继续作为下一个解码器的输入Y，而编码器的输出X在这一步不会发生任何改变。

到了最后，位于解码器序列末尾的字符吸收了非常丰富的语义，在经过一层嵌入转词汇（其实就是channels到词数量的线性层）+softmax后，就可以得到下一个词的概率分布了。最后只需要根据这个概率分布按照概率随机生成下一个字即可。比如“到此一__”，经过处理后，概率显示“游”这个字就会有很大的概率被选中，那么输出的下一个字就基本可以确定是“游”了。

自此，整个transformer的架构已经介绍完毕。

transformer的发展

终于轮到正题了，前面都是在介绍2017年最原始的transformer，而2017年距离笔者写道这里时已经有8年了。接下来我将从各个方面介绍，transformer是如何一步步走向现代的。

图像领域的广泛使用

自从transformer问世以来，其良好的性质——全局视野+输入与输出形状相同，使得它既能够带来一定的性能提升的同时，还基本可以想塞哪里就塞哪里。因此涌现出来很多transformer-based或者cnn+transformer的网络。比如ViT、Swin、CoAtNet，甚至连注重轻量化的Mobilenet v4、YOLO11都开始使用这个曾经被视为“力大砖飞”的结构。

在ViT中，图片被简单地拆分为n个图像块，展平后进行一次线性变换处理形状，加了个位置编码就直接送入了堆叠的transformer编码器里面，完全没有经过任何的卷积层。这样简单粗暴的处理，却直接在图像分类的各个计算量尺度上打赢了cnn的老牌质检员resnst。而将resnet作为骨干，后面套上vit的混合网络直接打赢当时SOTA的cnn模型（论文自己说的哈，打的EfficentNet-L2，看着就是两个巨型打榜专用模型）。这足以看出Transformer在图像领域或许具有得天独厚的长距离依赖逻辑的优势。

不过我觉得ViT这个研究最大的作用就是，它告诉大家视觉领域要用transformer的话，最好要带上位置编码。原本大家以为带不带位置编码都差不了多少，有的还认为加上位置编码会破坏网络的某些性质（不过现在也有很多网络不加位置编码的）。

后来大家发现（其实很明显），ViT的这个做法处理不了很精细的东西，因为它是把非常大一块的区域放进去进行处理的，而且万一比如有一个物体，正好被分割到左边有一半、右边有一半，那无论从哪个方面看都是会影响效果的。也就是说，图像分辨率一高，他就会丢失很多的细节。

后来就有了一个叫Swin Transformer的网络出现了。他将Transformer的作用区域限制在小的范围里面进行处理，既保证了高分辨率像素不会丢失，也保证了计算量不会由于展平长宽的平方复杂度而变得太过离谱，它靠改变作用域来实现不同窗口之间的信息交互。（论文的后半部分怎么移动怎么掩码的，其实只是为了计算加速，如果想看的话可以留意一下）

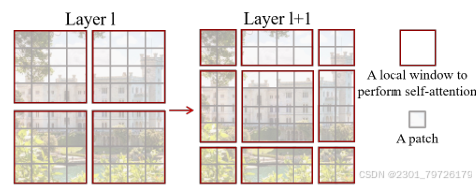
顺带提两句，convnext网络就是受到swin的启发改出来的，swin v2提到的余弦注意力我会在后面介绍。

视觉领域有没有什么对transformer比较独到的修改呢？有的。比如在ViT中的位置编码，就是1维的sin-cos位置编码或者可学习位置编码。后来有人发现，其实还有一种方法可以引入位置信息而且效果还挺好，这就是卷积位置编码。

卷积位置编码的原理其实挺随意的，就是卷积核的感受视野能够让这个元素知道它相对于上下左右的元素推断自己大致在什么地方，相当于是一个相对位置编码。

下面是YOLO11的相对位置编码实现（拿出QKV中的V的张量，卷积后直接加到注意力输出上，说实话有点迷惑，但是可行）以及美团的CPVT的卷积位置编码（魔改于ViT）。

还有另一个值得注意的研究，在CoAtNet里面，提到了浅层使用CNN，深层使用Transformer的做法，笔者认为其中最有价值的是它对模型的效果以及泛化能力的研究。此处表明，虽然transformer具有相当强大的模型能力（比如训练的loss下降的很快，能记住很多东西），但是它的泛化能力（就是在没见过的新数据上的表现）就没有纯的CNN那么好。

激活函数

生物里，神经冲动是一个类似这样的过程（图源：百度百科）：

输入电信号如果不是很强，在图中蓝色线以下的话，那么这个神经元就基本不会做出什么反应，走的就是底下那个黄色的线作为输出。但是如果输入的电信号一旦超过了蓝色这个阈值，那么输出信号将会非常大，就是图中橙色线的样子，此时说，这个神经元被激活了。（其实我觉得KNN才更像这种）

在神经网络里面也是一样，但是我们把这个叫做激活函数。函数的输入如果不大的话，那么输出就不大，但是一旦输入达到了一定的阈值，输出就会被“激活”返回一个较大的值。很老的激活函数基本上都是基于这个思想设计出来的。比如sigmoid与tanh（图源：geogerbra）

$sigmoid(x)=\frac{1}{1+e^{-x}} \\ tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$

顺带一提，这两个函数的导数特别好求。

其实在数学上，激活函数还有一个作用就是带来非线性。我举个例子看看非线性的作用：

经过计算，得到：

$Out=(In\times w1\times w4) + (In\times w2\times w5)+(In\times w3\times w6) \\ Out=In \times (w1\times w4+w2\times w5+w3\times w6)\\ Out=In\times w$

竟然发现，原本的6个权重，经过多项式化简发现，实际上其实等效于1个权重。但是如果在中间这三个圈内引入了一个非线性的激活函数，那么他就化简不了了，6个权重也就具有了6个权重的效果。

后来大家发现tanh与sigmoid这两个激活函数好像不太行啊，万一我的输入落在离0稍微远一点的地方，求完导数直接就归零了，总之就是效果不太行。后来就有了ReLU，也就是论文中使用的激活函数。它非常简单，就是把小于0的部分置为0即可，但是效果很好，直到今天依然可以说是经过最广泛验证的函数。

再往后出现了SiLU（swish）、GeLU，他们都可以被看作是ReLU的一种平滑过渡，但是它的函数形态有一个很大的特点就是在输入为负数的区域有一个小的下凹，有什么作用笔者不清楚，只知道实验结果很好。

$SiLU=x\cdot sigmoid(x)\\ GeLU=x\cdot \phi (x)=x\cdot 0.5\cdot (erf(x)+1)$

根据笔者的亲身体验，一个好的激活函数可以达到节省参数量的作用，还能帮助网络走得更深。在transformer的著名Encoder-only（仅包含编码器的模型）网络Bert里，就是把ReLU改成了GeLU。

在函数曲线上，似乎已经卷到了头，那么接下来就是带参数的激活函数，是时候见证下门控的威力了。门控的概念其实在GRU、LSTM里面都有提及，在《Language Modeling with Gated Convolutional Networks》中也是靠着门控机制，在没有transformer的时候达到了相当好的效果。它的思想本质上就是构造一个小的线性变换，然后决定这个元素我应当“开门相迎”（保持激活值）还是“拒之门外”（激活值归零）。下面是GLU的一个图示：

首先，输入经过两个缩放的线性层分别获得两个通道数相同的隐藏层张量，选择其中一个作为门控，将它的输出使用sigmoid激活函数规范到0到1之间，然后再与另一个张量逐元素点乘，得到门控输出，最后再使用一个缩放的线性层将结果映射回去。在此处，整个GLU函数不仅仅被用于替代Transformer前馈神经网络中的激活函数，它直接替换整个前馈神经网络。

如果你注意到了SiLU的函数表达式就会发现，其实SiLU、ReLU这种激活函数就是一个类似此处GLU的结构，只不过它没有分为两个线性层，而是一个线性层的输出自己对自己进行门控，比如ReLU就是大于0就“开门”，小于0就“关门”的GLU。因此这种函数也被称为自门控激活函数。

再接下来，我们回到Swish激活函数那片论文，它里面给出了一个很有意思的表格：

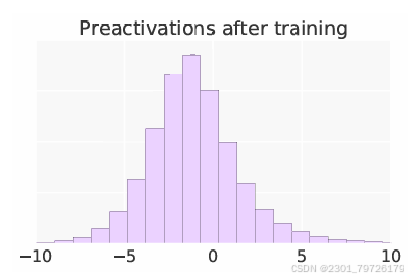
这个图说明了，在数据流向SiLU激活函数前，数据的分布情况。稍微计算下就发现，其实大部分激活值都落在0到1之间（大于1也没关系，就当是放大了），那既然SiLU声称可以直接替换大多数激活函数，那我拿来替换GLU的Sigmoid是不是很合理？

于是，替换完一测，发现真的，效果确实好啊。来源：《GLU Variants Improve Transformer》

至此，我们找出了各种激活函数对应的门控激活函数，比如GeLU的就是GEGLU，SiLU的就是SwiGLU，而这些激活函数正是大多数大语言模型正在使用的激活函数（或者说，他们的FFN前馈神经网络层）。

另外在图像处理领域，你要是想把激活函数换成SwiGLU，那笔者还是劝你三思。由于笔者的任务比较难以学习（能把rt-detr干到nan），对逐个像素操作的层来说可能学不到空间信息他就不学了。后果的话大概就是这样：

笔者个人的话接受了ResNet的思想，从反向传播的角度解决退化的问题。一个是先使用FReLU保证这个模型能够学到空间信息，让其中非门控的路径至少不会稀疏。然后在转置瓶颈处除了相乘以外，还添加了一个相加的操作。最后在相加的路径上添加一个bn，来起到一个缩放的作用。从图上来看大概就是这个样子：

在反向传播的时候，由于FReLU包含一个空间3*3的卷积，所以网络会倾向于学习这个层。而中间的这些相加的操作也可以强制让FReLU路径相关联的权重能够传播到梯度，所以至少这个网络是没有退化问题的，甚至比Linear-SiLU-Linear的结构权重更加稠密。

不过上面这个网络只是笔者的实验得到的结论，没有经过广泛验证的，不要轻易使用吧，说不定还比不过relu呢。

归一化

什么？归一化还能被玩出什么花来的吗？没错。在前文讲解编码器与解码器的时候，我埋下了一个坑，就是现在的大模型为了节省归一化的计算，把计算平均值这一步都给贪没了。

如果你看过大模型的结构，那么你会发现，现代的大多数大模型，使用的都是一个叫RMSNorm的东西。我这里直接就粘上llama3的源码实现：

class RMSNorm(torch.nn.Module):
    def __init__(self, dim: int, eps: float = 1e-6):
        super().__init__()
        self.eps = eps
        self.weight = nn.Parameter(torch.ones(dim))

    def _norm(self, x):
        return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)

    def forward(self, x):
        output = self._norm(x.float()).type_as(x)
        return output * self.weight

公式是：

$\text{RMS}(\mathbf{x}) = \sqrt{\frac{1}{n} \sum_{i=1}^n x_i^2}$

$\hat{x}_i = \frac{x_i}{\text{RMS}(\mathbf{x})}$

$y_i = \gamma_i \hat{x}_i + \beta_i$

其中 $\beta_i$ 一般是不加的。

RMS分别表示Root Mean Square，就是根号、均值、平方。看着上面的公式来说，就是求解全体元素的平方，然后求解平方均值，然后开根号就叫RMS。最后让输入直接除以RMS，然后在乘一个gamma调整以下通道权重即可。

另外，注意到RMSNorm其实是对最后一个维度求的均值，也就是说其实它操作的元素是一个词的全部通道元素，而不是一个样本中的所有元素。是与前面图里面那个layernorm不一样的（但是它其实也被叫做layernorm）。

下面的来自于论文：

图片里面那个pRMSNorm其实是更加极端的优化版本了，它求解RMS的方法是只取其中的几个维度计算（有点抽样调查的感觉了）但是transformer是有位置编码存在的，浅层的位置信息居多，不能拿来代表深层的语义信息，而且这也没快多少。

不过话说回来，如果你仔细看的话可以发现，RMSNorm与L2Norm其实就差了一个 $\sqrt n$ 。L2Norm的公式如下：

$\|\mathbf{x}\|_2 = \sqrt{\sum_{i=1}^n x_i^2}$

$\hat{x}_i = \frac{x_i}{\|\mathbf{x}\|_2}$

这就相当奇怪了，理论上来说，这个根号n是一个常数，只要RMSNorm的后面紧跟着线性变换（在pre-norm模型里面确实是这样的），那么这个常数是可以被后面的权重合并的，甚至说可以直接与RMSNorm内的gamma合并。但是论文的实验结果却表示，L2Norm的表现相当糟糕，这就很难解释了。论文说他们凭经验任务这个根号n是能让得到的值更加稳健的，反正笔者是觉得他在搪塞。笔者认为（仅个人观点，大概率是错误的）直接在RMSNorm处注册一个向后钩子，让更新gamma的梯度减小到原来的根号n就差不多了。

还有一个问题是究竟是pre-norm还是post-norm。post-norm就是原文提到的后归一化。而pre-norm则是把归一化提前到每个模块之前，残差链接的分支之后那里。

有过一些实验研究，说transformer到底是pre-norm好，还是post-norm好。目前来看总结出一些定性的结论（更像是经验吧）。就是pre-norm训练快，post-norm效果好。至于为什么几乎所有的大模型都使用所谓效果没那么好的pre-norm呢？我想这篇可能会有一定的帮助：《为什么大模型结构设计中往往使用postNorm而不用preNorm》https://blog.csdn.net/stephen147/article/details/140063465https://blog.csdn.net/stephen147/article/details/140063465https://blog.csdn.net/stephen147/article/details/140063465https://blog.csdn.net/stephen147/article/details/140063465https://blog.csdn.net/stephen147/article/details/140063465

个人的看法是，post-norm一个是需要warmup（学习率从0开始逐步上升，然后再逐步下降），要不然分分钟给你来个NaN，直接让投入的经费时间全部打水漂，与其赌warmup的轮数，不如直接选择pre-norm解决一切。还有一个可能就是现在的大模型还远远没达到其容量的上限，只要愿意继续往下炼，它还能更好，以至于像文章所说的那样：

《On Layer Normalization in the Transformer Architecture》这篇论文中显示Pre Norm要好于Post Norm。

但其实这篇文章比较的是在完全相同的训练设置下Pre Norm的效果要优于Post Norm，这只能显示出Pre Norm更容易训练。通常Post Norm要达到自己的最优效果，不能用跟Pre Norm一样的训练配置。
————————————————

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

原文链接：https://blog.csdn.net/stephen147/article/details/140063465

对了，为什么pre-norm训练快，笔者认为应该是跟残差链接有关系。post-norm的残差链接后面还需要跟着一个归一化层，而pre-norm的每个残差链接之间都是直接相连的。

位置编码

在transformer后续的语言模型中，大家发现你原文这个sin-cos位置编码好像有不少道理，但是不够用啊。所以在这个架构刚刚出现的时候，可学习的位置编码就非常热门，但是固定的位置编码依然在蓬勃发展。

首先，我们先来回顾位置编码是要解决什么样的问题。位置编码最主要解决的是比方说字的顺序，词的顺序，句子，段落等等的顺序，它需要保证“奶牛”能够被识别为一种动物而不是一种液体。那么我们回到自注意力机制去，究竟是那个模块在管理这个顺序，或者说有造成真个问题的可能呢？其实就是QK相乘的那一块。那我问你，这个次序关系与V有关系吗？答案是没有，它做不到这个。

那么如果我把这个最开始那个位置嵌入换个地方，换到第一层的QK嵌入，那不就足够了吗？这样输入可以包含更多的语义信息而非位置信息，性能怎么提升我倒是没找到什么实验结果，但是把位置嵌入放在最前面已经没有大模型在使用了。现在，位置嵌入被放在了生成QK那个线性变换的前面，也有少量的做法是把这个放在线性变换后面的。

不知道是因为这种位置嵌入的方式表达能力不足，还是外推性有一定的问题，亦或者是忽然发现把位置编码放在QK处可以更加大胆地进行更多嵌入，总之就是大家觉着位置编码只放一层不够，所以每一层都有这样的嵌入。（不够这种处理在纯编码器架构的居多，解码器的倒是很多都是可学习位置编码，当然还有不少其它的位置编码方案，取决于具体任务）

这些编码其实都有一个问题。那就是在训练的时候，最长的训练文本长度一般是4096的长度，模型只能靠这4096长度内的位置编码信息，管中窥豹地学习位置编码的含义。这就对位置编码的外推能力产生了极大的挑战。早期大语言模型中并没有很适合外推的位置编码，他们上下文长度一般不超过4096的原因，有一部分就是因为这个，在大于4096长度的时候，模型的性能会直线下降。（当然还有一部分原因是，当时还没有flash attention这种优化，二次复杂度在长序列下开销非常大）（图源，虽然不是sin-cos位置编码，但是大概是这个意思，sin-cos的效果比最下面那条还要差）

前面的只是铺垫，接下来的就是大神了。现在全部大模型的位置编码，除了少数使用的是ALiBi，其它都是叫旋转位置编码（RoPE）的编码方式，足以证明其良好的位置表达能力。

RoPE是怎么实现的呢？论文里面贴的是这张图，虽然瞪眼看不是很容易看明白，但是大概的思想就是这样一个思想。

正如sin-cos位置编码一样，每两个通道合作一组，使用的是同一个频率，比如sincos的做法是偶数项为sin（因为从0开始），奇数项为cos。

RoPE不这样处理。它把这两个数看作平面上的一个点，点的横坐标为偶数项的数值，纵坐标就是奇数项的数值，就像上面那张图x1、x2对应的向量。然后，使用sin-cos位置编码同款的频率计算公式（也就是通道维度上越深，频率越低，旋转得越慢，周期越长），得到当前这个点所对应的旋转角速度。接着，按照这个旋转角速度乘以位置（想象一下转动，角速度x时间=旋转角度）即可得到当前位置的旋转角度。最后，将最开始那个点绕中心旋转这个角度，再把此时点的位置坐标映射回QK处即可。

对的，就是两两看作一个点，然后按周期旋转，再映射回去，就是这么简单。我下面来解释一下，为什么它会那么有效。

首先，经过初始化以后，生成的点都正好落在大概在距离原点为1的这个圆上（这种初始化方法好像被RoPE的作者提到过，找不到文章了）。但是我们先假设一个比较极端的初始化条件，那就是全部初始化到（1，0）这个点上。

接着就是执行旋转操作，浅层转的角度大，周期短，深层转的角度小，周期长。那么在QK进行相似度对比的时候，单独在各自的维度上进行对比如果这两个向量方向都差不多的话，那么对应的那两个维度将会求解出更高的相似度，也就是“Q会注意到大概θ（周期）距离处的向量”，也就是两者之间的相对位置就被编码了。旋转的图示如下（其中vec1，vec2为Q或者K分别经过位置编码生成的）：

这个时候，要是光注意到这个固定的周期肯定不行，首先想要做的是，我那么多个周期，有的周期是我不想要的怎么办？比如好不容易被注意到的θ周期的向量，结果被2θ周期维度上那两个相反的向量给影响，两个周期的总相似度又归零了，那怎么办？那么模型在学习位置信息的时候，会觉得这2θ周期的并不是我所需要注意的周期，就会把对应周期维度上的向量长度减小，那么这个维度对应的向量就不会对QK的相似度有太多影响了。

如果我不想只能注意固定周期怎么办？那还可以让模型学习点的位置，让QK生成的对应向量有一个初始夹角，这样行走一定的位置之后就可以重叠了。

经过网络的学习，模型可以学习到更加复杂的位置关系，模型的整体效果也更好（模型不需要去猜测自己没学过的绝对位置应该长什么样，而是相对位置即可。同时，近距离的细节也被保留）

接下来贴一下原文里面的公式，也就是使用矩阵乘法的形式来描述这个变换：

分解为：

RoPE位置编码一举改变了可学习位置编码独占大模型江山的局面，现在则是RoPE的天下了。

后来llama2的研究者在研究长序列的模型的时候发现RoPE外推能力也没有达到理想水平。于是就找了几种优化方式。一个是线性缩放位置编码，一个是xPos（具体可以看看苏神的这个文章），还有一个是直接把频率衰减的10000这个参数翻了50倍。最后发现翻倍的方法简单粗暴最有效。

所以直到现在，整个llama3系列的所有频率参数都是500k。其实现在的大模型中这个参数基本都有微调，比如phi4用的是250k，mistral和qwen2.5用的1000k，deepseek r1用的是10k。

另外，RoPE的使用位置是在Q、K的线性变换之后，QK矩阵乘法之前，在拆分多头的时候，尽量将所有的包含位置编码的通道放到同一个头内部。

还有一种叫ALiBi的位置编码，具体我没有了解，大概就是把某种线性的位置编码，直接加到注意力分数（其实好像是在mask的地方，我的理解是让模型的行为更加贴近稀疏注意力或者卷积）处。这个在图像处理领域用的多，跟卷积位置编码结合起来用。

注意力计算的变种

先行提醒，为什么在各种XXFormer百花齐放的架构下，大家仍然选择的是Transformer最原始的注意力计算形式，还是因为原版的transformer足够强大，足以满足大部分的需求，而且效果足够好（还有就是某些变种很容易NaN或者稍微炼两下loss就往天上飞去了）。

余弦相似度

你是否想过，Q与K矩阵乘法的时候，由于初始化或者什么其它原因，如果Q某行的值很大，K对应的值也恰好很大，那么QK相乘就是一个非常大的数字，此时要是用的低精度浮点计算的话，说不定就是inf到NaN的小连招。事实上，在swin transformer里面就出现了因为个别激活值过大导致其它的像素数据的相似度信息被忽略。

这个时候，就出现了余弦相似度的方法。它的想法是，将每一个文本的语义信息都看作一个向量，在比较相似度的时候，不关心这个向量的大小，只关心向量的方向，也据是将所有的向量缩放到一个超球面上面，使点到原点的距离为1即可。

实现的方式也很简单，就是在QK矩阵相乘之前，将QK沿着最后一个维度，也就是通道方向上进行l2归一化即可。l2 Norm的计算方式我在上面也有提到过。由于QK点乘矩阵中的每一项都相当于是单位向量之间的点乘的结果，那么其取值范围其实已经被限定在[ -1, 1]之间了，因此理论上来说不需要再使用scale进行缩放（但是我的实验结果表示使用 $\frac{1}{\sqrt dk}$ 的效果会好一点点）。

当然余弦相似度虽然能够避免某些问题，但是同时也带来了信息丢失的挑战。就比方说前面介绍的RoPE位置编码就依赖于向量的长度，要是使用余弦相似度的话那就用不了这个了。它是具有注意力的机制存在，但是效果就不一定了。

用pytorch实现的时候不要使用nn.MultiheadAttention，因为它包含了QKV的线性变换。

然后就是题外话了，笔者在写余弦相似度的时候偶然想到，可以使用加法代替矩阵乘法，也能计算两个向量之间的相似度，尤其是这种向量长度固定的余弦相似度，取值范围分别是[-1,1]（向量点乘）与[0,2]（向量相加）

笔者借用pytorch的广播机制实现了这一点，但是很遗憾的是，由于广播相加并不像矩阵乘法一样能够融合相乘与累加，导致实际占用显存非常巨大。理论上可以通过重载autograd来实现手动求导，但是笔者懒得写了，没法说明这个方法实用不实用，可不可行。

线性transformer

通读transformer结构，如果你是一个擅长计算模型复杂度的人，那么你立刻就会发现：QK的矩阵乘法随着序列的变长，其所需要的计算量，以及存储注意力分数矩阵所需要的显存大小的增长速度是随着序列长度的平方增长的。如果是线性的系统，那么假设计算8192长度的序列就需要8192倍的1长度所需计算量，但是如果是二次的，那就需要8192 x 8192 = 67M倍的1长度计算量了。要是模型的长度是所期望的“长文本-128k”长度，那这速度能快吗？

于是就有这么一个想法：想保持全局注意的优点的同时，还想要减少计算量或者显存大小，最好把它优化成线性的。

第一个叫Linear Transofrmer。它首先是去掉了对QK矩阵的softmax，并把它替换为一个激活函数（比如ReLU）分别对QK进行处理。式子就变成（暂时省略其它的项）：

$f(Q,K,V)=\phi (Q)\cdot \phi(K^T)\cdot V$

然后发现后面两项可以结合，先计算K与V，由矩阵乘法的规则可以得出，KV矩阵相乘的结果是一个形状为[ channels, channels] 的矩阵，而通道数是固定的，因此此处的空间复杂度直接降到O（1）去了，与序列长度无关，而且接下来Q与后面的相乘，其计算复杂度也变成线性的了。也就是：

$f(Q,K,V)=\phi (Q)\cdot (\phi(K^T)\cdot V)$

虽然总体的计算复杂度依然是二次的（因为KV相乘还是与长度有关），但是相比原本的QK二次、Score V二次两个二次复杂度来说还是有优化的，重点是显存占用是实打实减少了，也确实有全局信息在里面。（注意坐标轴是log的）

代价是，效果没有原本的好。

其实我觉得，单从计算操作上来看，Linear Transformer求解到的是通道间的相似度关系，然后与Q相乘输出。这个操作对自然语言处理意义不是很大，倒是对图像处理方面提供了一定的全局信息，所以也是在图像领域用的多，比如这个超牛的MIT EfficientViT。

图像领域有一个类似的早期简单注意力机制，叫SEBlock，就是先挤压再放回的结构。它是直接提取每个通道的最大值或者平均值，然后linear处理一下，再用类似门控的思想sigmoid一下乘回每个通道。SEBlock提取的就是每个通道的最大值或者均值作为特征，而这个Linear Transformer用的则可以看成是以通道相似度作为特征。

还有LinFormer，LongFormer（这个还可以）等等，想了解就自己看看吧。

在末尾给个苏神的引用：

线性Transformer应该不是你要等的那个模型https://mp.weixin.qq.com/s?__biz=MzIwMTc4ODE0Mw==&mid=2247537863&idx=1&sn=6770fddf32064ef8d004d26001edf527&chksm=96ea8b47a19d0251fc2789d2c9c2c52b64ef2c2c4754f9633fa8575dcb81170d6719cb5e4eef&scene=21#wechat_redirecthttps://mp.weixin.qq.com/s?__biz=MzIwMTc4ODE0Mw==&mid=2247537863&idx=1&sn=6770fddf32064ef8d004d26001edf527&chksm=96ea8b47a19d0251fc2789d2c9c2c52b64ef2c2c4754f9633fa8575dcb81170d6719cb5e4eef&scene=21#wechat_redirecthttps://mp.weixin.qq.com/s?__biz=MzIwMTc4ODE0Mw==&mid=2247537863&idx=1&sn=6770fddf32064ef8d004d26001edf527&chksm=96ea8b47a19d0251fc2789d2c9c2c52b64ef2c2c4754f9633fa8575dcb81170d6719cb5e4eef&scene=21#wechat_redirecthttps://mp.weixin.qq.com/s?__biz=MzIwMTc4ODE0Mw==&mid=2247537863&idx=1&sn=6770fddf32064ef8d004d26001edf527&chksm=96ea8b47a19d0251fc2789d2c9c2c52b64ef2c2c4754f9633fa8575dcb81170d6719cb5e4eef&scene=21#wechat_redirect当你在想“哇！O（1）的空间复杂度好厉害”的时候，现实却不是这样的。在序列长度较短的时候，前面的sdpa计算都是小矩阵乘小矩阵，很快就算完了。

FlashAttention

既然上面的各种尝试都是以模型效果作为代价的，那有没有既可以提速，效果也不减的呢？有。他叫flash Attention，让各大模型的最大上下文长度从2k、4k一点点，直接膨胀到32k起步甚至出现了128k。

通透理解FlashAttention(含其2代和第3代)：全面降低显存读写、加快计算速度https://blog.csdn.net/v_JULY_v/article/details/133619540https://blog.csdn.net/v_JULY_v/article/details/133619540https://blog.csdn.net/v_JULY_v/article/details/133619540https://blog.csdn.net/v_JULY_v/article/details/133619540

flash attention没有改变任何的模型结构，它是纯靠优化算法，硬生生将速度拉起来的，所以模型的效果不会发生改变，但是计算速度就翻了几倍。Flash Attention从硬件下手，发现计算sdpa的时候，它是并行一次性计算好整个注意力矩阵，再并行一次性计算整个注意力输出。对于显卡而言，长序列的注意力分数矩阵是非常庞大的，整个缓存塞不下，就只能放进显存里面计算了。

缓存对计算速度有多大的影响呢？如果你了解过CPU，就直到现在玩网游就有这么一类CPU一骑绝尘，AMD的X3d系列。其原因就在于它把缓存开的够大，计算时想取得数据的时候直接就在高速的缓存里面获取，而不需要走过pcb受接口限制从内存里面到处移动数据。无论CPU还是GPU，最喜欢处理的就是缓存塞得下，而且全部原地操作不需要找内存搬来搬去的数据。

flash attention就是注意到这个问题。它首先发现限制计算速度的主要因素就是缓存与内存之间频繁的数据搬运。一个数据从最开始，QK矩阵乘法搬过去再搬回来，中间Mask、Softmax、Dropout又是搬进来再搬出去，最后与V相乘又搬进来，再搬出去。如果序列长度更长，缓存放不下的话，每一步花在计算上的时间还会更长。flash attention就觉得，应该是有办法能够让矩阵的信息搬进来一次，处理完成以后，再搬出来一次，这样在显存读写，搬来搬去上浪费的时间将大大减少。

具体的实现我并不打算过多阐述，详细内容可以查看文章链接。大致就是将矩阵进行分块，一次性求解一部分的注意力输出，并处理好softmax问题即可。让更多的时间分配在计算上，而不是显存与缓存之间的通信上。如果是使用pytorch框架的话，pytorch在2.0之后原生支持了flash attention2.0的使用，只需要使用nn.functional.scaled_dot_product_attention()函数，代替整个自注意力部分即可。不过需要注意的是，需要自行拆分多头，没有做到nn.MultiheadAttention的封装。

GQA、MQA

还记得前面在线性优化中所说的吗？线性层的开销（在前馈神经网络处，在生成QKV的线性变换处）在序列没有达到一定长度的时候，是远远大于注意力开销的。那么既然注意力开销动不得也没必要动，那就去改一改线性层的开销。在所有的线性层中，改前馈神经网络似乎已经没啥可改的了，从Transformer原本的4倍缩放减到原来3倍甚至2.5倍，再减下去就过多影响模型容量了，而且这也不是什么创新点。那既然不动FFN的话，是不是可以从生成QKV的线性变换上做文章？

有点类似卷积里面的分组卷积，MHA（多头注意力）就类比为卷积中组数为1，MQA就类比为深度可分离卷积，而GQA则类比为折衷的分组卷积。

这个的意思是，比如我输入是2048通道的，拆分为同上图的8个头，要是按照MHA来计算的话，就需要3（QKV各一个）x2048（输出）x2048（输入）的线性变换，然后将输出的三个2048拆分为三个8x256的头。那么我此处的参数量与浮点数计算量都是3x2048x2048。

那我现在的做法是，我假设我的Q提出来的问题有通解，那岂不是很多个问题可以询问同一个键，然后获取这个键的值吗？这样一来，我就可以节省一点生成K和V的线性变换，减少参数量的同时减少计算量。就以上图为例，那么原本的MHA可以被看作为group=head=8，也就是分8组，每组的KV对应1个Q。第二幅图的GQA可以被看作group=4，每组KV分配2个Q，而第三幅图的极端情况，看作是group=1的，每组KV分配8个也就是所有的Q。（这里的group与卷积的group从计算量角度上看还正好相反）

对应的计算量分别是：

GQA（g=2）=2048x2048 + （1024x2048）x2 = MHA x 0.66667

MQA（g=8）=2048x2048 + （256x2048）x2 = MHA x 0.41667

原文给出的性能图表是64头的：

为什么图表中的计算加速比理论上的还要快那么多？这涉及kv缓存的问题，稍后会提及。

这样贪下来，实际表现肯定有损失，但是这个损失是建立在模型大小相同的情况下的。如果GQA省下来的时间与参数量被拿来扩大模型的规模，那么它的表现说不定会更好。而实验的结果也是如此。

XXL大小的模型经过GQA后，其速度提升甚至超越了MHA在更小规模上的速度，而其表现损失也是完全可以接受的。换个角度来说，GQA损失了少量的表现，但是把更大的模型更好的表现下放了到小模型的开销上面。

现在几乎所有的大模型使用的都是GQA，可以说明它确实效果显著。

最后，虽然原文没有提及，但笔者认为在搞GQA的时候要把包含位置编码的QK单独领出来做一组，保证至少在位置编码上不会混杂其它的东西。笔者看过的几个大模型都没有这么做。

GAU与FLASH

首先说明，这里的FLASH其实与flash attention是不一样的意思。GAU与Flash是同一个论文《Transformer Quality in Linear Time》提出来的架构，文章很有意思。

首先是GAU，名字与GLU相差一个字，L表示的是Linear线性变换，而A在此处指代的就是Attention。也就是说，论文把现在常用的模型结构里面，多头注意力模块与后面使用的门控前馈神经网络模块合并在了一起，形成了一个计算量与参数量都差不多的融合模块，就是GAU。

GAU的模型结构如下：

其中，Dense指代的就是pytorch里面的Linear线性层，梯形表示通道数量的缩放，就跟前馈神经网络的那个一样。

模型将整个自注意力模块作为门控的分支（可以说是替换了SwiGLU的SiLU分支）。而这个自注意力模块也是经过一些改动的。

首先，在经过QK的线性变换的时候，它先将输入x的高维的通道变换到更低的维度去，记作Z。而QK则是Z经过通道间的大小缩放与偏置形成的，并非使用线性变换层（有点像层归一化可学习参数里面的gamma与bias）。而且在这里，GAU并没有使用多头注意力机制，而是发现一个头的相似度已经足够好用了（可能与低秩陷阱有关，后面会说）。

接着QK矩阵相乘得到矩阵QK以后，它不进行softmax，因为在其它的早期研究中，有人指出softmax其实并不是transformer之所以有用的重要组成部分，所以这里就换成了ReLU方。图中的QK所加的那个B其实是位置编码以及掩码。进行这样的操作以后，就得到了自注意力分数矩阵。

剩下的操作基本没有太多不同，分数与V相乘，输出形状就是高为序列长度，宽为V的维度（也就是经过线性变换变成高维通道数的V）。然后作为门控与另一个张量相乘，再缩放回原来的维度。

最有意思的是它的实验结果：

实验发现，无论是GAU往多头注意力上靠，还是多头注意力往GAU的方向改进，他们的表现都会变差。也就是GAU的这些改动真的跟组合技一样，只有合在一起才有这样的效果。

堆叠GAU形成的模型在原文中被成为Flash-Quad，在相比原本transformer（+rope+GLU）提高了速度的同时，保持甚至超越了它的表现。

接下来是GAU的进一步版本，FLASH，将复杂度讲到了线性。

首先，Flash改进的是注意力部分，它的注意力包含了两部分的注意力，一个是GAU注意力输出（也就是下面公式中的V quad），另一个是线性注意力输出（也就是V lin）。为了保证GAU的输出不要带来更高的复杂度，所以将它的作用范围进行分块。这有点像swin Transformer的窗口注意力，每个GAU都只负责有限部分的长度的单词。而长距离依赖，则需要靠先行注意力来解决，这里的线性注意力与前文的Linear Transformer差不多。它的式子如下：

论文里面还提到了需要对这些求解结果进行某种缩放，可以看看苏神这个文章里面有集中讨论了这个。

表现非常亮眼（Transformer++就是tr+rope+glu）。可以看到长序列上它的巨大优势。

纯编码器模型（encoder-only）

说到纯编码器，就不得不提到bert，被称为nlp领域的resnet的网络。这里先说明一下为什么这样说。

在图像领域，通常将整个网络分为骨干与头这两部分。骨干用于提取特征，头用于适应下游任务。就拿著名的网络YOLO来举例。在YOLOv8中包含图像分类、目标检测、旋转目标检测、关键点、开放词汇检测、语义分割等下游任务，但是网络在提取特征的阶段，它们的目标都是相同的，那就尽可能地将原图的像素数据转化为深层的特征。这个提取特征所使用的这一部分网络就被叫做骨干。

这时候就有人想到，既然大家的骨干网络都是一样的，那我能不能只训练一个骨干网络，然后大家根据骨干网络提取出来的特征再接上下游任务呢？或者说，能不能让骨干专心于提取特征，不要被下游任务所影响，从尽可能多的方面发现特征，然后再交由后面的头来处理这些高度提取的特征呢？

在图像领域，resnet大概就是这样一个作用（这个网络真忙），YOLO有拿它当主干的版本，RT-DETR有拿它当骨干的版本，ViT-H也是一个ViT前面放个它。前面放个resnet，后面加个代码块，就能完成改变任务目标，迁移学习的作用。Bert要干的也是这个，从大量语料样本上面学习到自然语言内在的逻辑，然后如果是读取然后生成的任务就在后面加个transformer decoder，如果是文本分类就直接放MLP，如果是查找答案就接其它的模块等等。总而言之，就是搞一个能够理解语义信息的骨干网络。

Bert的架构其实非常简单，就是将原始论文的encoder单独拿出来，改成可学习位置编码，然后单独调了一下超参数改了层数通道数等。它的价值应该主要集中在训练阶段。

首先是bert的预训练阶段。在这个阶段里，bert将会使用无监督学习大量的文本，在完成简单任务的同时，逐渐建立起最基础的自然语言逻辑。这里，bert使用“完形填空”来学习单词上下文语义，使用“判断前一句与后一句是否是连续的”来学习句子之间的逻辑联系。

这两个任务的特点就是，它并不需要人为的数据标注就能让模型自己学习到特征，给多少就能学多少，不像图像领域花钱叫一群人来打标（虽然图像领域也有随机mask黑块的训练方法，但是这个貌似就是学的bert的）。

即使是这样的简单任务，也有一定的小技巧。在“完形填空”任务中，有大约15%的文本会被标记为需要被预测的。其中的80%会被标记为特殊的mask字符，表示这个词被屏蔽了，是模型学习的核心。10%的字符保持不变，但是依然需要模型去预测，这能保证模型在学习的时候，不会说attention过几层，某个位置的单词会被其它位置的单词语义给替代掉，保证每一层在每个位置上的单词依然表示的是原来那个位置单词的意思。最后有10%的字符被随机文本替换，也就是它大概率是错误的，增加输入是错误词汇时，模型也能从上下文正确猜出这个词的真正意思。

当然作者的对后面两种的解释就是，在后续微调任务里，mask字符是不会出现的，所以要给点“错误改正”与“背下句子”的任务。

然后是训练的“微调”阶段。此时经过预训练的网络已经学习到了丰富的文本含义，接下来该为下游任务服务了。比方说笔者上中学时期就出现的“英语作文自动打分”任务，从端到端来看就是输入是一个文本序列，输出则是具体的分数。那么只需要在前面预训练的bert后面接上一个对通道的maxpool或avgpool（常见于cnn的图像分类模型），然后放个线性层然后sigmoid+缩放到0到100分即可。

预训练+微调的训练模式也成为了后续训练语言模型的常规方法。就比如GPT-3就是经过大量文本数据预训练出来的模型，而后面的GPT-3.5/chatGPT就是由预训练模型经过特点数据进行微调得到的，它的效果可以说是开创了整个LLM的浪潮。而现在在下载模型的时候，也经常看到有很多的后缀名字，除了有些表示量化的以外，还有的像-base，-instrcuct的后缀。前者表示经过大量文本直接学习出来的模型，后者则代表经过筛选后的文本微调后，更贴近日常使用的版本。

纯解码器模型（decoder-only）

终于来到纯解码器模型了。如果你曾看过语言模型相关的统计图的话，就会发现现在耳熟能详的大模型，甚至每天都在使用的语言模型，绝大多数都是这种decoder-only的架构。decoder究竟有什么好的，值得大家宁愿直接抛弃整个看似合理的encoder，转向只剩一半的transformer呢？

在开始之前，我们需要先了解一下纯解码器模型与原本的transformer-decoder有什么区别。

首先，由于没有编码器，那么来自编码器的交叉注意力就是用不上的了，直接砍掉。欸，那也是一个多头自注意力加上一个前馈神经网络（FFN），那这不就跟编码器长的一样了吗？确实这两个从结构上来说确实基本是一样的，但是其中的关键区别就是：序列的文本来源是自回归的，也就是输入模型的文本，来源于前面所有的文本，包括模型上一次的输出，而且在自注意力里面，是包含掩码的。

纯解码器的transformer块结构大概就是如下所示（甚至是拿编码器的图p的）：

这就奇怪了，这不就是编码器加个掩码吗？这掩码还让它不能往后看，只能往前看，不是还不如既能往后看又能往前看的纯编码器Bert或者就是满血transformer吗？其实不是的。这里的因果掩码其实扮演着非常重要的角色。笔者这里只是简单提一点，只能助于理解，详细内容可以参考这篇文章：

【大模型慢学】GPT起源以及GPT系列采用Decoder-only架构的原因探讨https://zhuanlan.zhihu.com/p/625184011https://zhuanlan.zhihu.com/p/625184011https://zhuanlan.zhihu.com/p/625184011https://zhuanlan.zhihu.com/p/625184011第一个就是这样的因果掩码能够强制注意力分数变成满秩矩阵。这里先说一下矩阵的秩是什么。

这里有两个矩阵，一眼看过去，你觉得哪个更加有意义？

$A = \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 5 & 0 \\ 0 & 0 & 0 & 7 \end{bmatrix}B = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 2 & 4 & 6 & 8 \\ 3 & 6 & 9 & 12 \\ 4 & 8 & 12 & 16 \end{bmatrix}$

答案是A矩阵更有意义，因为在B矩阵中，第2、3、4行可以被简单看作第1行乘某个系数就可以直接得到的，或者从每一列的角度看也是如此。真正存储了数值关系的只有一行或者一列，取决于你怎么化简。而A矩阵不一样，它虽然看上去非常简单，但是每一行、每一列之间都不可能被其它的行表示，所以这个矩阵可以被看作每一行或者每一列都是独一无二的。

为什么要按照行或者列的角度来看，而不是用怎么平移来描述呢？简单来想就是，比如矩阵乘法都是按行按列操作的，怎么平移那都不是矩阵的计算操作。

像A矩阵这种每一行、每一列都需要单独描述特征的，就把它叫做满秩的矩阵，也就是其秩为4，而B矩阵这种一行就能描述完整个矩阵的行列关系的，就把它的秩定为1。

或者我们把矩阵改成方程的角度来看。假设按每一行看，一共有4个y那么：

$A:\left\{\begin{matrix} y_1=2x_1\\ y_2=3x_2\\ y_3=5x_3\\ y_4=7x_4 \end{matrix}\right. B: \left\{ \begin{matrix} y_1 = x_1 + 2x_2 + 3x_3 + 4x_4 \\ y_2 = 2(x_1 + 2x_2 + 3x_3 + 4x_4) \\ y_3 = 3(x_1 + 2x_2 + 3x_3 + 4x_4) \\ y _4= 4(x_1 + 2x_2 + 3x_3 + 4x_4) \end{matrix} \right.$

在A矩阵中，我们可以很容易的解得x与y之间的映射关系。但是对于B矩阵，我们发现y1到y4说的都是同一个式子要想解得 $x_1$ 可以由几倍的y1、y2、y3、y4组成是不可能的，因为信息量不够。

简单来说，就是高秩矩阵包含了更多的有用信息，而低秩矩阵包含很多重复的、没什么用处的信息，而模型在推理的过程中，我们也希望模型能够提取尽可能多的有用的信息，也就是希望各种矩阵的秩都是满的。

那如果不出意外的话，这没掩码的注意力矩阵就要出意外了。有研究发现，没有掩码的注意力矩阵，它的秩不会高于多头注意力中，每个头的通道数dk。要解释起来非常费劲，这里就举一个简单的例子。

假设我们非常极端，拆分多头的时候，让头数直接等于通道数量。也就是比如512通道的输入直接拆分为512个头，每个头包含一个通道。你想这一个通道对比相似度，那这比较的还叫“特征”吗？就是Q那边激活值高的匹配K这边激活值高的，这样就算相似了，是不是觉得这个矩阵得到的相似信息似乎考虑的并没有那么全面，得到这个矩阵也没包含什么信息。

再通俗一点解释，假设qk正在询问一只猫的话，那我们不能仅仅依靠“它毛茸茸的”这个维度，把所有“毛茸茸的”东西全部都匹配为“猫”。此时我们对这个相似度矩阵的描述就是：它太片面了。从数学上来说，就是它的秩太低了，没法携带更多的有效信息。

接下来就是掩码的魔法时刻了。因果掩码直接遮住上三角区域，强行将整个矩阵变成了满秩矩阵——这个是全正下三角矩阵的特性。就如同一个序列文本，即使它的头数特别多，但是每一行他都相当于是“在这个时间步上，我比上一个时间多看到了一个毛茸茸的东西”，至于是不是猫已经没所谓了，因为它这个矩阵保底携带了足够区分每一个时间步的信息。因此，掩码可能会让模型没法向后看，但是它能够保证计算出来的注意力矩阵是足够有意义的，能够脱离这个低秩瓶颈。

链接里面也提到了有一个实验，笔者没去细看，大概也是这个意思。

还有另外一个原因那就是KV Cache技术。

当你观察向chat提问的时候，发出去文字后需要等一小会，然后才会获得回复。其中这段时间有一部分是在排队，还有一部分就是模型正在处理你输入的文本。

那为什么轮到它开始生成的时候，它的生成速度那么快呢，随着生成序列的边长，按照上面复杂度的说法，速度不是也应该越来越慢直到无法接受吗？

还要一个问题，为什么在transformer之前，在自然语言处理混的也还不错的卷积，在大模型这里忽然就没人用了呢？宁可使用ALibi位置编码，甚至窗口注意力来近似让模型的行为与卷积相似，也不愿意使用卷积呢？

它的背后是KV Cache。

我们先回过头来看看模型的结构。在多头注意力部分，QKV与O的线性变换操作的元素都是以单个词作为单位的；在FFN的SwiGLU激活函数部分，什么up，down，门控啥的也都是每个单词单独作用的；在归一化部分，最广泛使用的那种LayerNorm或者RMSNorm，也是以一个单词为单位的归一化。换句话而言，这些操作对于每个单词来说都是独立的，单词与单词之间不会互相影响，没有信息交流。唯一会产生信息交流的地方就是transformer的多头注意力模块内部，计算sdpa的时候。

（图源）

由于掩码的存在，上图中上三角矩阵全部都会被屏蔽，那我们就专注看最右侧的那个红色的词。对于前面的词来说，由于是因果掩码，前面的词看不到后面的词。那么这是不是意味着，现在我在末尾添加了这样一个待预测的词，由于前面的不会看到后面的，所以前面的那些词的计算结果与最后面这个词无关了呢？换句话说，我多预测一个词的话，这个词前面的那些得到的结果都是与没有最后一个词相同的，如果我把最后一个词所需要的信息存储下来，就可以省去大量的重复性计算。

这样也可以回答，为什么现在大模型都不在前馈神经网络层使用卷积。卷积的感受视野是随着层数的加深而逐步扩大的，那么到模型深层的时候，卷积所影响到的范围也是非常大的，破坏了前面这种由因果掩码产生的微妙平衡，前一个词会被后一个词所影响，那么再重复使用前面的词，计算结果就不等价了。

接下来看看这个技术需要存储那些必要信息，顾名思义，它只需要存储KV即可。由于前面所讲的，sdpa以外的其它部分根本不会产生跨词的信息交流，也就不必要存储。

注意到，在注意力分数里，红色的部分是与最后一个字相关的元素。但是由于掩码的存在，涉及最后一个字信息的元素现在就只剩最低下的那一行，其它相关的都被掩码屏蔽了。

要计算最下面那一行，所需要的正好是最后这个字求得的Q，以及整个K矩阵。也就是说，在Q与K矩阵相乘的时候，过去时间的（也就是图片中白色的部分）Q是不需要被存储的，但是需要存储整个K矩阵。

到了与V相乘的时候，由于矩阵乘法的前项是按行的，所以前面多少行的计算与最下面的无关。而由于掩码的存在，正好把V中的最后一行屏蔽了，因此在输出的部分，历史信息的计算是不依赖于当前时间步的，也就是白色部分没有发生改变，所以整个注意力分数矩阵的历史信息是不需要被存储的。

到了最后一行，这一行会与整个V矩阵的所有列相乘得到输出的红色部分，需要整个V给存储下来。

接下来我们擦去干扰项，看看在有KV Cache的时候，前向一次推理需要哪些计算。

原本庞大的矩阵计算，现在直接变成了对一个元素几乎是线性的计算，这也解释了为什么即使是超长的序列，GPT这样的大模型也能飞快的吐出下一个词。本质上来说确实是一个二次复杂度的计算，但是大语言模型可以通过KV Cache技术，把这个大矩阵变成自回归的任务，一步一步地慢慢增加序列长度，将生成的文本及时吐出来，让大家看到生成的过程。自始至终，模型都只在对最后一个元素，也就是待预测的最后一个词进行各种操作，前面的再怎么长那也不会太多地影响它的吐字速度。

还记得前面的MHA、GQA技术吗？在那里，我们通过减少KV的头数，以达到减少参数量，增加推理速度的目的。减少KV头数的同时，也是在减少kv缓存的占用，所以GQA相比MHA带来的加速效果比理论计算高了很多的原因也在这里，它减小了模型对kv cache造成的对显存读写产生的压力。

以减少超长序列的计算量，也是为了减少超长序列的显存占用，是不是有一种方法能够从kv cache上下手，像局部注意力一样，稍微少存那么一般的kv数据也能保持一定的效果呢？有的，但是我不在这里细说了。具体可以看看这篇文章：

大模型百倍推理加速之KV cache篇https://zhuanlan.zhihu.com/p/685853516https://zhuanlan.zhihu.com/p/685853516https://zhuanlan.zhihu.com/p/685853516

接下来我会介绍一个理念与一个算法。

首先，我们知道大模型是靠自回归进行输出的，但是正如成语“胸有成竹”所说，你预测这个词看不到后面的东西，多少还是不合理的吧。于是介绍一个概念，叫束搜索。

束搜索的概念笔者个人感觉是跟大模型无关的。它是这样假设的：当前预测的最佳值，在长远来看可能并不是最佳。每一次都选择概率最高的那一项一般会是一个比较不错的解，但是要想得到比贪心出来更优的解，就需要一定范围以内的搜索了。

举个例子，如果你让一个大模型去随便说一个四字成语，那么它在生成第一个字的时候就会犯难，四字成语那么多，根本没有什么合适的第一个字。而生成完第一个字以后，模型的行为就转换成“成语接龙”的形式了，给定第一个字，预测下一个字。玩过成语接龙的朋友都知道，随便想一个四字成语可比成语接龙简单多了，那把简单的任务困难化，这表现能好吗？

束搜索会先规定：要搜索多深，要保留几个。在每一次推理的最后一步，模型会在选择合适的输出之前，将输出经过softmax转换为概率分布，那么概率靠前的那几个里面，在未来是比贪心算法得到的解更优的可能性会相对较大，所以在这一步，假设我们把这前4个预测字全部保留，再到下一次预测中全部拿去预测新的结果。

新的结果包含了更多的预测结果，四个预测字各自给出了各自的概率输出，在这更多的结果里面，我们依然保留概率总和最大的前四个。循环执行几次，我们很可能就搜索到一个比原始贪心搜索出来的更好的答案。（图源）

束搜索的理念一定程度上利用了未来的信息去影响过去的字，可以达到更好的预测效果，不过缺点也挺明显的，就是计算量翻了几倍。

另一个算法是与深度学习没有关系的，最优控制算法MPC，用于自动驾驶中，控制车的实时速度让汽车能够贴合预先规划的路径上。详细可以看看：

MPC（模型预测控制）原理及理论推导https://blog.csdn.net/qq_37705385/article/details/139030062https://blog.csdn.net/qq_37705385/article/details/139030062https://blog.csdn.net/qq_37705385/article/details/139030062MPC的原理其实与深度学习的训练过程有点像，假设有一个预先规划的轨迹，还通过对路线的时间分配找出了几个路径点。我想要我的运动控制最优，其中不仅包含了车辆对曲线的拟合程度，还要考虑车的转向会不会有问题，以及我更希望车能够越快达到目标点越好。

于是，我们就会对车在未来的时间点（前面时间分配对应的路径点）设计损失函数（当然最快的方式是转化为其它问题求解，但是梯度下降法大家都懂，所以就这样设计了）。损失函数需要包含对车转向的损失、速度太慢也有损失、与轨迹不贴合也有损失。然后简单进行梯度下降求解，求解出来大概就是下面红色的曲线。

这个时候，MPC的关键来了，它只负责从起点到最后一个点的最优控制，并不涉及再往后的点。我们只选取求解出来的第一个点的速度作为当输出速度，但是下一时间步中则要重新计算MPC，而不是直接使用第二个点的速度。第一个速度能够保证在接下来预测的t时间内的路径里面，这个速度就是最优的一部分，但是后面的速度就保证不了是最优的了。剩下的速度倒也不是全部舍弃，它可以作为下一个时刻MPC预测的很好的初始化值。

笔者觉得这个操作与束搜索的思路非常相似，它不同于束搜索，不需要对每种输出单独预测，也不会直接采纳得到的所有输出。它能够持续地保证当前的输出在一定范围内都是最优的。在模型的实现中，就是在末尾不仅仅添加一个待预测的占位符，而是几个，相互之间没有掩码。但是在输出的时候，依然是只预测下一个词，剩下的词在某些实现中（没找到论文）是直接舍弃的。

不过这样的计算量开销也是跟束搜索是一样大的。

笔者这里想到一个没有经过验证的想法，那就是依然保留它们当作kv cache，虽然存储的信息已经过时，但是总比没有好。待预测的词与最后一个词会有信息交流，其余的全部按掩码处理。大概就是下面这张图的形式：

这样的话，即使包含未来的信息并没不都是最及时准确的信息，但是相信模型不会在意这一点，有总比没有要好。而无论预测多远的未来信息，它的计算量始终只是两倍而已，不会像束搜索那样预测多远就多翻几倍。

低秩微调（LoRA）

前面说过，现在的语言模型基本都遵循预训练+微调的训练模式。预训练的模型各家纷纷开源——模型都是几百行（不算并行代码的话）就能描述干净的，数据集都是网上有啥练啥的，只要给出成本去训练，开出来丰富下自己的生态不好吗？真正决定模型效果的，还是那些经过清洗后的，适合用作训练语料的宝贝微调数据集，微调后的产物。

然后呢，有的人就想要拿这个预训练模型来用，给上自己的数据集搭建本地知识库啥的，搞些下游任务，这个过程可不是动动手指调调温度改改topk就能解决的，炼丹是要炉火的。但是吧，这些大企业开源的模型动辄就是多少B的大小，光是部署就很费劲，现在还要多batch进行训练，就以个人开发者或者小型企业来说，这根本吃不消，调不起。

或许就是由于这样的烦恼（或许不是），低秩微调（LoRA）横空出世。

在前面，我讲过矩阵的秩，秩表示矩阵包含的信息量的多少，秩更低的时候它所包含的信息量就会更少。但是，这是否意味着，低秩的矩阵对总体的影响很小呢？那也不是。

这里我简单简单介绍一个有意思的东西，叫SVD非奇异值分解。首先我们需要知道的一点就是，两个矩阵的乘法，M矩阵是a*b的大小，而N矩阵是b*c的大小，矩阵乘法的结果是a*c的矩阵O。但是矩阵O的秩不会大于b。也就是说，1*4矩阵与4*1矩阵乘出来的矩阵，它的秩最大就是1。

SVD分解大致就是将一个高秩矩阵，分解为几个低秩矩阵的和。比如前面使用过的两个矩阵：

A被分解为：

$7\times \begin{bmatrix} 0\\ 0\\ 0\\ 1 \end{bmatrix}\times \begin{bmatrix} 0 &0 & 0 & 1 \end{bmatrix} + 5\times \begin{bmatrix} 0\\ 0\\ 1\\ 0 \end{bmatrix}\times \begin{bmatrix} 0 &0 & 1 & 0 \end{bmatrix} +3\times \begin{bmatrix} 0\\ 1\\ 0\\ 0 \end{bmatrix}\times \begin{bmatrix} 0 &1 & 0 & 0 \end{bmatrix} +2\times \begin{bmatrix} 1\\ 0\\ 0\\ 0 \end{bmatrix}\times \begin{bmatrix} 1 &0 & 0 & 0 \end{bmatrix}$

B被分解为：

$1\times \begin{bmatrix} 1\\ 2\\ 3\\ 4 \end{bmatrix}\times \begin{bmatrix} 1 &2 & 3 & 4 \end{bmatrix}+0+0+0$

注意到排序，靠前的都是常数项较大的，表示靠前的低秩矩阵对原本的矩阵影响最大，而靠后面的常数项稀疏最小，表示他们的贡献更小。

类似的操作还有JPEG的有损压缩算法。总而言之，就是低秩的东西并不一定是没用的。相反，高秩的矩阵可以被拆成低秩的矩阵，那么只要将高秩矩阵中取决定性作用的那些低秩矩阵组成单独拿出来，对它进行微调，不就可以节省大量的过程了吗？

将矩阵分解然后拿出来显然不是机器学习的常用做法，实际的做法是学习这个低秩矩阵的残差，然后训练完以后加到原始矩阵上去即可。

这个就是LoRA的中心思想，上图左侧的蓝色线性层的权重矩阵我们给他冻结，这样反向传播的时候就不需要对巨大的矩阵求解梯度，也不需要额外消耗显存记录这一侧前向传播的张量。

LoRA主要解决了显存不够用的问题。就简单拿一个7b-f16模型，30层2k通道，512长度上下文，标准tr+swiglu的配置进行计算。如果是全量微调，即使是最原始、效率最低的SGD优化器，单是将参数塞进显存就要14G，然后需要记录流过的所有张量，粗算了下也要43.2G每批（实际这里会更多，因为我没有计入激活函数前后、以及整个sdpa的中间张量，因为有些数据需要更高的存储精度）。记录梯度需要更高精度的单精度浮点就是28G。也就是说，即使是最基础的1batchsize训练，从启动开始就需要吃掉51.6G显存，而能放下这个数据的最实惠的配置，一张A6000（需要AMP，价格上平台搜一下就知道了，离谱）。如果是使用能够超速训练的优化器（比如AdamW）那么最后面这个28G还将翻翻到84G，这是一张金砖A100都装不下的。

但是如果将中间的每一个矩阵都使用LoRA进行微调的话，将一个2k*2k的矩阵转化为2k*16*2的话，从需要梯度的参数量上，就能节省到原来的1/64。换句话说，它所需要记录的梯度占用将会大大减少，即使是AdamW优化器，现在部署门槛也变成了14G+1.2G+1.3G=16.5G。这个是什么概念？原本需要大价钱购置A100的模型，现在只需要一架传奇仙炉2080Ti-22G就能训练，成本降的可是比显存降的还多啊。

然而实际上，LoRA并不会对ffn进行微调（因为没有找到微调ffn的实验，笔者自己也没有做实验的能力）它只需要学习QKVO的权重矩阵就能达到足够好的效果。这或许也侧面证实了，ffn主要存储的是知识，而QKVO矩阵主要存储了模型的思维形式或者语言风格。

不过这也引入了一个担忧，那就是那么低秩的矩阵真的能有效吗？事实上，前面的rank=16已经是相对来说较高的秩了。下面是对GPT-3的175b参数量进行微调的实验结果：

面对即使175b的参数量，LoRA在即使仅微调V矩阵，仅使用秩为2的矩阵，仅仅4.7M的参数量（3.7万分之一的参数量！）就能达到接近于甚至超越全参微调的效果，非常震惊。

作者认为，LoRA所训练的低秩矩阵的作用，是放大了那些与下游任务相关的特征，同时保留其它特征的存在。

LoRA的公式为：

其中 $W_0$ 指代的是原始参数矩阵，B、A指代的是低秩的参数矩阵，矩阵相乘的结果就是低秩矩阵。下面的r指的就是矩阵的秩，上面的α是一个缩放系数， $\frac{\alpha}{r}$ 的值按经验取2，在反向传播的时候相当于对矩阵进行缩放。按照某些说法，较大的缩放值能够让训练加速（类似于学习率那种），更快的适应新任务，而较小的缩放值则会更有助于泛化（笔者觉得不如调学习率，反正要学的东西都在这里面）

LoRA的另一个特性就是，在微调完成的时候，导出模型时，两个分支的矩阵是可以合并的，不会因为加了参数微调而改变速度与参数量占用。它相当于使用低秩的矩阵拟合了预训练矩阵与目标下游任务之间的残差。

模型蒸馏

一般来说，大家都会默认的一个点就是模型的参数量越大，那么模型的能力就会越强。405B的模型在架构相同的情况下，是一定比36b的小模型的表现更好的。

真的如此吗？

其实Qwen家族从1代到2.5代变动其实很少，但是在同样参数量的情况下，它的效果就是每一代都在提升。

甚至还有3b打14b的情况。

在llama2的研究里面发现，相比于大规模的文本微调，更加高质量的文本微调往往能够带来更好的微调效果。而《 Quality is All You Need for Chinese Instruction Fine-tuning》也讲到了其中的重要性。在论文中，研究者发现来自于弱智吧的文本数据能够明显提高模型的推理能力。

但是，世界上只有一个弱智吧，但是有几乎无限膨胀的模型参数量，有几乎无穷无尽的高质量文本需求。何况，使用AI生成的文本拿来训练AI，最后的结果很可能是模型崩溃。

那怎么办？总不能像图像领域那样，雇佣一大群人跟批改作文似的给文本打标吧，一个人看完一本百万字的小说按也要差不多一周，得到的不过是1M的文本数据，那模型训练用的文本量可是按G算的，这标到什么时候去？

是的，最早的模型蒸馏（甚至都不应该叫蒸馏）就是为了解决类似问题出现的。首先花费成本训练一个大的模型，然后让它代替人手去标注标签，然后让小的模型去学习标注过后的标签。图像领域里面那些AI辅助标注软件，比如LabelStudio、TRex label等等。

大模型里面管这个叫数据清洗，其实现在使用的也很多，那就是专门训练一版像bert这样的语言模型，然后判断它的文本质量如何。那些有错误的，或者没有逻辑的文本就会被自动筛选掉，不需要再一个一个看去。现在也有很多大模型的数据清洗就是用的大模型来做（比如GPT3.5）。

但是吧，这样只是使用模型筛选数据，并没有改变整个模型的训练过程，那有没有什么更好的方式，能够让一个模型学习到另一个模型的“知识”呢？这就不得不提到一个更加实用的技术：知识蒸馏。

知识蒸馏常用于小型模型的版本，比如Llama3.1有一个405b的超大版本，虽然能力强但是启动、部署所需要的开销也很大，不适合在资源受限的情况下使用。那么llama就会推出更加小型化的72b、32b、7b等小模型。但是同样的训练数据流过模型容量更小的模型里面，他们未必能够有充足的参数量去精准的把握自然语言中的内在联系，因此通常更加难以取得好的效果。

那么既然已经有了一个405b大的模型，那我能不能直接使用大模型学到的知识，帮助小模型把握其中的内在规律呢？当然是可以的。模型蒸馏的大致流程如下：

知识蒸馏的主要思想就是，让一个庞大的网络叫做“教师网络”，然后将它所学到的知识“蒸馏”到较小的学生网络中。相比于真实标签的独热答案，使用教师网络生成的概率数据显然能够给学生模型提供了更加有用的信息。比方说，当你询问大模型“今天嘉然吃什么？”，如果是使用真实标签，那么就会是“吃饭”这一个答案，那么对于损失求解来说，除了“吃饭”以外的所有答案都是错误答案。然而实际情况是嘉然今天吃什么都可以，已经充分训练过的教师网络显然是知道这一点的，因此教师给出的答案是一个软标签：“有20%概率吃饭，有15%概率吃面，有10%概率什么都不吃……”，那么学生网络就会学习这个概率的分布，使得自己的输出分布将更贴近于教师的分布。

换而言之，学习真实标签是在强记答案，小的模型自然记不住。那么学习教师网络的概率分布，则更像是在学习教师网络学习到的规律，学习规律显然是比学习答案更加合理的。

如果从另一个角度去看待，如果把神经网络看作使用简单操作拟合出来的高维复杂函数，教师网络所做的事情是找到一个函数fx，使得输入文本序列x，输出文本y。而学生网络所需要做的并非文本的匹配，而是直接找到另一个更加简单的网络gx，使得他能拟合教师网络的fx。

这种训练方法有效吗？答案是非常有效，能够极大地减少参数量，减少计算量，同时使得小模型的表现并不会弱于大模型太多。比如在图像领域MobileSam里面，作者直接将632M的巨型图像嵌入网络替换成仅5.78M的超小网络，使用原始数据集SA-1B的仅1%（其实也是超级大）的数据量进行8轮的蒸馏训练。

mobileSam的结果就是，推理速度加速56倍，同时性能不减。对比以YOLOv8-seg为框架的FastSam（在SA-1B数据集的2%上，纯训练）达到更快并且效果碾压的实力。

而最近新出的deepseek-r1其中1.5b到70b都是源于开源的模型，经过自家671b庞大教师模型蒸馏出来的，相比原始模型也是有提升。

（排行榜很多没有更新，图中的deepseek r1-7b就是基于qwen2.5-math-instruct蒸馏671b的模型得到的，其它的模型没有上榜，排名低可能是因为math没有得分）

写在最后

只是笔者忽然间想到一种训练方式。就是每一层transformer层都会产生输出，然后都会产生loss，每一层loss只会反向传播到这一层的开始，这样或许可以让简单的信息压缩到前面的层，而复杂的信息只能在后面的层里被推算出来。理论上来说可以适用于任何可以加入残差链接的层里面，但实际效果如何就不得而知了。