【电路理论三】电路进阶定理

置换定理

在任意线性和非线性电路中，若某一端口的电压和电流为U和I，则可用的电压源或的电流源来置换此一端口，而不影响电路中其它部分的电流和电压。

说明： 

(1)置换定理既适用于线性电路，也适用于非线性电路；

(2)置换定理要求置换后的电路有惟一解；

(3)除被置换部分发生变化外，其余部分在置换前后必须保持完全相同；

(4) 被置换的支路和电路其它部分应无耦合关系。（无受控源影响）

一个例子

齐次定理

在只有一个激励X作用的线性电路中，设任一响应为Y，记作Y=f (X)，若将该激励乘以常数K，则对应的响应Y’也等于原来响应乘以同一常数， 即Y’=f (KX)=Kf(X)=KY。

若电路中只有一个激励，则响应与激励成正比。

用齐次定理分析梯形电路特别有效：

叠加定理

在线性电路中，由几个独立电源共同作用产生的响应等于各个独立电源单独作用时产生相应响应的代数叠加。

注： （1）叠加定理只适用于线性电路，不适用于非线性电路；

（2）在各分电路中，不作用的电压源置零，相当于短路；不作用的电流源置零，相当于开路；

（3）电路中所有电阻和受控源保留不动；

（4）各响应分量叠加时，其参考方向与原电路响应参考方向一致时取正，否则取负；

（5）功率不满足叠加定理。

再来一个例子：

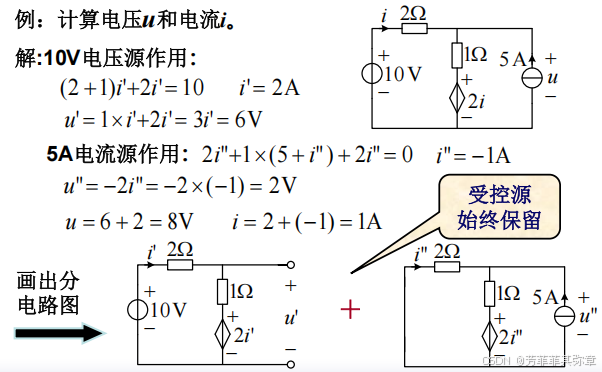
齐性定理与叠加定理

线性直流电路的任一响应可表示为该电路中独立源的线性组合，即：  

注：系数与独立电源无关，由电路的结构和电阻以及受控源参数决定

齐次定理和叠加定理的综合例题：

等效电源定理

戴维南定理

1 定理内容：线性含源一端口网络的对外作用可以用一个电压源串联电阻的电路来等效代替。其中 电压源的源电压等于此一端口网络的开路电压，而电阻等于此一端口网络内部各独立电源置零后所得无独立源一端口网络的等效电阻。

注：

电流源置零=电流源开路

电压源置零=电压源短路

等效电阻的计算方法：

当网络内部不含有受控源时可采用电阻串并联的方法计算；

加压求流法或加流求压法

开路电压、短路电流法

诺顿定理：（戴维南定理的类似）

线性含源一端口网络的对外作用可以用一个电流源并联电导的电路来等效代替。其中电流源的源电流等于此一端口网络的短路电流，而电导等于此一端口网络内部各独立源置零后所得无独立源一端口网络的等效电导。这一定理称为诺顿定理，所得电路称为诺顿等效电路。 

两者一般都可以互相转换，除非特例：

时只存在诺顿等效电路；时只存在戴维南等效电路。