同余式化简计算

加法化简

加法即可以把一个数拆成两个数相加，其中一个数为模数的倍数，剩下一个即化简后的数字。

原理

a=qm+b，求ax≡1（modm）的解，即（qm+b）x=qmx+bx≡1（modm）。m整除qmx，则只需计算bx≡1（modm）的解即可。这里我们可以把b控制在0～m-1的范围，这样就极大地化简了计算量。

例子

比如990*x≡1（mod7）可化简为

（7*141+3）x≡1（mod7）

3x≡1（mod 7）

x=5

乘法化简

乘法同余1的式子可以进行化简

原理:

如果x²≡1（mod a）

则x²=ak+1

x⁴=（ak+1）²=a²k²+2ak+1≡1（mod a）

但是同余其他数不一定能化简

比如x²≡2（mod a）

x²=ak+2

x⁴=a²k²+4ak+4≡4（mod a）

此时x⁴模a余4而不是1

例子

运用欧拉定理x⁶≡1（mod 7），可推出x²≡1（mod 7）

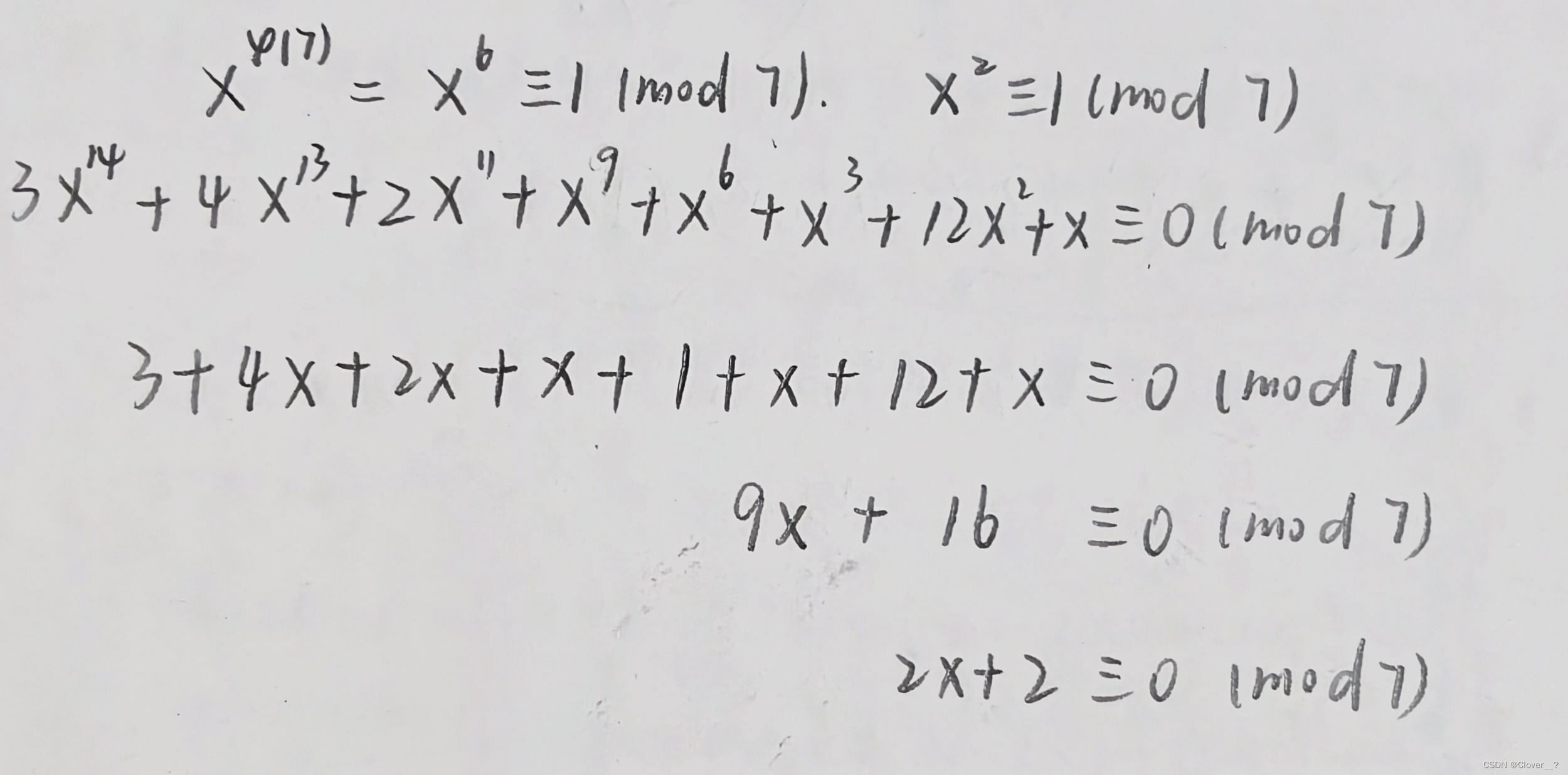
 可计算出x≡6，这种多项式解的范围为0～6，所以一开始要验算x≡0是否符合，综上，解为x≡0或x≡6（mod 7）