数据结构——七、特殊矩阵的压缩存储(王道408)

前言

摘要： 本文介绍了数组的存储结构与特殊矩阵的压缩存储方法。对于一维数组，元素连续存储且支持随机存取；二维数组可采用行优先或列优先存储策略。特殊矩阵包括对称矩阵、三角矩阵和三对角矩阵，通过压缩存储可节省空间。对称矩阵仅存储主对角线和一侧三角区，利用对称性访问另一侧；三角矩阵额外存储一个常量；三对角矩阵按行优先存储带状区域。每种矩阵都给出了下标映射公式，实现矩阵元素到一维数组的高效定位。

代码在本文开头的资源里面,有需要可以自取😋

一.数组的存储结构

1.一维数组

1.一维数组的存储结构

• 各数组元素大小相同，且物理上连续存放。

2.一维数组的随机存取

• 只需要知道一个一维数组的起始地址,我们就可以很方便地计算出任何一个数组下标所对应的这个元素它的存放地址是多少
• 数组元素a[i]的存放地址 = LOC + i * sizeof(ElementType) (0≤i < 10)
• 注：除非题目特别说明，否则数组下标默认从0开始

2.二维数组

1.逻辑结构

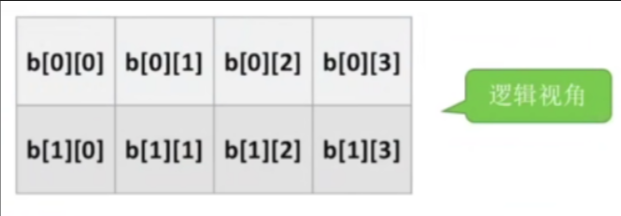
2.两种不同的存储策略

1.行优先存储:先存第一行再存第二行,以此类推

• M行N列的二维数组b[M][N]中，若按行优先存储，则b[i][j]的存储地址=LOC(起始地址)+(i*N+j)*sizeof(ElementType)

2.列优先存储:先存第一列再存第二列,以此类推

• M行N列的二维数组b[M][N]中，若按列优先存储，则b[i][j]的存储地址=LOC(j*M+i)*sizeof(ElementType)
• 我们规定行优先或者规定劣优先的存储原则,其实本质的目的是想要把这样的一个非线性的二维数组,把它拉成一个线性的形状,因为计算机内存的这些存储空间都是线性的
• 可以实现随机存取

二.特殊矩阵

1.普通矩阵的存储

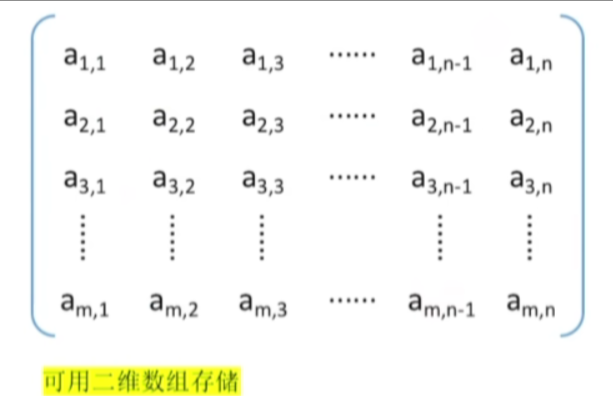
注意：描述矩阵元素时，行、列号通常从1开始；而描述数组时通常下标从0开始
（具体看题目给的条件，注意审题！）

某些特殊矩阵可以压缩存储空间

2.对称矩阵

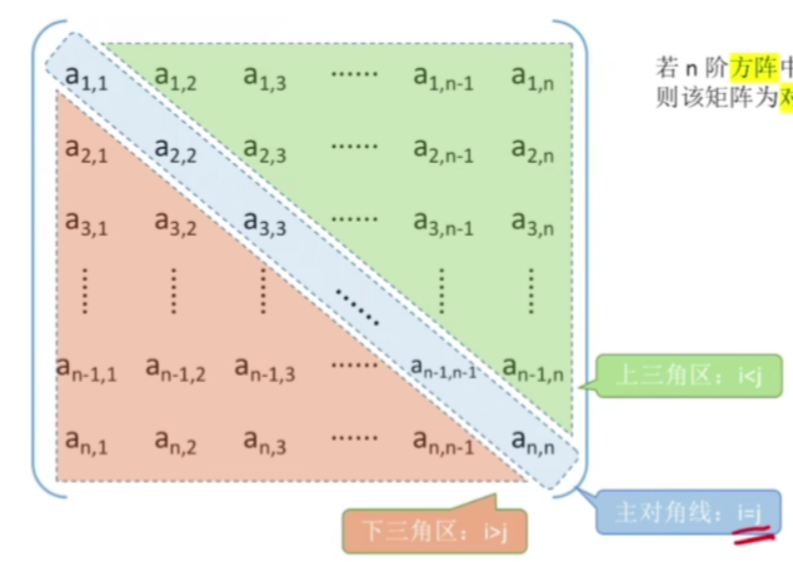
1.定义

• 若 n 阶方阵中任意一个元素 $a_{ij}$都有 $a_{ij}=a_{ji}$，则该矩阵为对称矩阵。

2.压缩存储策略

• 由于对称矩阵的这两个三角区它们的数据其实是完全相同的,因此我们在存储对称矩阵数据的时候,其实我们只需要存储其中的一个部分
• 压缩存储策略：只存储主对角线+下三角区或者只存储主对角线+上三角区

3.按照行优先存储主对角线+下三角区

• 按行优先原则将各元素存入一维数组中

• 所以各个元素在内存中的排列如下图所示
  

• 数组大小可以设置为:$1+2+3+...+n=\frac{(1+n)\ast n}{2}$

• 最后一个数组元素下标为$\frac{n(n+1)}{2}-1$

• 为了方便使用,可以实现一个“映射”函数矩阵下标→一维数组下标

4.行优先的映射函数的实现方法(矩阵下标转数组下标)

• 矩阵下标 -> 一维数组下标
  $a_{i,j}(i>j)\text{->}B[k]$

• 按行优先的原则,i是矩阵行号,j是矩阵列号,所以在$a_{i,j}$的前面应该是有i-1行,而每一行有i个元素,i-1行就有1+2+3+…+i-1个元素,而$a_{i,j}$在第i行的第j列,于是在加上一个j就是$a_{i,j}$的位置,所以$a_{i,j}$是一维数组的第$\frac{i\ast (i-1)}{2}+j$个元素(位序)

• 因为位序是数组下标+1,因此$B[k]$的数组下标k为$\frac{i\ast (i-1)}{2}+j-1$

注:有的题目它的数字下标是从1开始的,此时位序就是数组下标,就无需减1

• 因为i大于等于g这个区域的,所有的这些元素都是按照行优先的顺序依次存到我们的一维数组当中的,所以我们可以直接用这种直接相加的方式就可以找到它在数组当中的实际位置

5.行优先原则访问上三角区域

• 如果要访问的是上三角区的这些元素,也就是i小于j的情况
• 矩阵下标 -> 一维数组下标
  $a_{i,j}(i<j)\text{->}B[k]$
• 这部分的元素,虽然我们没有把它实际存到这一维数组当中,但是由于对称矩阵$a_{i,j}=a_{j,i}$ ,所以其实如果行号小于列号的时候我们可以把它转换成访问对应的$a_{j,i}$ ,这样就又变成了行号大于列号的情况,所以就可以用和刚才相同的方法来算出
• $k=\frac{j\ast (j-1)}{2}+i-1$

6.小结:按照行优先的方式来压缩存储对称矩阵,存储的是主对角线和下三角区

• 把矩阵下标转换为一维数组下标的公式为:
  $k=\{\begin{array}{ll}\frac{i(i-1)}{2}+j-1,& i\ge j\text{(下三角区和主对角线元素)}\\ \frac{j(j-1)}{2}+i-1,& i<j\text{(上三角区元素}{a}_{ij}=a_{ji}\text{)}\end{array}$

7.按照列优先原则存储矩阵

• $a_{i,j}$ 是第 $\left[n+(n-1)+\cdots +(n-j+2)\right]+(i-j)$个元素
• 因此k = $\left[n+(n-1)+\cdots +(n-j+2)\right]+(i-j)-1$

3.三角矩阵

1.分类

1.下三角矩阵

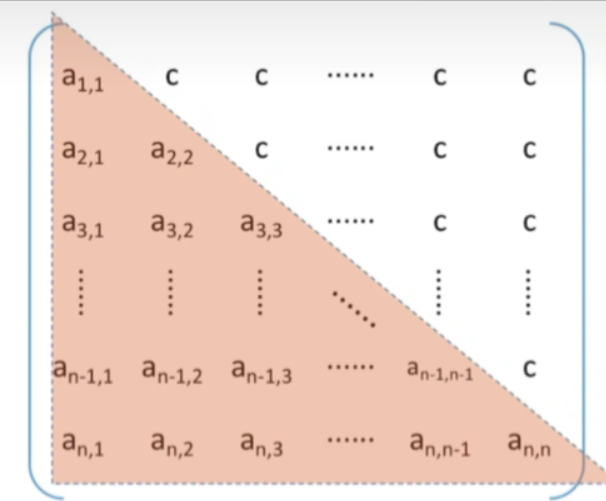
下三角矩阵：除了主对角线和下三角区，其余的元素都相同

2.上三角矩阵

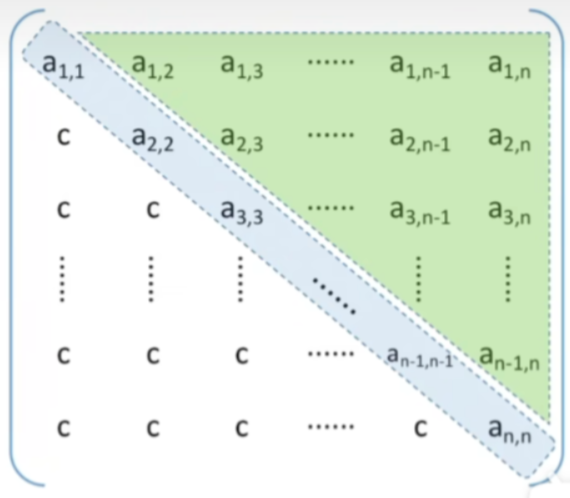
上三角矩阵：除了主对角线和上三角区，其余的元素都相同

2.下三角行列式压缩存储策略

• 压缩存储策略：按行优先原则将橙色区元素存入一维数组中。并在最后一个位置存储常量c
• 相比于对称矩阵来说,存储同阶的三角矩阵,我们需要多存储一个单元

3.存储主对角线+下三角区+一个常量

• 按行优先原则将各元素存入一维数组中

• 所以各个元素在内存中的排列如下图所示
  

• 数组大小可以设置为:$1+2+3+...+n=\frac{(1+n)\ast n}{2}+1$

• 最后一个数组元素下标为$\frac{n(n+1)}{2}$

• 为了方便使用,可以实现一个“映射”函数矩阵下标→一维数组下标

4.映射函数实现方法

• 矩阵下标 -> 一维数组下标
  $a_{i,j}(i>j)\text{->}B[k]$
• 按行优先的原则,i是矩阵行号,j是矩阵列号,所以在$a_{i,j}$的前面应该是有i-1行,而每一行有i个元素,i-1行就有1+2+3+…+i-1个元素,而$a_{i,j}$在第i行的第j列,于是在加上一个j就是$a_{i,j}$的位置,所以$a_{i,j}$是一维数组的第$\frac{i\ast (i-1)}{2}+j$个元素(位序)
• 因为位序是数组下标+1,因此$B[k]$的数组下标k为$\frac{i\ast (i-1)}{2}+j-1$
• 按照前面对称矩阵的计算方法,k的公式为:

5.行优先原则访问上三角区域

• 这个区域所有的元素它们都是一个常量c,因此访问这个区域的任何一个元素,我们都应该把它映射到这个一维数组的最后一个位置所以上三角区的这些元素它所对应的一维数组下标就应该是$\frac{n(n+1)}{2}$.

6.小结:按照行优先的方式来压缩存储上三角矩阵,存储的是主对角线和下三角区

• 把矩阵下标转换为一维数组下标的公式为:
  $k=\{\begin{array}{ll}\frac{i(i-1)}{2}+j-1,& i\ge j\text{(下三角区和主对角线元素)}\\ \frac{n(n+1)}{2},& i<j\text{(上三角区元素}\text{)}\end{array}$

上三角行列式也是类似的
$k=\{\begin{array}{ll}\frac{(i-1)(2n-i+2)}{2}+(j-i),& i\le j\text{(下三角区和主对角线元素)}\\ \frac{j(j-1)}{2}+i-1,& i>j\text{(上三角区元素}{a}_{ij}=a_{ji}\text{)}\end{array}$

4.三对角矩阵

1.定义

• 三对角矩阵，又称带状矩阵：当|i-j|>1时，有aᵢⱼ=0(1≤i,j≤n)
• 所有在主对角线上的元素,可以是非零元素,另外从主对角线元素出发,它们的上下左右与它们相邻的这几个元素,也可以是非零元素再往外的这些元素就肯定是零元素

2.三对角矩阵的压缩存储

• 压缩存储策略：按行优先（或列优先）原则，只存储带状部分
  

• 一维数组长度:对于带状矩阵来说:除了第一行和最后一行只有两个元素之外,其他每一行肯定都有三个元素,所以一个n阶的带状矩阵,我们需要存储的元素个数就应该是3*n-2

• 由于我们这默认数组下标从零开始,因此最后一个元素它的数组下标就应该是3n-3

3.映射函数实现方法

• 如果要访问的这个元素,它的行号和列号差值大于一,那么这个区域的元素肯定就是0
• 矩阵下标 -> 一维数组下标
  $a_{i,j}(|i-j|\le 1)\text{->}B[k]$
• Key: 按行优先的原则，a_{ij}是第几个元素？
  1. 前 i-1 行共3(i-1)-1个元素
  2. $a_{ij}$是i行第j-i+2个元素
  3. $a_{ij}$是第2i+j-2个元素
  4. 因此k=2i+j-3(数组下标从0开始)

4.数组下标k转化为i,j

• 第k+1个元素，在第几行？第几列？

1. 前i-1行共3(i-1)-1个元素
2. 前i行共3i-1个元素
3. 显然，3(i-1)-1<k+1≤3i-1
4. i≥(k+2)/3,可以理解为“刚好”大于等于
5. $i=\left[(k+2)/3\right]$,向上取整即可满足“刚好”大于等于
6. i是行号,所以它肯定是一个整数,因此当i取得$\left[(k+2)/3\right]$的时候,刚好可以满足我们这儿所提到的这个不等式也就可以保证我们这儿要找的这个元素刚好就是在第i行
7. 由 k=2i+j-3，得j=k-2i+3

5.稀疏矩阵

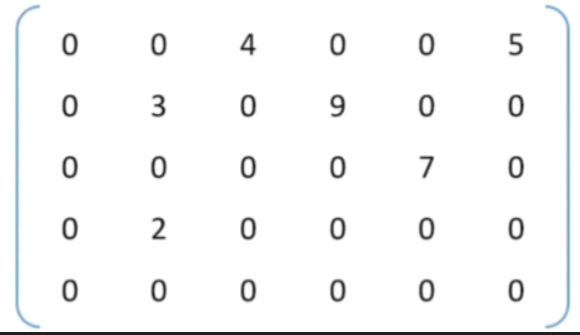
1.定义

• 稀疏矩阵：非零元素远远少于矩阵元素的个数

2.压缩存储策略

1.方案一

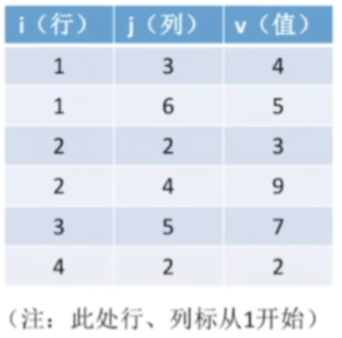
• 压缩存储策略一:顺序存储——三元组<行，列，值>
  

• 在这里边存储的都是稀疏矩阵里边的非零元素

• 代码实现方法:

  1. 定义一个struct
  2. 这struct里边有i有j有value
  3. 一个struct对应上面表格中的一行
  4. 再定义一个和这个struct相对应的一维数组
  5. 就可以顺序的存储这些三元组

• 用这种方式存储系数矩阵,那你要访问其中的某一个元素,只能顺序的依次扫描这些三元组,会失去随机存取的特性

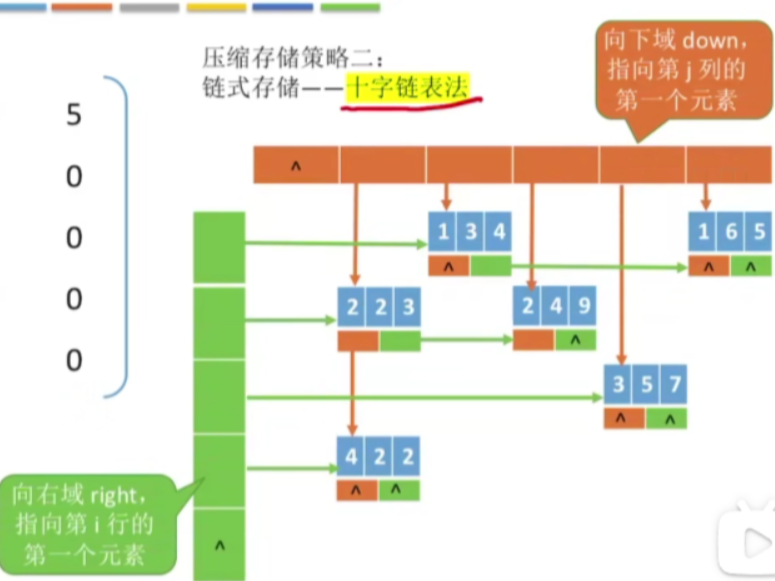
2.方案二

• 压缩存储策略二:链式存储——十字链表法
  

• 定义这样的一个数组,这个数组里面存放的是一个一个的指针我们把这些指针称之为向下域,这儿的每一个指针其实就对应了稀疏矩阵当中的每一列

• 这边我们同样需要定义一个指针数组,这些指针分别对应稀疏矩阵当中的各行

• 每一个非零元素会对应这样的一个节点,这个节点当中包含了非零元素它所在的行列到底是多少,它的值是多少,另外还会有两个指针,一个指向同列的下一个非0元素,一个指向同行的下一个非0元素
  

三.重要考点

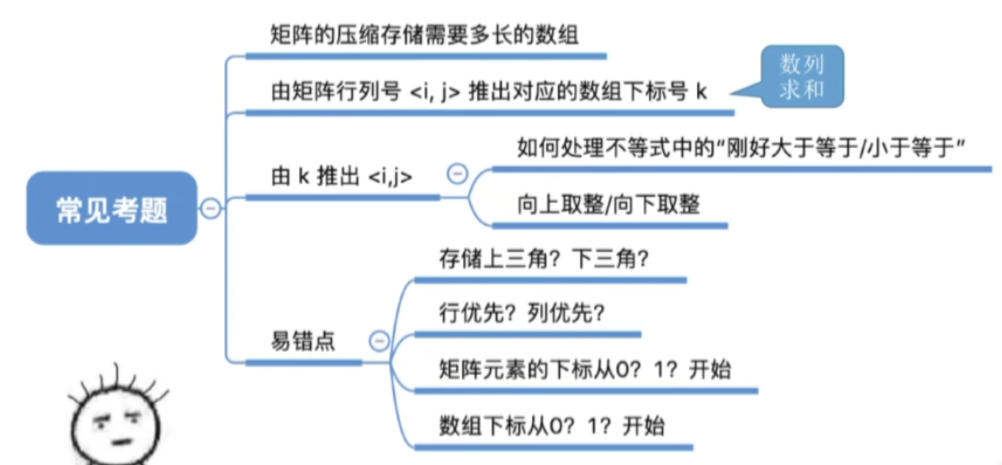
结语

今天实在是太难了😫,既要写二叉树的代码也要写矩阵代码,结构写完二叉树代码已经23:00了😖,没时间了,只能先上传干货了,代码后面会补的😖

文章有公式有一些错漏的地方😥,今天已经自查出来并且改正了😖,后面我会仔细查看文章尽量避免这种情况😁

没想到这个代码这么难写😖,昨天写了一天,今天早上起来又测试了代码,应该无误😉,但是这个代码的时间复杂度实在太差了😫,大部分代码都是$O(n^2)$的,我只能说尽力了😖,现在代码的水平确实不高😥,但是我后面一定会越来越好的😋,这个代码后面没有时间的话应该不会进一步优化了😁,有兴趣就下载下来看看吧,非常欢迎各方大佬对我的代码斧正😉

想查看其余数据结构的篇章?
请点击一、数据结构专栏导航页（王道408）