上一节在讲传递函数的性质时提到,传递函数的极点就是微分方程的特征根,这是本节逻辑链的关键环节。
引言
这一节我们讨论:
为什么要求模态?如何求模态?模态反映了系统的什么特性,有什么规律?
我们从一个例子引入:
解该微分方程并观察解的走势:
先解方程,对微分方程进行拉氏变换:
我们希望得到其在实域中的解,因此要进行反拉氏变换,由于拉氏变换数对表标准形式的s系数都为一,因此对解进行标准化:
进行反拉氏变换,绘制图像:
 (输出响应-时间图)
(输出响应-时间图)
输出响应显然递减,且当t趋于无穷时,输出响应将趋于零。这意味着,系统将在无限长的时间后达到稳态。
可以归纳,所有含的函数都是趋于稳定的。
模态是什么?
在这个例子中,决定函数走向的很明显是,因此我们称在输出中影响走向的项为模态。
为什么要求模态?
别忘了我们系统分析的起因就是希望得到系统的一些特性,模态就是一个很好的工具。
通过例子的分析我们知道可以通过模态得知系统的稳定性。此外,模态分析帮助我们理解系统的自然响应特性,即没有外部输入时系统的自由振动方式。这些模态决定了系统如何响应各种激励,包括它们的稳定性、响应速度和形式等。
在解题过程中你可能会有疑问,为什么要反拉氏变换到时域上求解?
这是因为在频域中是无法建立输出响应与时间的关联的,我们又希望能得到解的走势观察系统稳定性,因此要做反拉氏变换到时域内,与时间建立函数关系绘图。
如何求模态?
模态分析就是分析系统的输出响应与时间的关系,任何系统都可以进行模态分析。
在上一节讲传递函数的时候提到过:
Ⅰ得到传递函数:
任何系统分析都要得到 微分方程,得到 微分方程 后就可以通过 拉氏变换 为 传递函数 求解。
Ⅱ 转化为零极式:
任何传递函数都可以被化简为 多项式函数,因此都可以转化为 零极式。
===>
Ⅲ 裂项或凑数对表:
因而都可以对分母进行裂项,裂项方法和求解方法可以在第一节找到
如果有复数根,则需要对应数对表来凑
Ⅳ 反拉氏变换:
而裂项后的分母都可以通过化简,转化为 拉氏变换数对表 中的形式,都可以进行 反拉氏变换,得到在微分形式下的解!
而在时域(微分形式)中的解就能很好地反映输出响应与时间的关系,观测系统是否收敛稳定。
这就是模态分析的基本流程。
模态由什么决定?
我们依然通过例子引入:

式一:
根据求模态的四步骤,题目已经完成了拉氏变换并得到了输出的零极式,
接着,我们应该对分母进行裂项,从而得到可以进行反拉氏变换的项:
最后通过查表得知解在时域中的形式是:
式二:
同理,。
我们发现,两微分形式解的走势都由e的次幂决定的。由于是代数方程通过反拉氏变换得到的,因此e的次幂与代数方程X(s)的分母相关,与分子无关。
因此可鉴,分母的极点决定了e的次幂,从而决定了解的走势,也就是模态。
而在本节一开始就强调了:传递函数的极点就是特征方程的特征根,因此模态也就是由特征方程的特征根决定的。
那分子影响了什么?
没错,分子影响了这个走势的“程度”,比如本例的a1 a2,分别代表这最终输出中的曲线是更趋向于还是
呢。
至此,我们了解了模态是由微分方程的特征根,或是传递函数的极点决定的。
接下来我们就要研究极点是如何影响模态的,或者说,他们的关系是什么样的?
特征根(极点)与模态的关系
我们从例题出发,感受一下为什么“所有系统都可以进行模态分析”,顺便熟悉一下解题过程。
Ⅰ 特征根无重实根
刚刚提到了,特征根即为模态
的参数α。
Ⅱ 特征根为重根
Ⅰ 利用拉氏变换转化为代数方程:
Ⅱ 转化为零极式:
Ⅲ 进行裂项并求解:
Ⅳ 反拉氏变换得到解的微分形式:
我们发现,有几个重根,微分形式的解的e就有几项。
Ⅲ 特征根为复根
Ⅰ 利用拉氏变换转化为代数方程:
Ⅱ 转化为零极式:
Ⅲ 进行配凑并求解:
Ⅳ 反拉氏变换得到解的微分形式:
我们发现,特征根为复数根的解往往含有震荡项sinβt。
经过这三个例子可以发现,
任何微分方程都可以按根的情况分成三种形式,都可以通过反拉氏变换可以获得对应的三种模态,这也是为什么任意系统都可以进行模态分析的原因。

这张表很明确地指出了特征根(极点)与模态之间的关系:
对于特征根无重实根的方程,其极点-α经过反拉氏变换成为模态的λ参数。
对于有重实根的方程,由于其反拉氏变换,特征根有几重根,
就有几项。极点-α也是模态的λ参数。
对于是复数根的方程,由于其反拉氏变换/
,因此总是有震荡项,极点-α也是模态的λ参数。
通过上文,我们已经构建起极点与模态之间的关系了,进一步,我们希望能通过极点就能一眼判断出系统的稳定性。
接下来,我们建立极点与系统稳定性的关系:
通过极点判断系统稳定性(敛散性)、震荡/阻尼性
直观观察极点是如何影响曲线走势的?
下面四幅图,分别对应了几个微分形式解的输出响应-时间图,可以直观观察出系统的稳定性:
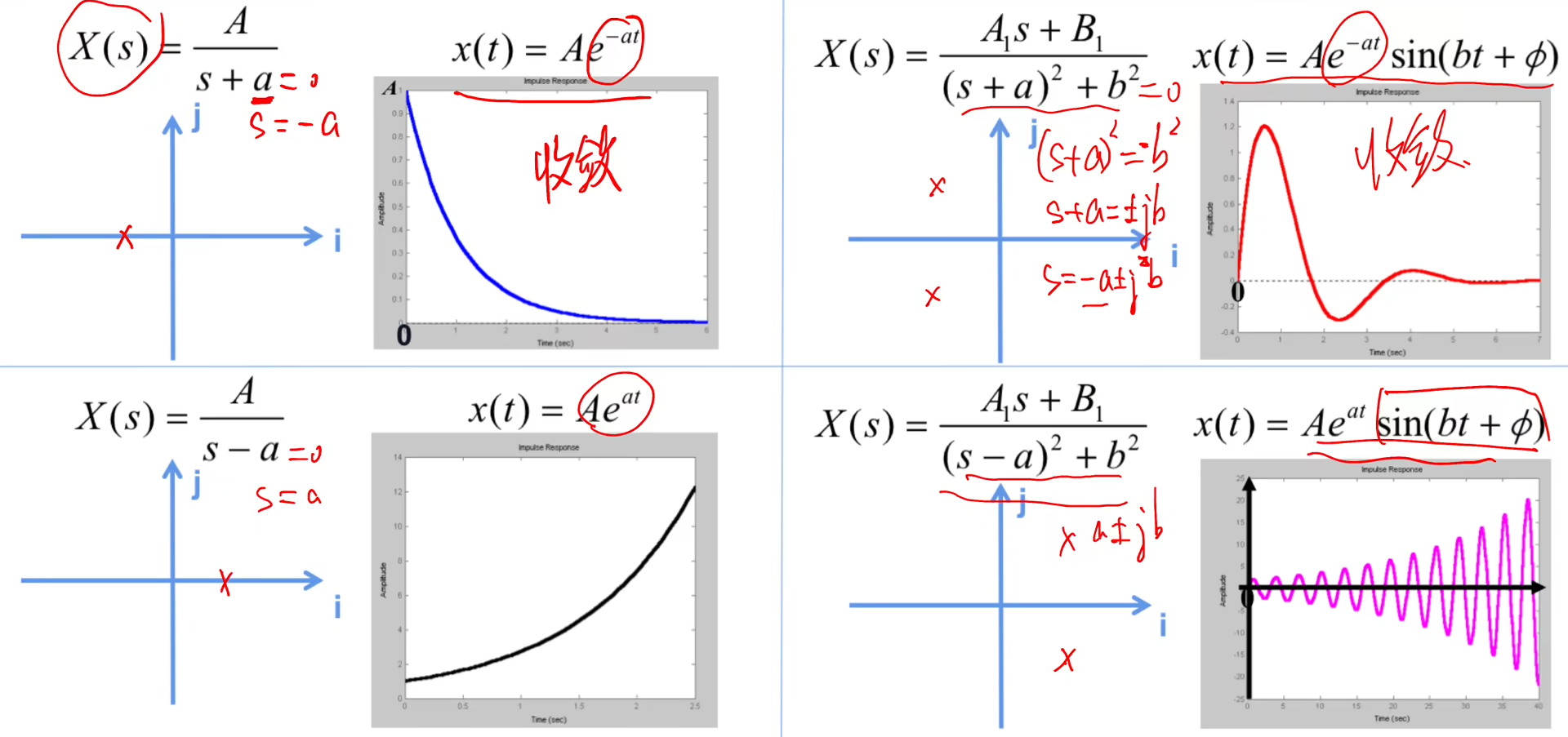
我们观察发现,
上面两幅图在t趋于无穷的时候都达到了稳态,逐渐收敛。
而下面两幅图其输出响应反而随着时间越来越大,逐渐发散了。
那么对应的极点关系是什么样的?
上面两幅图的极点都是-a,即极点在复平面的左半侧;
下面两幅图的极点都是a,即极点在复平面的右半侧。
这是必然的吗?显然是的,研究极点与模态关系时我们知道:极点-α经过反拉氏变换成为模态的λ参数,因此只要极点为负数,那么模态肯定包含这一项,必定收敛。

同上,对比左右两侧的图,可以发现,只要特征根为复数根,则必然包含/
震荡项。
规律:
也就是说,特征根的正负决定了系统的稳定性。
只要特征根为复数根,则必然包含震荡项。
以下是本节课需要达到的理解深度:
总体思路:
在输出中影响走向的项称为模态。
模态能提供系统输出响应的诸多关系,方便我们分析和设计系统。
观测系统是否收敛稳定,需要观测在时域(微分形式)内输出响应与时间的关系,因此要进行反拉氏变换。
求模态一般分为四步:
Ⅰ得到传递函数:
Ⅱ 转化为零极式:
Ⅲ 裂项或凑数对表:
Ⅳ 反拉氏变换:
任何代数方程都可以转化为零极式,零极式可以裂项或凑数对表,化简后进行反拉氏变换为三种在时域中对应的解,解就是系统的模态。
其中解中e的系数λ就是代数方程分母为零的解,即传递函数的极点α,也是特征方程的特征根。
通过构建特征根(极点)与模态的关系,我们知道任何微分方程都可以按根的情况分成三种,可以获得对应的三种模态,进而判断输出响应与时间的关系,这也是为什么任意系统都可以进行模态分析的原因。
通过构建特征根(极点)与稳定性、震荡性的关系,我们可以从复平面观测极点的分布,从而分析一个系统的稳定与否,震荡与否。
在输出响应与时间的关系图上,
模态(极点决定)和分子零点共同决定曲线的形状,但是否稳定是由模态决定的,他影响系统的走势。函数的零点并不影响系统的模态,但他们影响各模态在响应中站的比重,进而影响响应曲线的形状。
写在后面:
很开心你能耐着性子读到这里,很荣幸能将我的三脚猫知识分享给大家。
星马也是小白,因此更懂小白的心思。这篇文章也还有很多不足之处,或是纰漏,希望你发现了及时在评论区提醒我呀~
(人工智能学院就是每周四五天满课的啦,最近期中考试,更新基本随缘~)
别丢收藏夹吃灰啦好嘛~
星马是刚入门的大菜比,有错望指正,有项目可以带带我。



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








