你真的懂C语言中的取余和取模吗

进击的大俊

已于 2023-12-16 18:22:00 修改

阅读量1.1k

点赞数 15

分类专栏： C语言文章标签： c语言算法开发语言

于 2023-12-16 18:17:56 首次发布

本文链接：https://blog.csdn.net/2301_80322352/article/details/135035358

版权

C语言专栏收录该内容

11 篇文章

订阅专栏

关于“取整”你得知道

首先谈谈关于数学取整的问题

//demo 1
#include <stdio.h>
int main()
{
  //本质是向0取整
  int i = -2.9;
  int j = 2.9;
  printf("%d\n", i); //结果是：-2
  printf("%d\n", j); //结果是：2
  return 0;
}
//有一个trunc取整函数，同作用

//demo 2
#include <stdio.h>
#include <math.h> //因为使用了floor函数，需要添加该头文件
int main()
{
  //本质是向-∞取整，注意输出格式要不然看不到结果
  printf("%.1f\n", floor(-2.9)); //-3
  printf("%.1f\n", floor(-2.1)); //-3
  printf("%.1f\n", floor(2.9)); //2
  printf("%.1f\n", floor(2.1)); //2
  return 0;
}

//demo 3
#include <stdio.h>
#include <math.h>
int main()
{
  //本质是向+∞取整，注意输出格式要不然看不到结果
  printf("%.1f\n", ceil(-2.9)); //-2
  printf("%.1f\n", ceil(-2.1)); //-2
  printf("%.1f\n", ceil(2.9)); //3
  printf("%.1f\n", ceil(2.1)); //3
  return 0;
}

//demo4
#include <stdio.h>
#include <math.h>
int main()
{
//本质是四舍五入
  printf("%.1f\n", round(2.1));
  printf("%.1f\n", round(2.9));
  printf("%.1f\n", round(-2.1));
  printf("%.1f\n", round(-2.9));
  return 0;
}

汇总例子

#include <stdio.h>
#include <math.h>
int main()
{
  const char * format = "%.1f \t%.1f \t%.1f \t%.1f \t%.1f\n";
  printf("value\tround\tfloor\tceil\ttrunc\n");
  printf("-----\t-----\t-----\t----\t-----\n");
  printf(format, 2.3, round(2.3), floor(2.3), ceil(2.3), trunc(2.3));
  printf(format, 3.8, round(3.8), floor(3.8), ceil(3.8), trunc(3.8));
  printf(format, 5.5, round(5.5), floor(5.5), ceil(5.5), trunc(5.5));
  printf(format, -2.3, round(-2.3), floor(-2.3), ceil(-2.3), trunc(-2.3));
  printf(format, -3.8, round(-3.8), floor(-3.8), ceil(-3.8), trunc(-3.8));
  printf(format, -5.5, round(-5.5), floor(-5.5), ceil(-5.5), trunc(-5.5));
  return 0;
}

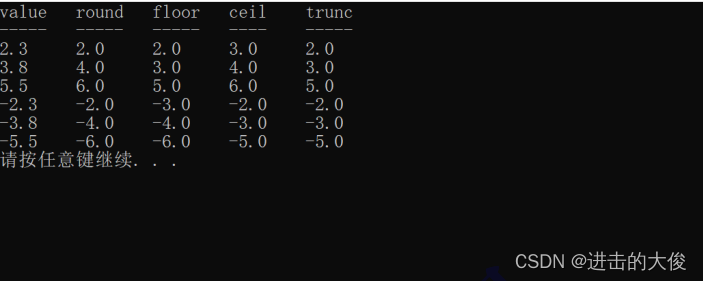
结论：浮点数（整数/整数），是有很多的取整方式的。

聊聊取模

取模概念：

如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r 且0≤r<d。其中，q 被称为商，r 被称为余数。

//对应代码
#include <stdio.h>
int main()
{
  int a = 10;
  int d = 3;
  printf("%d\n", a%d); //结果是1
  //因为：a=10,d=3,q=3,r=1 0<=r<d(3)
  //所以：a = q*d+r -> 10=3*3+1
  return 0;
}

如果是下面的代码呢?

#include <stdio.h>
int main()
{
  int a = -10;
  int d = 3;
  //printf("%d\n", a/d); //C语言中是-3，很好理解
  printf("%d\n", a%d);
  return 0;
}

gcc 4.8.5环境下

python 3.7.3环境下

备注：大家如果条件允许，可以在更多的计算器或者语言中进行测试。这里够了。

结论：很显然，上面关于取模的定义，并不能满足语言上的取模运算。

因为在C中，现在-10%3出现了负数，根据定义：满足 a = q*d + r 且0 ≤ r < d，C语言中的余数，是不满足定义的，因为，r<0了。

故，大家对取模有了一个修订版的定义：

如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r , q 为整数，且0 ≤ |r| < |d|。其中，q 被称为商，r 被称为余数。

有了这个新的定义，那么C中或者Python中的“取模”，就都能解释了。

解释C: -10 = (-3) * 3 + (-1)

解释Python：-10 = （?）* 3 + 2,其中，可以推到出来,'?'必须是-4(后面验证).即-10 = （-4）* 3 + 2，才能满足定义。

所以，在不同语言，同一个计算表达式，负数“取模”结果是不同的。我们可以称之为分别叫做正余数和负余数

是什么决定了这种现象

由上面的例子可以看出，具体余数r的大小，本质是取决于商q的。

而商，又取决谁呢？取决于除法计算的时候，取整规则。

取余和取模一样吗？

细心的大家，应该看到了，我上面的取模都是带着" "的。说明这两个并不能严格等价(虽然大部分情况差不多) 取余或者取模，都应该要算出商，然后才能得出余数。

本质 1 取整：

取余：尽可能让商，进行向0取整。

取模：尽可能让商，向-∞方向取整。

故：

C中%,本质其实是取余。

Python中%，本质其实是取模。（后面不考虑python，减少难度）

理解链：

对任何一个大于0的数，对其进行0向取整和-∞取整，取整方向是一致的。故取模等价于取余。

对任何一个小于0的数，对其进行0向取整和-∞取整，取整方向是相反的。故取模不等价于取余。

同符号数据相除，得到的商，一定是正数（正数vs正整数），即大于0！

故，在对其商进行取整的时候，取模等价于取余。

本质 2 符号：

参与取余的两个数据，如果同符号，取模等价于取余。

vs2022环境下

//计算数据同符号
#include <stdio.h>
int main()
{
   printf("%d\n", 10/3);
   printf("%d\n\n", 10 % 3);

   printf("%d\n", -10 / -3);
   printf("%d\n\n", -10 % -3);

   return 0;
}

python 3.7环境下

>>> print(10//3)

3

>>> print(10%3)

1

>>> print(-10//-3)

3

>>> print(-10%-3)

-1

题外话：注意：python中 / 默认是浮点数除法，//才是整数除法，并进行-∞取整

>>> print(10/3)

3.3333333333333335

>>> print(-10/3)

-3.3333333333333335

>>> print(10//3)

3

>>> print(-10//3)

-4

结论：通过对比试验，更加验证了，参与取余的两个数据，如果同符号，取模等价于取余

如果参与运算的数据，不同符号呢？

#include <stdio.h>
int main()
{
  printf("%d\n", -10 / 3);     //结果：-3
  printf("%d\n\n", -10 % 3);   //结果：-1   为什么? -10=(-3)*3+(-1)

  printf("%d\n", 10 / -3);     //结果：-3
  printf("%d\n\n", 10 % -3);   //结果：1    为什么？10=(-3)*(-3)+1
  return 0;
}

//明显结论：如果不同符号，余数的求法，参考之前定义。而余数符号，与被除数相同

真的吗？

python环境下

>>> print(-10//3)

-4

>>> print(10//-3)

-4

>>> print(-10%3)

2

>>> print(10%-3)

-2

wtf ，完犊子，为什么呢？

重新看看定义：

如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r , q 为整数，且0 ≤ |r| < |d|。其中，q 被称为商，r 被称为余数。

a = q*d + r 变换成 r = a - q*d 变换成 r = a + (-q*d) 对于：x = y + z，这样的表达式，x的符号与 |y|、|z|中大的数据一致。

而r = a + (-q*d)中，|a| 和 |-q*d|的绝对值谁大，取决于商q的取整方式。

c是向0取整的，也就是q本身的绝对值是减小的。

如：

-10/3=-3.333.33 向0取整 -3. a=-10 |10|, -q*d=-(-3)*3=9 |9|

10/-3=-3.333.33 向0取整 -3. a=10 |10|, -q*d=-(-3)*(-3)=-9 |9|

绝对值都变小了

python是向-∞取整的，也就是q本身的绝对值是增大的。

-10/3=-3.333.33 //向-∞取整 -4. a=-10 |10|, -q*d= -(-4)*3=12 |12|

10/-3=--3.333.33 //向-∞取整 -4. a=10 |10|, -q*d= -(-4)*(-3)=-12 |12|

绝对值都变大了

结论：如果参与取余的两个数据符号不同，在C语言中(或者其他采用向0取整的语言如：C++，Java)，余数符号，与被除数相同。

总结

1.浮点数(或者整数相除)，是有很多的取整方式的。

2.如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r , q 为整数，且0 ≤ |r| < |d|。其中，q 被称为商，r 被称为余数。

3.在不同语言，同一个计算表达式，“取模”结果是不同的。我们可以称之为分别叫做正余数和负余数。

4.具体余数r的大小，本质是取决于商q的。而商，又取决于除法计算的时候，取整规则。

5.取余vs取模：取余尽可能让商，进行向0取整。取模尽可能让商，向-∞方向取整。

6.参与取余的两个数据，如果同符号，取模等价于取余。

7.如果参与取余的两个数据符号不同，在C语言中(或者其他采用向0取整的语言如：C++，Java)，余数符号，与被除数相同。（因为采用的向0取整）

基本上关于C语言中有关取模和取余的内容已经描述完了，如果帮助到大家，麻烦点赞加关注哦！！