动态规划精进篇：当终点在“世界之外”——出界的路径数

原创于 2025-10-05 10:18:21 发布 · 1k 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #算法

动态规划专栏收录该内容

8 篇文章

订阅专栏

哈喽，各位小伙伴们，我是前端小L。

在上一篇激动人心的文章中，我们首次将“约束条件”（油量）融入DP状态，成功解决了一个抽象的图路径问题。那次经历，让我们掌握了DP思维的“升维”武器。

今天，我们将趁热打铁，带着这把锋利的武器，重返我们熟悉的“二维网格”战场。但这次的任务极其特殊：我们的目标不再是地图上的任何一个点，而是要想尽办法逃离这个世界——走出边界！这是一个看似简单，却能完美展现“DP状态设计”艺术的绝佳问题。

话不多说，直接开始~

力扣 576. 出界的路径数

https://leetcode.cn/problems/out-of-boundary-paths/

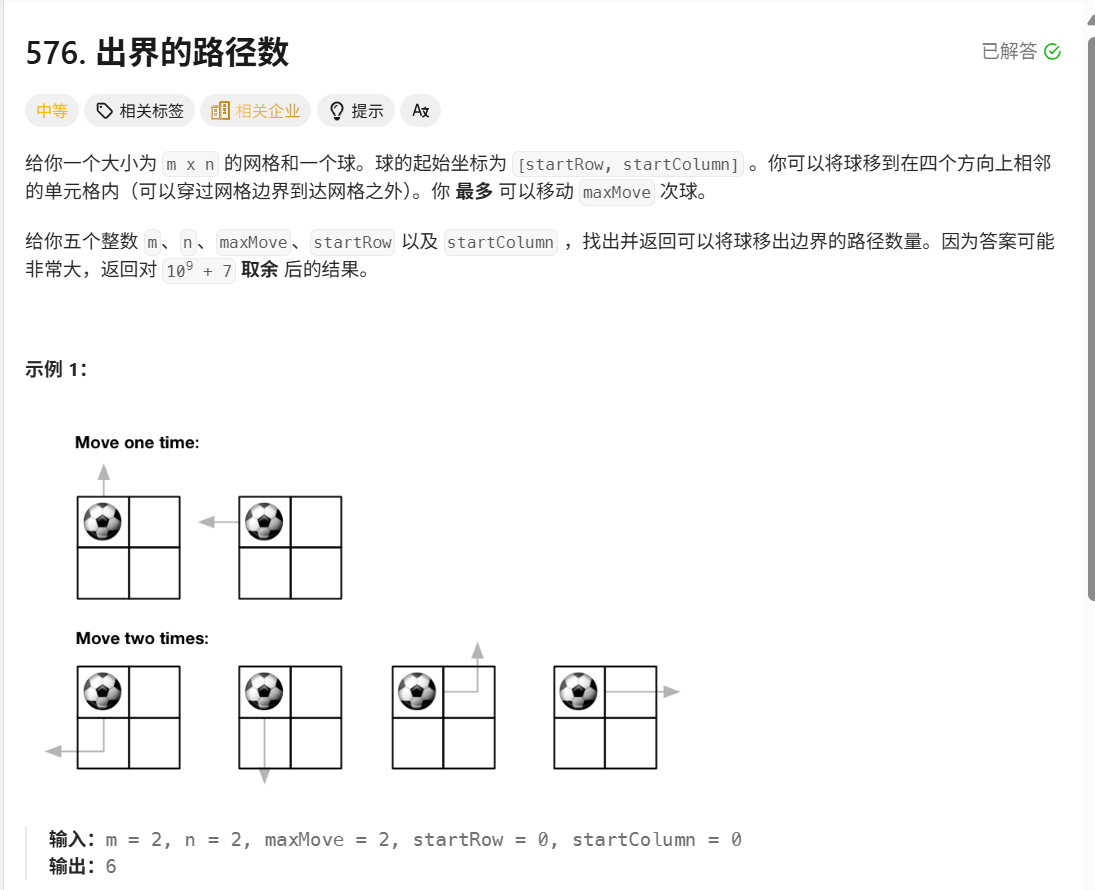
题目分析：

地图：还是老朋友 m x n 网格。
玩家：一个放在 (startRow, startColumn) 的小球。
行动力：最多可以移动 maxMove 次，每次可以向上下左右四个方向移动一格。
胜利条件：在 maxMove 步之内（或刚好用完），将小球移出网格边界。
目标：计算所有可能“出界”的路径总数，结果取模。

这个问题完美地融合了我们之前学过的知识点：它有“网格”的形态，同时又有一个类似“油量”的约束条件——“剩余步数”。这简直是为我们量身定做的练习题！

思路一：再次请出“记忆化搜索”这位老朋友 (自顶向下DP)

面对这种“从A点出发，走K步，有多少种可能”的问题，最符合直觉的永远是递归（深度优先搜索）。

1. 定义递归函数： 我们需要一个函数来回答这个核心问题：“我现在在 (i, j)，还剩 k 步，请问有多少种方法可以出界？” dfs(i, j, k)

2. 寻找递归的终点（Base Cases）：

成功终点：当我们发现当前位置 (i, j) 已经在边界之外时 (i < 0 或 i >= m 或 j < 0 或 j >= n)，说明我们已经成功“越狱”了！这是一条合法的出界路径，我们返回 1。

失败终点：如果我们步数用完了 (k == 0)，但人还在网格里，那就再也无法出界了。这是一条失败的路径，返回 0。

3. 状态转移（递归逻辑）： 如果不在终点，我们就尝试从 (i, j) 向四个方向移动。假设移动到邻居 (ni, nj)，那么问题就变成了“从 (ni, nj) 出发，还剩 k-1 步，有多少种方法可以出界？”。这不就是调用 dfs(ni, nj, k-1) 吗！所以，dfs(i, j, k) 的结果，就是它四个方向的邻居的 dfs 结果之和。

4. 记忆化“升维”： 和上一题一样，朴素的DFS会因为大量重复的 (位置, 剩余步数) 状态而超时。我们需要一个备忘录来记录算过的结果。这个状态由三个变量定义：行 i，列 j，剩余步数 k。所以，我们的DP数组必须是三维的！ dp[k][i][j]：表示从 (i, j) 出发，还剩 k 步的情况下，出界的路径总数。

代码实现 (自顶向下DP):

class Solution {
public:
    int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
        // dp[k][i][j]: 从(i,j)出发，剩k步，出界的路径数
        // 初始化为-1表示未计算
        dp.resize(maxMove + 1, vector<vector<int>>(m, vector<int>(n, -1)));
        this->m = m;
        this->n = n;
        return dfs(maxMove, startRow, startColumn);
    }

private:
    vector<vector<vector<int>>> dp;
    int m, n;
    int mod = 1e9 + 7;
    int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; // 四个方向

    int dfs(int k, int i, int j) {
        // Base Case 1: 成功出界
        if (i < 0 || i >= m || j < 0 || j >= n) {
            return 1;
        }
        // Base Case 2: 步数用尽，失败
        if (k == 0) {
            return 0;
        }
        // 记忆化：如果算过，直接返回
        if (dp[k][i][j] != -1) {
            return dp[k][i][j];
        }

        long long count = 0;
        // 状态转移：探索四个方向
        for (auto& dir : dirs) {
            count = (count + dfs(k - 1, i + dir[0], j + dir[1])) % mod;
        }

        // 写入备忘录并返回
        return dp[k][i][j] = count;
    }
};

思路二：自底向上，从“0步”构建到“K步” (迭代DP)

自顶向下的方法很直观，但自底向上的迭代法往往能带来更深的理解和更好的性能。

1. 重新定义 dp 数组含义： dp[k][i][j] 表示：通过恰好 k 步，从起点走到 (i, j) 的路径总数。

2. 初始化： 在 k=0 时，我们哪里也没去，就在起点。所以 dp[0][startRow][startColumn] = 1。其他所有 dp[0][i][j] 均为 0。

3. 状态转移方程： 要用 k 步走到 (i, j)，我们必须在 k-1 步时，位于 (i, j) 的某个邻居 (pi, pj)。所以，dp[k][i][j] 的值，等于所有邻居在 k-1 步时的路径数之和。 dp[k][i][j] = dp[k-1][i-1][j] + dp[k-1][i+1][j] + dp[k-1][i][j-1] + dp[k-1][i][j+1] (注意处理边界)

4. 如何计算最终答案？ 最终答案是所有“出界”路径的总和。一条路径在什么时候算作出界？当我们在第 k 步，位于某个边界格子 (i, j) 时，下一步就会出界。所以，我们可以在计算完每一轮 k 的 dp 表后，遍历整个网格。对于每一个格子 (i, j)，如果 dp[k][i][j] 大于0，我们就看看它往四个方向走，有多少个方向是出界的，然后把 dp[k][i][j] 累加相应次数到最终结果 ans 中。

5. 空间优化： 我们注意到，计算第 k 步的状态，只依赖于第 k-1 步。这又是我们熟悉的“滚动数组”优化信号！我们可以把三维dp[k][i][j]压缩成两个二维数组 current_dp[i][j] 和 prev_dp[i][j]。

代码实现 (自底向上DP + 空间优化):

class Solution {
public:
    int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
        int mod = 1e9 + 7;
        // dp[i][j]: 当前步数下，到达(i,j)的路径数
        vector<vector<int>> dp(m, vector<int>(n, 0));
        dp[startRow][startColumn] = 1;

        long long ans = 0;
        int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};

        // 迭代 k 从 0 到 maxMove - 1 步
        for (int k = 0; k < maxMove; ++k) {
            vector<vector<int>> temp_dp(m, vector<int>(n, 0));
            for (int i = 0; i < m; ++i) {
                for (int j = 0; j < n; ++j) {
                    // 如果当前格子在上一步可达
                    if (dp[i][j] > 0) {
                        for (auto& dir : dirs) {
                            int ni = i + dir[0];
                            int nj = j + dir[1];

                            // 如果下一步出界了
                            if (ni < 0 || ni >= m || nj < 0 || nj >= n) {
                                ans = (ans + dp[i][j]) % mod;
                            } 
                            // 如果还在界内
                            else {
                                temp_dp[ni][nj] = (temp_dp[ni][nj] + dp[i][j]) % mod;
                            }
                        }
                    }
                }
            }
            dp = temp_dp; // 更新dp表为下一步的结果
        }
        return ans;
    }
};