Linear Regression-附上全部代码（线性回归+过拟合处理）--机器学习最基础的算法

原创已于 2025-12-03 09:16:12 修改 · 476 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #线性回归 #机器学习

于 2025-12-03 04:05:48 首次发布

一、算法引言

线性回归是在已有数据集上通过构建一个线性的模型来拟合该数据集特征向量的各个分量之间的关系，对于需要预测结果的新数据，我们利用已经拟合好的线性模型来预测其结果。最小二乘法是用的比较广泛的一种方法。

二、算法解析

我们先来讨论什么是线性回归，如果说我们有一组数据，数据包含特征（X）和标签(y)，那么我们如何根据已有的数据拟合出一条直线来完美的符合已有数据，从而达到对未知数据的预测功能。这就是线性回归的作用。

然后来讨论什么是最小二乘法，高斯于 1823 年在误差独立同分布的假定下，证明了最小二乘方法的一个最优性质: 在所有无偏的线性估计类中 , 最小二乘方法是其中方差最小的！对于数据 (xi,yi)(i=1,2,3...,n)，拟合出函数 ℎ(x)有误差，即残差：ri=ℎ(xi)−yi，此时 L2 范数(残差平方和) 最小时， h(x) 和 y 相似度最高，更拟合一般的 H(x) 为 n 次的多项式： H(x)=w0+w1x+w2x2+...wnxn ，其中 w(w0,w1,w2,...,wn)为参数，最小二乘法就是要找到一组 w(w0,w1,w2,...,wn)，使得残差平方和最小。

最后来考虑最小二乘法和线性回归有什么关系，既然拟合直线，那么第一次初始化多项式参数，模型肯定是不够精确的，这时候我们就可以利于预测值与真实值之间的差距（也就是损失），利用反向传播计算梯度，使用梯度下降算法去更新参数。

这里给出根据最小二乘法引出的代价函数（这里乘上二分之一是为了计算梯度）

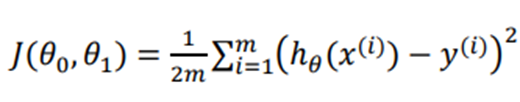
我们在这里采用梯度下降的方法最小化我们的目标函数，同样给出梯度下降得公式：

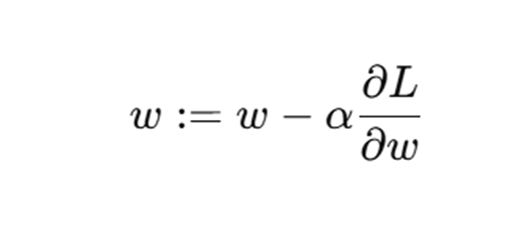
三、代码解析

随机生成目标函数y=sin2πx的离散数据：

#随机生成0-1的30个数据，并生成对应的y, 使用random里面的randn引入随机噪声
np.random.seed(0)
x = np.linspace(0, 1, 30)
y = np.sin(2 * np.pi * x) + 0.1 * np.random.randn(30)

定义多项式预测函数：

#定义多项式预测函数
def polynomial(x, w):
    y_pred = 0
    for i in range(len(w)):
        y_pred += w[i] * (x ** i)
    return y_pred

定义损失函数即目标函数，套用上面的公式：

def loss(x, y, w):
    total = 0
    for i in range(len(x)):
        y_pred = polynomial(x[i], w)
        total += (y_pred - y[i]) ** 2
    return total / (2 * len(x))

采用梯度下降的方法最小化我们的目标函数，套用上面的公式：

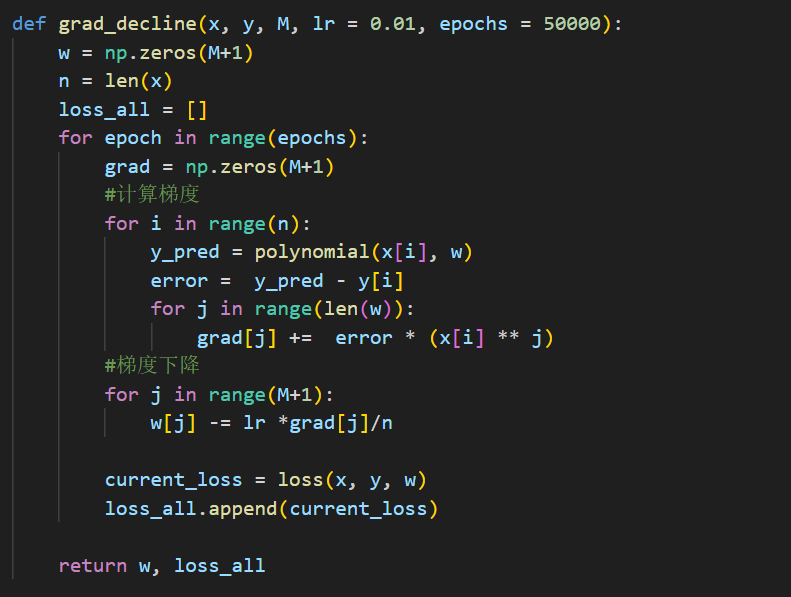
与此同时这里也进行损失计算，返回损失值

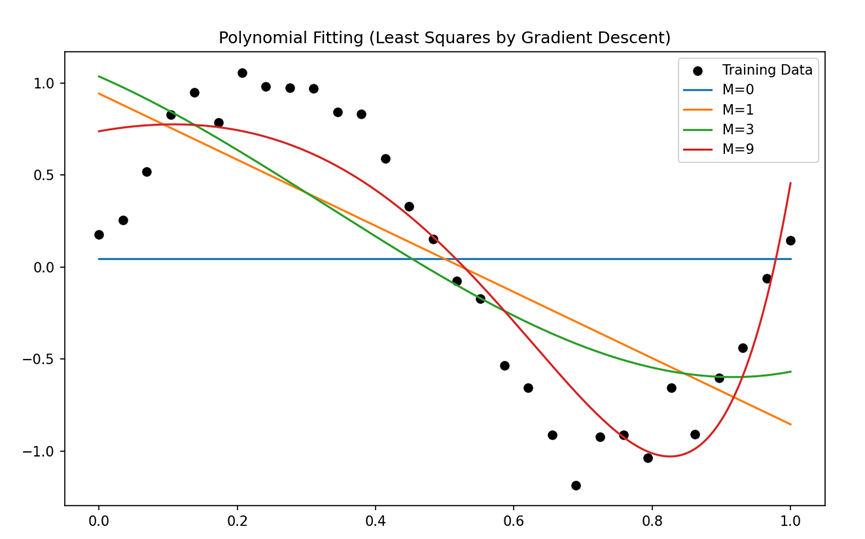
绘制拟合曲线：

输出结果：

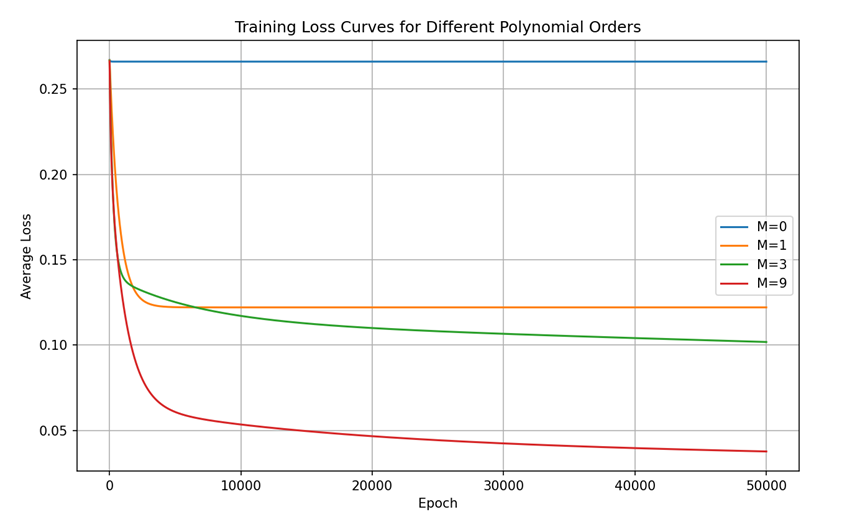
绘制训练损失曲线：

输出结果：

四、手写代码反馈结果

通过这次手写代码，让我知道了以下几个点：

在计算梯度时，对于每个变量的损失公式为error = y_pred - y[i]

若使用这个error = y[i] - y_pred，则会带来出现以下警告：

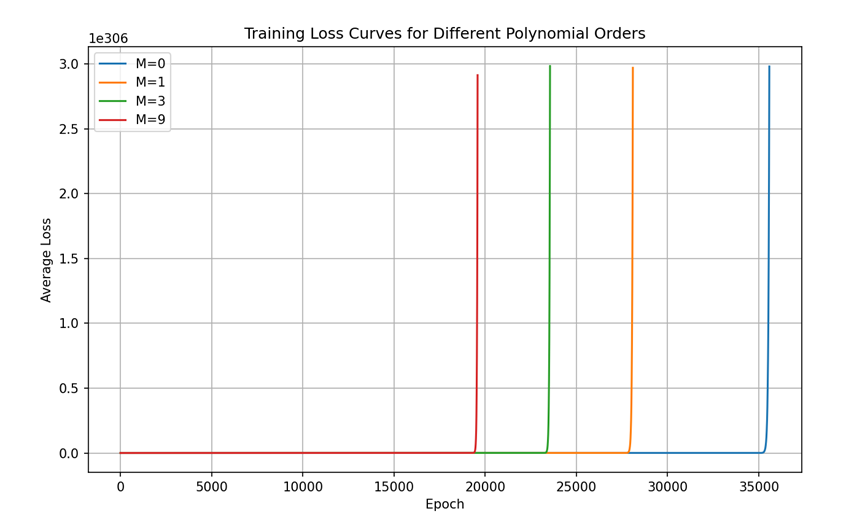
这些警告表明在计算过程中出现了数值溢出问题，拟合的曲线，也明显不正确。

给出拟合直线的运行图

给出损失-训练轮次的结果

五、引出过拟合

这里我们可以先讨论一下，什么是过拟合，下面给出我对过拟合的理解，

过拟合是指模型虽然能非常好地适应我们的训练集，但在新输入变量进行预测时可能会效果不好。

然后来讨论为什么会出现过拟合的情况，就以多项式理解，x的次数越高，拟合的效果越好，但相应的预测的能力就可能变差。

最后来讨论如何解决过拟合的情况

1.丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如 PCA）

2.正则化。保留所有的特征，但是减少参数的大小（magnitude）。

很显然，我们这里使用正则化线性回归，这里给出正则化线性回归的代价函数：

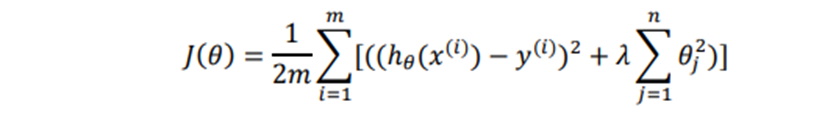
然后来理解为什么增加的这一项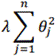可以让参数值变小，因为如果我们令正则化参数的值很大的话，为了使代价函数尽可能的小，所有的参数值（不包括j=0）都会在一定程度上减小。

同样的，我们使用梯度下降算法使得这个代价函数最小化

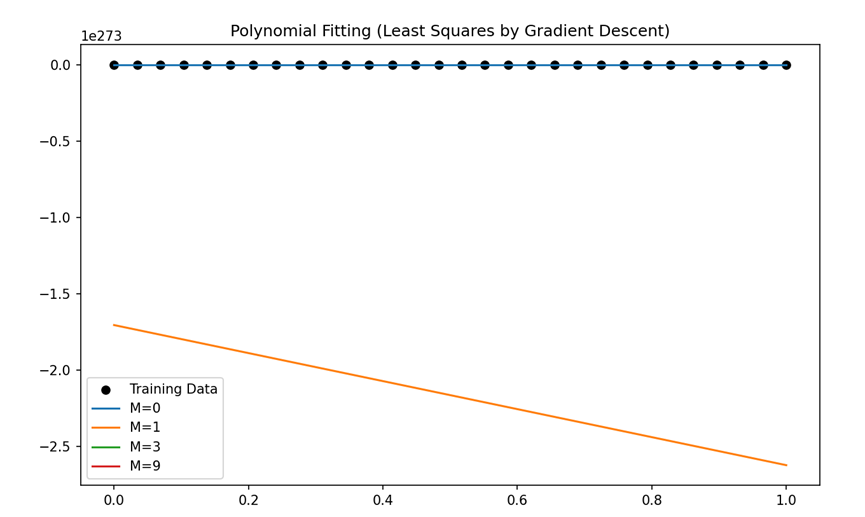
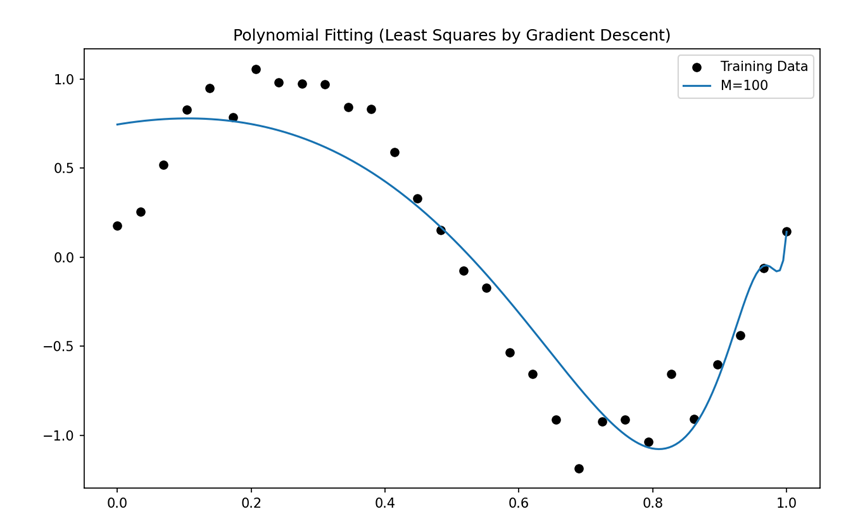
由于模型太简单，我写的代码九阶不足以体现过拟合，因此我这里使用100阶来进行展示。

这个是正则化前的：

拟合曲线：

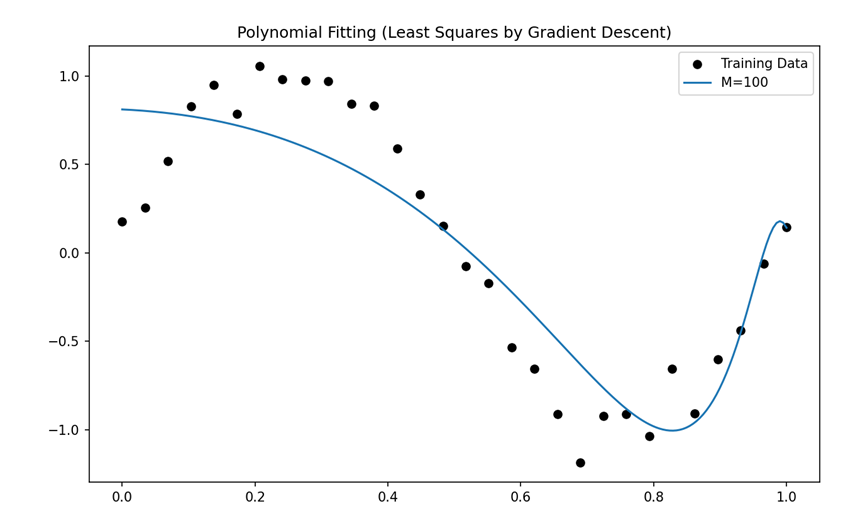
那么我们就要处理过拟合，这里对过拟合采用正则化的手段

我们先来看处理完过拟合后的运行效果

拟合直线的运行截图

给出损失-训练轮次的结果

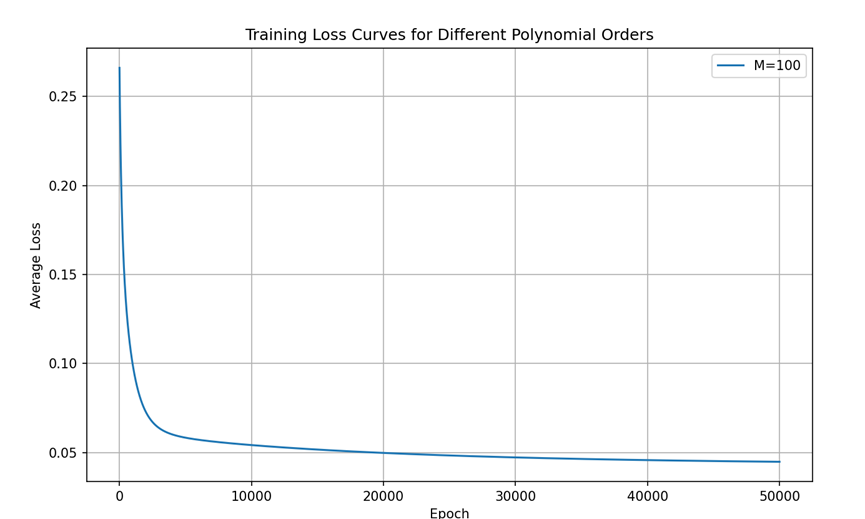
这里看出效果很好！！

可以看出模型效果相对于100阶的拟合曲线变好了很多，但是发现损失值增大了，不过这个对比没有意义，因为损失值本身不能直接与未正则化的损失值比较，需要理解它衡量的是拟合误差 + 权重惩罚。

六、线性回归+最小二乘法完整代码（未进行正则化）

import numpy as np
import matplotlib.pyplot as plt

#随机生成0-1的30个数据，并生成对应的y, 使用random里面的randn引入随机噪声
np.random.seed(0)
x = np.linspace(0, 1, 30)
y = np.sin(2 * np.pi * x) + 0.1 * np.random.randn(30)


#定义多项式预测函数
def polynomial(x, w):
    y_pred = 0
    for i in range(len(w)):
        y_pred += w[i] * (x ** i)
    return y_pred
    

def loss(x, y, w):
    total = 0
    for i in range(len(x)):
        y_pred = polynomial(x[i], w)
        total += (y_pred - y[i]) ** 2
    return total / (2 * len(x))
    
def grad_decline(x, y, M, lr = 0.01, epochs = 50000):
    w = np.zeros(M+1)
    n = len(x)
    loss_all = []
    for epoch in range(epochs):
        grad = np.zeros(M+1)
        #计算梯度
        for i in range(n):
            y_pred = polynomial(x[i], w)
            error =  y_pred - y[i]
            for j in range(len(w)):
                grad[j] +=  error * (x[i] ** j)
        #梯度下降
        for j in range(M+1):
            w[j] -= lr *grad[j]/n
            
        current_loss = loss(x, y, w)
        loss_all.append(current_loss)
        
    return w, loss_all


def plot_fit(x, y, Ms, lr=0.01, epochs=50000):
    plt.figure(figsize=(10,6))
    plt.scatter(x, y, color='black', label="Training Data")

    for M in Ms:
        w, _ = grad_decline(x, y, M, lr, epochs)
        X_plot = np.linspace(0, 1, 200)
        Y_plot = np.array([polynomial(xv, w) for xv in X_plot])
        plt.plot(X_plot, Y_plot, label=f"M={M}")

    plt.legend()
    plt.title("Polynomial Fitting (Least Squares by Gradient Descent)")
    plt.show()


def plot_loss_curve(x, y, Ms, lr=0.01, epochs=50000):
    plt.figure(figsize=(10,6))
    for M in Ms:
        _, loss_history = grad_decline(x, y, M, lr, epochs)
        plt.plot(range(1, epochs+1), loss_history, label=f"M={M}")

    plt.xlabel("Epoch")
    plt.ylabel("Average Loss")
    plt.title("Training Loss Curves for Different Polynomial Orders")
    plt.legend()
    plt.grid(True)
    plt.show()

# 主流程
# Ms = [0, 1, 3, 100]
Ms = [100]
plot_fit(x, y, Ms, lr=0.01, epochs=50000)
plot_loss_curve(x, y, Ms, lr=0.01, epochs=50000)

七、线性回归+最小二乘法完整代码（进行正则化）

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)
x = np.linspace(0, 1, 30)
y = np.sin(2 * np.pi * x) + 0.1 * np.random.randn(30)

def polynomial(x, w):
    y_pred = 0
    total = 0
    for i in range(len(w)):
        y_pred = w[i] * (x ** i)
        total += y_pred
    return total

def loss(x, y, w, lam = 0.0):
    total = 0
    for i in range(len(x)):
        y_pred =  polynomial(x[i], w)
        total += (y_pred - y[i]) ** 2
    total = total / (2 * len(x) )
    total += lam * np.sum(np.array(w) **2)
    return total

def grad_decline(x, y, W, lr=0.01, epochs=50000, lam = 0.0):
    w = np.zeros(W+1)
    n = len(x)
    loss_total =[]
    for epoch in range(epochs):
        grad = np.zeros(W+1)
        for i in range(n):
            y_pred = polynomial(x[i], w)
            error = y_pred - y[i]
            for j in range(len(w)):
                grad[j] += error * (x[i] ** j)
        
        
        for k in range(W + 1):
            grad[k] += 2 * lam * w[k]
        
        for j in range(len(w)):
            w[j] -= (grad[j] * lr) / n
            
        loss_1 = loss(x, y, w)
        loss_total.append(loss_1)
    return w, loss_total

def plot_fit(x, y, Ms, lr=0.01, epochs=50000,lam = 0.0):
    plt.figure(figsize=(10,6))
    plt.scatter(x, y, color='black', label="Training Data")

    for M in Ms:
        w, _ = grad_decline(x, y, M, lr, epochs, lam)
        X_plot = np.linspace(0, 1, 200)
        Y_plot = np.array([polynomial(xv, w) for xv in X_plot])
        plt.plot(X_plot, Y_plot, label=f"M={M}")

    plt.legend()
    plt.title("Polynomial Fitting (Least Squares by Gradient Descent)")
    plt.show()


def plot_loss_curve(x, y, Ms, lr=0.01, epochs=50000, lam = 0.0):
    plt.figure(figsize=(10,6))
    for M in Ms:
        _, loss_history = grad_decline(x, y, M, lr, epochs, lam)
        plt.plot(range(1, epochs+1), loss_history, label=f"M={M}")

    plt.xlabel("Epoch")
    plt.ylabel("Average Loss")
    plt.title("Training Loss Curves for Different Polynomial Orders")
    plt.legend()
    plt.grid(True)
    plt.show()
    
lambda_reg = 0.05  # L2 正则化系数，可调整大小    
Ms = [100]
plot_fit(x, y, Ms, lr=0.01, epochs=50000, lam=lambda_reg)

# 训练损失曲线
plot_loss_curve(x, y, Ms, lr=0.01, epochs=50000, lam=lambda_reg)