KNN从原理到实战（K - 近邻算法）--手动实现+附上全部代码

原创已于 2025-12-04 14:41:49 修改 · 167 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#近邻算法 #算法 #机器学习

于 2025-12-04 14:37:49 首次发布

一、算法引言

k 近邻法是基本且简单的分类与回归方法。k 近邻法的基本做法是：对给定的训练实例点和输入实例点，首先确定输入实例点的 k 个最近邻训练实例点，然后利用这 k 个训练实例点的类的多数来预测输入实例点的类。

k 近邻模型对应于基于训练数据集对特征空间的一个划分。k 近邻法中，当训练集、距离度量、k 值及分类决策规则确定后，其结果唯一确定。

k 近邻法三要素：距离度量、k 值的选择和分类决策规则。常用的距离度量是欧氏距离及更一般的 pL 距离。k 值小时，k 近邻模型更复杂；k 值大时，k 近邻模型更简单。 k 值的选择反映了对近似误差与估计误差之间的权衡，通常由交叉验证选择最优的 k。

常用的分类决策规则是多数表决，对应于经验风险最小化。

二、算法解析

在做这个之前，我们应该知道k近邻学习有一个明显的不足之处，他似乎没有显式的训练过程！事实上，他是“懒惰学习”的著名代表。此类学习技术在训练阶段仅仅是把样本保存起来，训练时间开销为零，待收到测试样本后再进行处理；相应的对于很多卷积神经网络以及实验一的线性回归模型，这些在训练阶段就对样本进行学习处理的方法，称为“急切学习”。

现在，让我们从代码角度去理解“懒惰学习”。

三、代码解析

以下附上代码过程

首先导入库

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

定义距离计算函数，这里使用欧氏距离：

def euclidean_distance(x1, x2):
    return np.sqrt(np.sum((x1 - x2) ** 2))

接下来让我们来定义KNN模型（手动实现）

class KNN:
    def __init__(self, k=3):
        self.k = k
    def fit(self, x, y):   #这里只是利用懒惰学习，定义变量存储数据，并非显示训练
        self.x_train = x
        self.y_train = y
    def predict_one(self, x):  #定义单个样本的预测
        dis = [euclidean_distance(x_1, x) for x_1 in self.x_train]   
        idx = np.argsort(dis)[:self.k]
        y =self.y_train[idx]  
        v, count = np.unique(y, return_counts=True)   #拿到不同类别对应的键值对，键是类别，count该类是出现的次数
        return v[np.argmax(count)]
    def predict(self, X):    #定义多个样本的预测
        return np.array([self.predict_one(x) for x in X])

加载数据集

iris = datasets.load_iris()

x = iris.data
y = iris.target

导入数据集划分库，经过我的发现，依据类别进行划分数据集，对模型的性能有较大的提升，因此我们这里导入train_test_split

from sklearn.model_selection import train_test_split
X_train2, X_test2, y_train2, y_test2 = train_test_split(
    x, y, test_size=0.3, random_state=42, stratify=y
)

实例化模型

knn = KNN(k=5)

然后调用模型，也就是调用fit函数进行模型的懒惰训练

knn.fit(X_train2, y_train2)

然后对模型开始预测

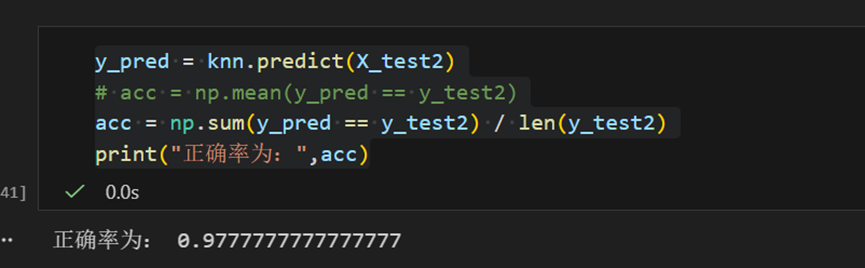
正确率还是可以的！！！

四、附上全部代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

def euclidean_distance(x1, x2):
    return np.sqrt(np.sum((x1 - x2) ** 2))

class KNN:
    def __init__(self, k=3):
        self.k = k
    def fit(self, x, y):   #这里只是利用懒惰学习，定义变量存储数据，并非显示训练
        self.x_train = x
        self.y_train = y
    def predict_one(self, x):  #定义单个样本的预测
        dis = [euclidean_distance(x_1, x) for x_1 in self.x_train]   
        idx = np.argsort(dis)[:self.k]
        y =self.y_train[idx]  
        v, count = np.unique(y, return_counts=True)   #拿到不同类别对应的键值对，键是类别，count该类是出现的次数
        return v[np.argmax(count)]
    def predict(self, X):    #定义多个样本的预测
        return np.array([self.predict_one(x) for x in X])
iris = datasets.load_iris()

x = iris.data
y = iris.target

from sklearn.model_selection import train_test_split
X_train2, X_test2, y_train2, y_test2 = train_test_split(
    x, y, test_size=0.3, random_state=42, stratify=y
)
knn = KNN(k=5)
knn.fit(X_train2, y_train2)
y_pred = knn.predict(X_test2)
# acc = np.mean(y_pred == y_test2)
acc = np.sum(y_pred == y_test2) / len(y_test2)
print("正确率为：",acc)