唯一分解定理（算术基本定理）

唯一分解定理是指：对于每一个大于1的正整数N都可以分解为有限个质数相乘且分解的形式是唯一的。

对于唯一分解定理的代码实现：

从小到大枚举（从2开始枚举，因为1可以整除任何数） 如果所枚举的数字是该数的因子那么一直整除该数 直至该数被整除为1或者该数不是所枚举数的因子则结束

不需要枚举质数，只用从小到大直接枚举即可 ，因为按照上述策略不会出现合数相乘的情况

因为合数都会被进一步分解为质数。

def f(n):

    factor=[]

    for i in range (2,n+1):

        ##如果i为n的因子，那么n一直整除i直至为1或者不为该数的因子        

        ##此处如果i从1开始那么将陷入while死循环

        while n%i==0:

            n=n//i

            factor.append(i)

        if n==1:

            break

    return factor

唯一分解定理的应用：

求正整数N的因子个数（此处可以理解为N分解为的所有质因子经过排列组合出的所有可能即为正整数N的因子）

对于代码实现N的因子之和需要用到等比求和公式

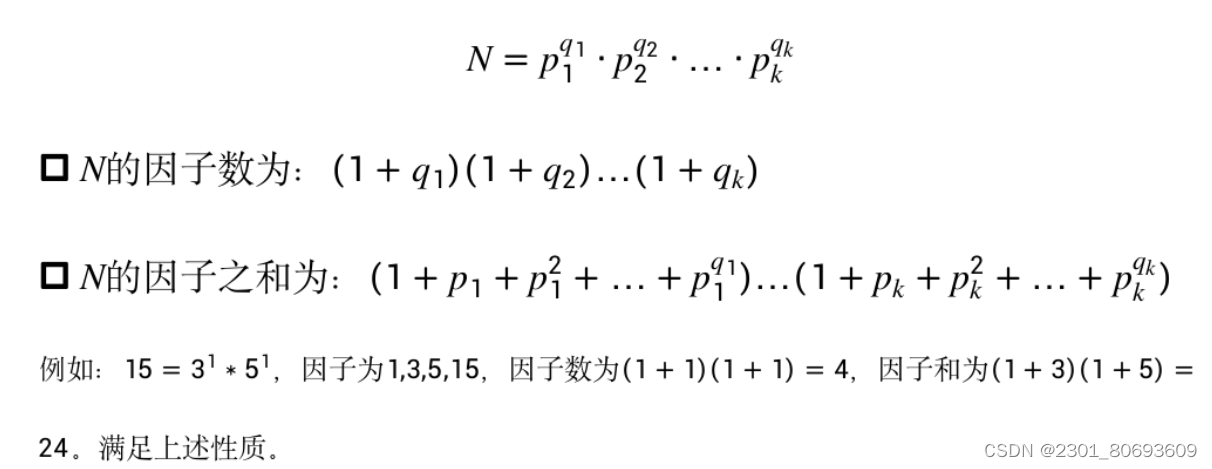
例题：求100的阶乘的正约数的个数

解题思路：

对于大于1的正整数N

它的因子个数可以通过唯一分解定理的应用来完成求解

求100的阶乘的因子个数即可以分解为求1,2,3,....100的因子个数

因为这些数为合数也是100的阶乘的因子

这些因子在唯一分解定理中可以求出各自的唯一分解定理形式

合起来即为100的阶乘的唯一分解定理形式

通过collections库中的Counter函数记录每个质因数出现的次数

（Counter(ls)可以把组合数据类型转化为计数字典）

from collections import Counter

def f(n):

    factor=[]

    for i in range (2,n+1):

        while n%i==0:

            factor.append(i)

            n//=i

        if n==1:

            break

    return factor

ls=[]

for i in range (2,101):

    ls+=f(i)

ls=Counter(ls)

ans=1

for x,y in ls.items():

    ans*=(1+y)

print(ans)