预测控制类——灰色模型预测算法

Yyyyyy&

已于 2024-08-31 22:16:36 修改

阅读量1.3k

点赞数 21

文章标签：人工智能算法 matlab 数学建模

于 2024-08-31 22:13:41 首次发布

本文链接：https://blog.csdn.net/2301_80693609/article/details/141507318

版权

本文介绍灰色模型预测算法，通过基本概念，算法原理，代码实现三部分进行讲解。

1. 灰色系统

灰色系统是由华中科技大学的邓聚龙教授80年代初所创立，在短短的三十年里已得到了长足的发展。

黑色系统：信息完全未确定的系统。

白色系统：信息完全确定的系统。

灰色系统：既有已知信息又含有未知信息的系统。

2. 灰生成技术

灰色序列生成：是一种通过对原始数据的挖掘，整理来寻求数据变化的实现规律的路径，简称灰生成。

在保持原始序列形式的前提下，改变序列中数据的值与性质。一切灰色序列都能通过某种生成弱化其随机性，显现其规律性。

常用的四种灰生成算子

1.累加生成算子（AGO）

2.逆累加生成算子（IAGO）

3.均值生成算子（MEAN）

4.级比生成算子

2.1 累加生成算子（AGO）

原始序列： $X^{^{(0)}}=(x^{^{(0)}}(1),x^{^{(0)}}(2),x^{^{(0)}}(3),...x^{^{(0)}}(n))$

生成序列： $X^{^{(1)}}=AGO(X^{(0)})=$ $(x^{(0)}(1),x^{(0)}(1)+x^{(0)}(2),...,x^{(0)}(1)+x^{(0)}(2)+...+x^{(0)}(n))$

生成序列相当于原始序列的前缀和序列

$X^{(1)}(k)=\sum_{m=1}^{k}X^{(0)}(m),(k=1,2,3,...,n)$

例子：

$X^{(0)}=(1,2,1.5,3)$

$X^{(1)}=(1,3,4.5,7.5)$

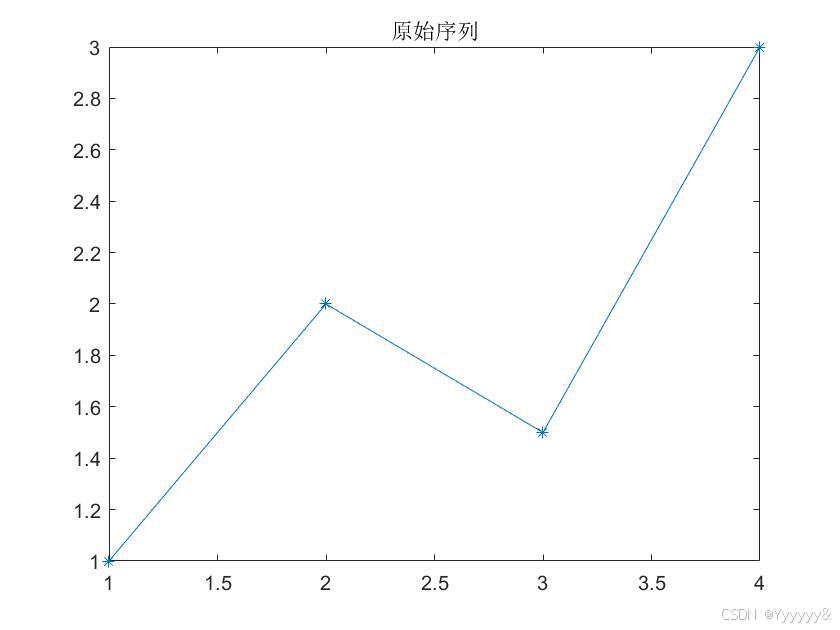
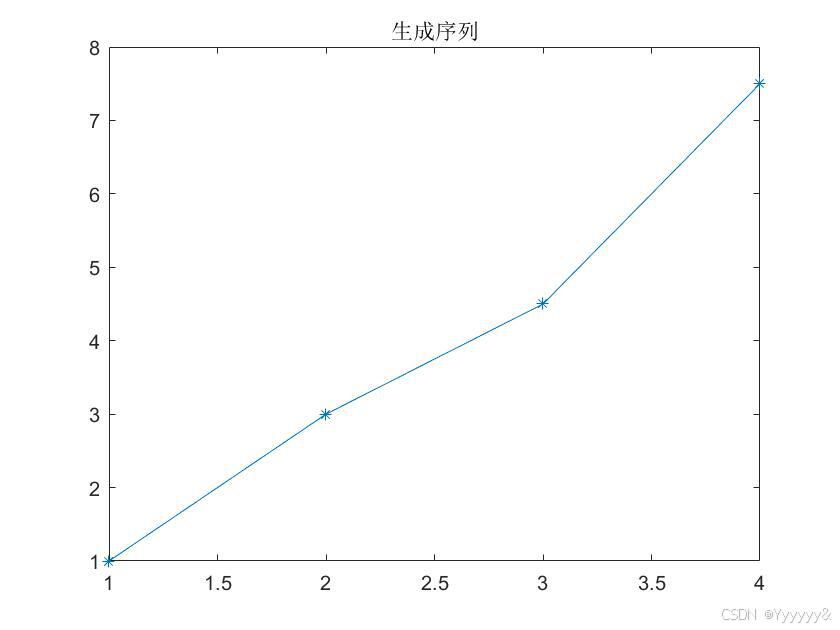
相比原始序列，经过累加算子的生成序列更能显现出规律性。

上面四个原始序列经过累加算子所得的生成序列，相比原始序列的规律性均增加。

2.2 逆累加生成算子（IAGO）

IAGO是对AGO生成序列中相邻两数依次累减，又称累减生成。

$X^{(1)}=(X^{(1)}(1),X^{(1)}(2),X^{(1)}(3),...,X^{(1)}(n))$

$Y=IAGO(X^{(1)})$

$y(k)=x^{(1)}(k)-x^{(1)}(k-1),(k>1)$

$y(1)=x(1)$

$AGO(X^{(0)})=X^{(1)}=(1,3,4.5,7.5)$

$Y=IAGOX^{(1)}=(1,2,1.5,3)$

$IAGOX^{(1)}=IAGO(AGO(X^{(0)}))=X^{(0)}$

逆累加生成算子是累加生成算子的逆运算

2.3 均值生成算子（MEAN）

均值生成算子是对AGO生成序列中相邻两数取平均值。

$z^{(1)}(k)=\frac{1}{2} (x^{(1)}(k)+x^{(1)}(k-1))$

$X^{(1)}=(1,3,4.5,7.5)$

$Z^{(1)}=(1,2,3.75,6)$

2.4 级比生成算子

级比生成序列是原始序列的前一个元素与后一个元素的比值所生成的序列。

设序列 $X^{^{(0)}}=(x^{^{(0)}}(1),x^{^{(0)}}(2),x^{^{(0)}}(3),...x^{^{(0)}}(n))$

$\sigma (k)=\frac{x^{(0)}(k-1)}{x^{(0)}(k)},k=2,3,...,n$

级比生成算子的主要作用是用来检验序列能否建立灰色预测模型所使用的。

检验准则 :

设原始序列 $X^{^{(0)}}=(x^{^{(0)}}(1),x^{^{(0)}}(2),x^{^{(0)}}(3),...x^{^{(0)}}(n))$ 的级比生成序列满足 $\sigma (k)\in (e^{-\frac{2}{n+1}},e^{\frac{2}{n+1}})$ 时，则累加生成序列 $X^{(1)}$ 可做灰色建模（GM(1,1)）。

$X^{(0)}=(1,2,1.5,3)$

$\sigma =(0.500,1.333,0.500)$

$\sigma (k)\in (e^{-\frac{2}{4+1}},e^{\frac{2}{4+1}})=(0.6703,1.4918)$

上述原始序列的级比生成序列值均在范围之内所以可以对累加生成序列建立灰色模型。

灰色理论认为系统的行为现象尽管是朦胧的，数据是复杂的，但他毕竟是有序的，是有整体功能的。灰数的生成，就是从杂乱中寻找规律。同时，灰色理论建立的是生成数据模型，不是原始数据模型。

GM(1,1)模型中G为Grey：灰色，M为Model：模型，(1,1)中的第一个1为一阶方程，第二个1为一个变量。如果预测模型有多个变量可以用回归分析等预测模型来建模。

原始序列： $X^{^{(0)}}=(x^{^{(0)}}(1),x^{^{(0)}}(2),x^{^{(0)}}(3),...x^{^{(0)}}(n))$

均值生成序列： $Z^{(1)}=(z^{(1)},z^{(2)},z^{(3)},...z^{(n)})$

称 $x^{(0)}(k)+az^{(1)}(k)=b,k=2,3,4,...,n$ 为GM(1,1)的基本形式。

把k=2,3,4...n,以及原始序列，均值生成序列带入为多项式，化为矩阵表示形式，计算出参数a，b。

$X=BP$ ,参数(a,b)的最小二乘估计为：

建立GM(1,1)的白化模型：在灰色系统中，白化是指让系统的白度增加，信息更加透明，定量关系更加明确。(离散回归连续)

$x^{(0)}(k)+az^{(1)}(k)=b$ 利用导数与微分的知识推导出 $\frac{\mathrm{d} x^{(1)}}{\mathrm{d} k}+ax^{(1)}=b$ ,利用微积分的知识求解：，由于最终是进行离散序列的预测，因此再将连续的模型离散化，

利用模型进行预测

注意：

模型检验，这里介绍相对残差检验：
残差： $q(k)=x^{(0)}(k)-\hat{x}^{(0)}(k)$

相对残差： $\varepsilon (k)=\frac{q(k)}{x^{(0)}(k)}=q(k)=\frac{x^{(0)}(k)-\hat{x}^{(0)}(k)}{x^{(0)}(k)}$

平均相对残差： $\varepsilon (avg)=\frac{1}{n}\sum_{k=1}^{n}\left | \varepsilon (k) \right |$

误差：与测量有关，衡量测量的准确性，误差越大表示测量越不准确。

残差：与预测有关，衡量预测的准确性，残差越大表示预测越不准确。

建立灰色模型的一般步骤：
1. 级比检验，建模可行性分析

2.用GM(1,1)建模

3.用模型检验

例题：

某城市1986年-1992年交通噪声数据：

代码：

clc;clear;close all
A=[71.1,72.4,72.4,72.1,71.4,72.0,71.6];
num_pred = 3;
% 级比检测
lb = exp(-2/(length(A)+1));
ub = exp(2/(length(A)+1));
for i = 1:length(A)-1
if(A(i)/A(i+1) < lb & A(i)/A(i+1) > ub)
flag = 0;
break;
end
end
if(flag == 0)
disp("级比检验不通过")
else
disp("级比检验通过,可进行灰色建模")
%建立GM(1,1)模型
syms a b;
c=[a b]';
B=cumsum(A); % 原始数据累加
n=length(A);
for i=1:(n-1)
C(i)=(B(i)+B(i+1))/2; % 生成累加矩阵
end
% 计算待定参数的值
D=A;D(1)=[];
D=D';
E=[-C;ones(1,n-1)];
c=inv(E*E')*E*D;
c=c';
a=c(1);b=c(2);
% 预测后续数据
F=[];F(1)=A(1);
for i=2:(n+num_pred)
F(i)=(A(1)-b/a)/exp(a*(i-1))+b/a ;
end
G=[];
G(1)=A(1);
for i=2:(n+num_pred)
G(i)=F(i)-F(i-1); %得到预测出来的数据
end
disp("预测结果为：" + num2str(G))
disp("平均相对残差为：")
sum(abs((G(1:length(A))-A)./A))
disp("模型精度为：")
1-sum(abs((G(1:length(A))-A)./A))