【C++数据结构】用栈实现任意进制的转换（任意进制转任意进制）（类模板）

目录

前言：

一、进制相关概念及转换方法

1.相关概念

2.输入非十进制数 

3.转为任意进制

二、代码实现

1.创建结点

2.创建栈

（1）入栈函数                

（2）出栈函数

（3）清空函数

3.定义进制转换函数

（1）创建string及int类型对象

（2）判断输入的是否为十进制数

（3）将十进制转为任意进制

（4）出栈完成转换

（5）封装成函数

（6）main函数

三、完整代码

---

前言：

        栈实现的是一种后进先出（last-in，first-out，LIFO）策略，在进制转换中将十进制数转换为n进制便是"除n取余，逆序排列"，其中我们又看到了经典的逆序，这当然是栈最擅长的，而要转换的数若非十进制则先将其转换为十进制再进行前面的操作。

---

提示：以下是本篇文章正文内容， 全是干货

一、进制相关概念及转换方法

1.相关概念

       数制：也称为计数制，是一种计数的方法，是用一组固定的符号和统一的规则来表示数值的方法。在计数过程中采用进位的方法称为进位计数制（进制），包括数位、基数和位权三个要素。

• 数位：指数字符号在一个数中所处的位置。

• 基数：指在某种进位计数制中数位上所能使用的数字符号的个数。例如十进制的基数为10。

• 位权：数制中某一位上的1所表示数值的大小（所处位置的价值）。例如十进制的230，1的位权是100，2的位权是10，3的位权是1。

2.输入非十进制数 

        若输入的为非十进制数则先将其转为十进制数，具体做法为：将每位对应的数字乘以位权再求和，下面分别以二进制数及八进制数为例：

        二进制：1101    ->    1*2^3+1*2^2+0+1=13

        八进制：0241    ->    2*8^2+4*8^1+1=161   

3.转为任意进制

方法："除n取余，逆序排列"

1.除以基数记录商和余数，如果商为0，则转换结束。

2.重复步骤，将商再次除以16，记录新的商和余数。

3.倒序排列余数，将所有步骤中得到的余数倒序排列。

4.处理特殊余数。如果余数是10到15，则在十六进制中用字母A到F表示。

        其中倒着写部分可以由栈来实现。具体操作便是将余数逐个放入栈中，然后依次出栈便完成操作，下面以将十进制数7692转换为十六进制数为例：

（1）7692除以16，商480，余数12（在十六进制中表示为C）。

（2）480除以16，商30，余数0（在十六进制中表示为30）。

（3）30除以16，商1，余数14（在十六进制中表示为E）。

（4）1除以16，商0，余数1（在十六进制中表示为1）。

（5）因此，7692的十六进制表示为1EOC。      

二、代码实现

1.创建结点

         关于结点的建立就不赘述了，这里要注意的是后面要用到的类模板Stack要先提前声明，否则在Node类里声明友元时会报错。

template<class T>class Stack;	//向前声明
template<class T>
class Node {
private:
	T m_data;	//数据域
	Node* m_next;	//指针域
public:
	Node(const T& val) {
		this->m_data = val;
	}	//有参构造
	Node& operator=(const Node& rhs) = delete;	//禁止赋值
	friend class Stack<T>;	//声明友元
};

2.创建栈

         入栈出栈清空都是基本的写法，不多赘述。

template<class T>
class Stack {
private:
	Node<T>* m_top = nullptr;	//栈顶指针
public:
	Stack() = default;	//默认构造
	Stack(const Stack&) = delete;	//禁止复制
	Stack& operator=(const Stack&) = delete;	//禁止赋值
	~Stack() {
		clear();
	};	//析构
	void clear();	//清空栈
	void push(const T& val);	//入栈
	void pop();//出栈
	bool empty()const {
		return this->m_top == nullptr;
	}	//判断是否为空
	const T& top() {
		return this->m_top->m_data;
	}	//取出栈顶元素
};

（1）入栈函数                

template<class T>
void Stack<T>::push(const T& val) {
	Node<T>* node = new Node<T>(val);
	node->m_next = this->m_top;
	this->m_top = node;
}

（2）出栈函数

template<class T>
void Stack<T>::push(const T& val) {
	Node<T>* node = new Node<T>(val);
	node->m_next = this->m_top;
	this->m_top = node;
}

（3）清空函数

template<class T>
void Stack<T>::pop() {
	if (empty()) {
		return;
	}
	Node<T>* p = this->m_top;
	this->m_top = this->m_top->m_next;
	delete p;
}

3.定义进制转换函数

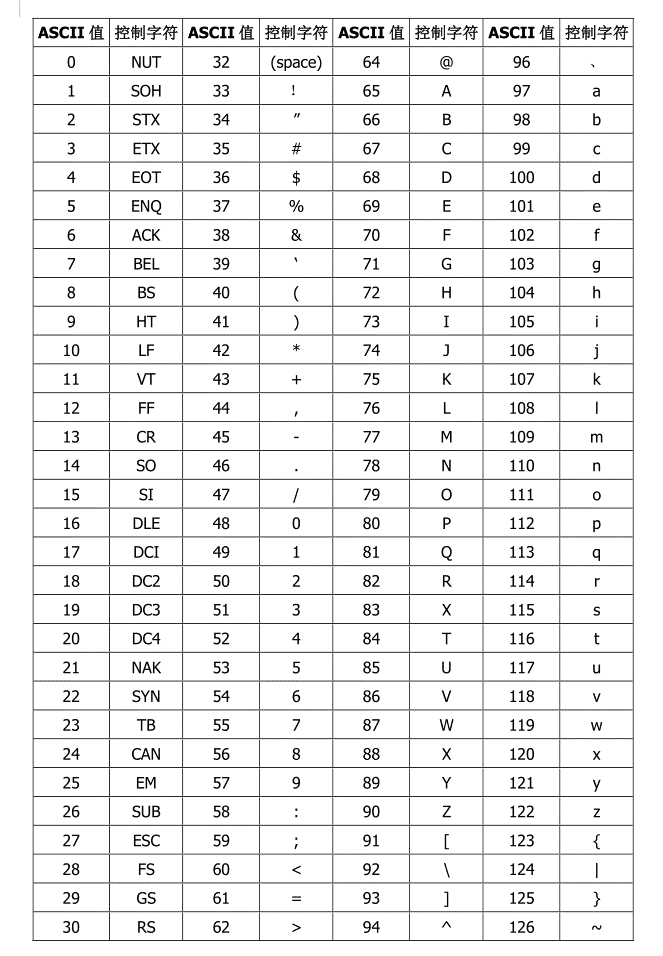
        这里涉及到很多char类型及ASCII表转换的操作，其中我们需要用到的：十进制48对应字符’0‘，十进制65对应字符’A‘，而A在进制中代表“10”，以此类推，话不多说直接上表。

（1）创建string及int类型对象

        用来接收输入的字符串,其中str用来接收不为10进制的数（可能会出现字母），sum_10有两个用处：1.若为十进制则直接赋值  2.若不为则用来接收其转为十进制后的值

string str;		//创建一个string对象，用于存储输入的字符串
	int base_pre = 10, base_curr = 10;		//初始化转换前的进制和转换后的进制
	int sum_10 = 0;		//初始化此数的十进制大小
    cout << "请输入转换前为几进制:";
	cin >> base_pre;

（2）判断输入的是否为十进制数

        若是十进制数则直接将输入的数赋值给sum_10,否则便将其转换为十进制，具体做法为遍历str。由于str[i]访问的单个字符为ASCII码值，它在计算时会调用其ASCII码值，而我们想要的是其字符里的值而不是其ASCII码值，为了方便我们直接在进行计算时减去一定的数。例如：‘6’在计算时会调用其ASCII码值54，我们将其减去48，就得到了我们想要的6。对于大于10的数来说要减去55，原因在之前也解释过，‘9’和‘A'中间隔了几个别的，’A’的ASCII码为65，所以大于’9‘的部分和小于’9‘的部分要分开计算。

        （temp-55）和（temp-48）便是上述操作，之后将其进行正常的转十进制数计算即可，其中pow（）函数是<cmath>库里的幂函数，第一个形参为底数，第二个形参为指数，注意^在C++里不是乘幂，而是位的运算。

if (base_pre == 10) {
		cin >> sum_10;		//输入的数若不为十进制则先转换为十进制
	}
	else{
		cin >> str;		//这里用str是确保进制大于十时也能全部读取(有字母)
		int max=str.size();			//定义该进制最大位数,方便后面进行计算
		for (int i = 0; i < str.size(); i++) {
			char temp=str[i];		//用char获取第i个字符的ASCII值(字符）
			if (temp > '9') {
				sum_10 = sum_10 + (temp - 55)*pow(base_pre,max-1);		//将ASCII码值还原成其对应的十进制值
			}		//因为'9'对应的十进制为57，而‘A’(也就是10)对应的十进制为65，所以要分别还原
			else sum_10 = sum_10 + (temp - 48)*pow(base_pre,max-1);		//将ASCII码值还原成其对应的十进制值

			max--;		//用来进行乘幂的位-1
		}
		cout << endl << "此数的10进制大小为:" << sum_10 << endl;
	}		//先将其转化为10进制

（3）将十进制转为任意进制

        转换步骤及代码都和上文介绍的方法匹配，需要注意的是我们在进栈时，要将余数转换成其对应字符的ASCII码值，之后输出时便可以通过ASCII码值输出数字或者字母（大于9）。这里这样操作是因为试过直接使用Stack<char>，输出时好像不能正常输出。所以便选择了Stack<int>，先将其字符对应的ASCII码存入，再通过ASCII码输出其字符。如果有更好的方法欢迎评论或私聊我。

        对了，这里最多支持35进制，因为一共就26个字母，A是10的代替。

cout << endl << "请输入转换后为几进制:";
	cin >> base_curr;		//输入要转换的位
	Stack<int> num_convert;		//创建一个栈用来存放取余后的数ASCII码值
	while (sum_10) {
		int temp;
		if (sum_10 % base_curr > 9) {
			temp = 64+sum_10 % base_curr - 9;		//取余	
		}		//和上文同样的，因为'9'对应的十进制为57，而‘A’(也就是10)对应的十进制为65，所以要分别计算其ASCII值
		else temp =48+sum_10 % base_curr;		//取余
		num_convert.push(temp);		//将计算好的数对应的ASCII值存入栈中
		sum_10=sum_10 / base_curr;		//取余后取除数
	}

（4）出栈完成转换

        将栈内元素逐个出栈，并输出其ASCII码值对应的字符便得到了转换以后的进制数。        

cout << "转换后的值为:";
	while (!num_convert.empty()) {
		char out= num_convert.top();		//创建一个char对象用来倒序输出栈内ASCII值对应的字符
		cout << out;
		num_convert.pop();		//输出后便出栈
	}
	cout << endl;

（5）封装成函数

        下面是整个操作的完整函数代码：

        如果不计Node和Stack的部分一共也才40来行，自夸是进制转换中最简洁的代码之一不过分吧（毕竟是任意转任意）。

void convert() {
	string str;		//创建一个string对象，用于存储输入的字符串
	int base_pre = 10, base_curr = 10;		//初始化转换前的进制和转换后的进制
	int sum_10 = 0;		//初始化此数的十进制大小
	cout << "请输入转换前为几进制:";
	cin >> base_pre;
	cout << endl << "请输入转换前的数字大小:";
	if (base_pre == 10) {
		cin >> sum_10;		//输入的数若不为十进制则先转换为十进制
	}
	else{
		cin >> str;		//这里用str是确保进制大于十时也能全部读取(有字母)
		int max=str.size();			//定义该进制最大位数,方便后面进行计算
		for (int i = 0; i < str.size(); i++) {
			char temp=str[i];		//用char获取第i个字符的ASCII值(字符）
			if (temp > '9') {
				sum_10 = sum_10 + (temp - 55)*pow(base_pre,max-1);		//将ASCII码值还原成其对应的十进制值
			}		//因为'9'对应的十进制为57，而‘A’(也就是10)对应的十进制为65，所以要分别还原
			else sum_10 = sum_10 + (temp - 48)*pow(base_pre,max-1);		//将ASCII码值还原成其对应的十进制值

			max--;		//用来进行乘幂的位-1
		}
		cout << endl << "此数的10进制大小为:" << sum_10 << endl;
	}		//先将其转化为10进制
	cout << endl << "请输入转换后为几进制:";
	cin >> base_curr;		//输入要转换的位
	Stack<int> num_convert;		//创建一个栈用来存放取余后的数ASCII码值
	while (sum_10) {
		int temp;
		if (sum_10 % base_curr > 9) {
			temp = 64+sum_10 % base_curr - 9;		//取余并转换成其对应字符的ASCII码	
		}		//和上文同样的，因为'9'对应的十进制为57，而‘A’(也就是10)对应的十进制为65，所以要分别计算其ASCII值
		else temp =48+sum_10 % base_curr;		//取余
		num_convert.push(temp);		//将计算好的数对应的ASCII值存入栈中
		sum_10=sum_10 / base_curr;		//取余后取除数
	}
	cout << "转换后的值为:";
	while (!num_convert.empty()) {
		char out= num_convert.top();		//创建一个char对象用来倒序输出栈内ASCII值对应的字符
		cout << out;
		num_convert.pop();		//输出后便出栈
	}
	cout << endl;
}

（6）main函数

        简洁明了，这就是抽象和封装的好处。

int main()
{
	convert();
}

三、完整代码

        以下是完整代码展示，由于个人水平有限，如有错误/不严谨的地方敬请指正。

#include <iostream>
#include <string>
#include <cmath>		//使用cmath的pow(幂运算)函数
using namespace std;
template<class T>class Stack;	//向前声明
template<class T>
class Node {
private:
	T m_data;	//数据域
	Node* m_next;	//指针域
public:
	Node(const T& val) {
		this->m_data = val;
	}	//有参构造
	Node& operator=(const Node& rhs) = delete;	//禁止赋值
	friend class Stack<T>;	//声明友元
};

template<class T>
class Stack {
private:
	Node<T>* m_top = nullptr;	//栈顶指针
public:
	Stack() = default;	//默认构造
	Stack(const Stack&) = delete;	//禁止复制
	Stack& operator=(const Stack&) = delete;	//禁止赋值
	~Stack() {
		clear();
	};	//析构
	void clear();	//清空栈
	void push(const T& val);	//入栈
	void pop();//出栈
	bool empty()const {
		return this->m_top == nullptr;
	}	//判断是否为空
	const T& top() {
		return this->m_top->m_data;
	}	//取出栈顶元素
};

template<class T>
void Stack<T>::push(const T& val) {
	Node<T>* node = new Node<T>(val);
	node->m_next = this->m_top;
	this->m_top = node;
}

template<class T>
void Stack<T>::pop() {
	if (empty()) {
		return;
	}
	Node<T>* p = this->m_top;
	this->m_top = this->m_top->m_next;
	delete p;
}

template<class T>
void Stack<T>::clear() {
	Node<T>* p = nullptr;
	while (this->m_top != nullptr) {
		p = this->m_top;
		this->m_top = this->m_top->m_next;
		delete p;
	}
}

void convert() {
	string str;		//创建一个string对象，用于存储输入的字符串
	int base_pre = 10, base_curr = 10;		//初始化转换前的进制和转换后的进制
	int sum_10 = 0;		//初始化此数的十进制大小
	cout << "请输入转换前为几进制:";
	cin >> base_pre;
	cout << endl << "请输入转换前的数字大小:";
	if (base_pre == 10) {
		cin >> sum_10;		//输入的数若不为十进制则先转换为十进制
	}
	else{
		cin >> str;		//这里用str是确保进制大于十时也能全部读取(有字母)
		int max=str.size();			//定义该进制最大位数,方便后面进行计算
		for (int i = 0; i < str.size(); i++) {
			char temp=str[i];		//用char获取第i个字符的ASCII值(字符）
			if (temp > '9') {
				sum_10 = sum_10 + (temp - 55)*pow(base_pre,max-1);		//将ASCII码值还原成其对应的十进制值
			}		//因为'9'对应的十进制为57，而‘A’(也就是10)对应的十进制为65，所以要分别还原
			else sum_10 = sum_10 + (temp - 48)*pow(base_pre,max-1);		//将ASCII码值还原成其对应的十进制值

			max--;		//用来进行乘幂的位-1
		}
		cout << endl << "此数的10进制大小为:" << sum_10 << endl;
	}		//先将其转化为10进制
	cout << endl << "请输入转换后为几进制:";
	cin >> base_curr;		//输入要转换的位
	Stack<int> num_convert;		//创建一个栈用来存放取余后的数ASCII码值
	while (sum_10) {
		int temp;
		if (sum_10 % base_curr > 9) {
			temp = 64+sum_10 % base_curr - 9;		//取余	
		}		//和上文同样的，因为'9'对应的十进制为57，而‘A’(也就是10)对应的十进制为65，所以要分别计算其ASCII值
		else temp =48+sum_10 % base_curr;		//取余
		num_convert.push(temp);		//将计算好的数对应的ASCII值存入栈中
		sum_10=sum_10 / base_curr;		//取余后取除数
	}
	cout << "转换后的值为:";
	while (!num_convert.empty()) {
		char out= num_convert.top();		//创建一个char对象用来倒序输出栈内ASCII值对应的字符
		cout << out;
		num_convert.pop();		//输出后便出栈
	}
	cout << endl;
}

int main()
{
	convert();
}

---

之后也会每周更新C++数据结构和算法的相关内容，将逐渐由浅入深，感兴趣的朋友可以点个赞和关注。