【C++数据结构】小球下落问题（二叉树）

问题描述： 

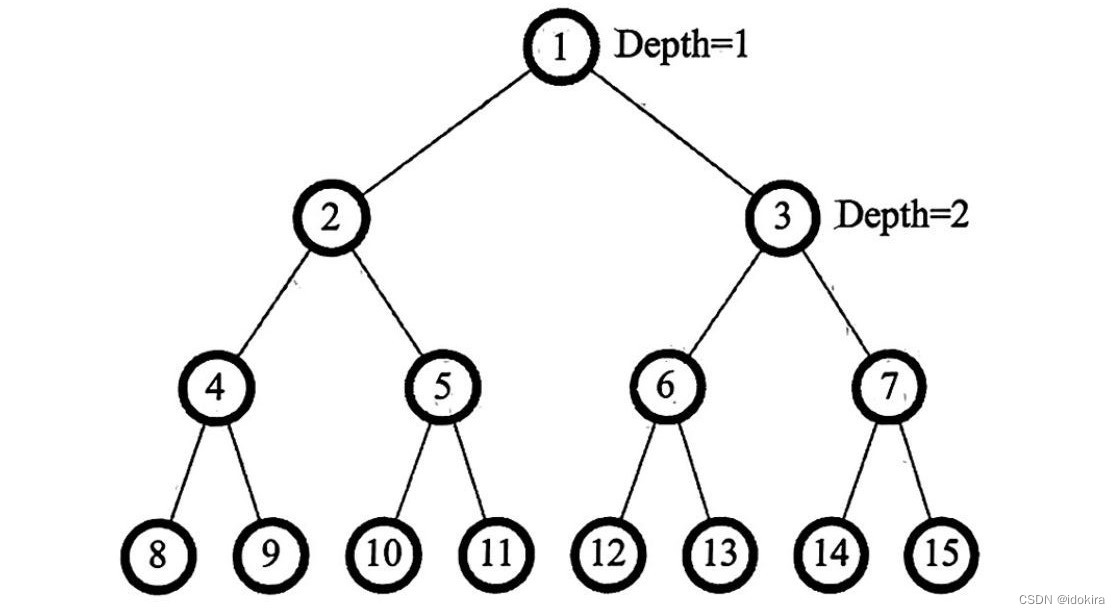
        有一棵二叉树，最大深度为 D，且所有叶子的深度都相同。所有结点从上到下从左到右编号为1,2,3,…,。在结点 1 处放一个小球，它会往下落。每个内结点上都有一个开关，初始全部关闭，当每次有小球落到一个开关上时，状态都会改变。当小球到达一个内结点时，如果该结点上的开关关闭，则往左走，否则往右走，直到走到叶子结点，如图所示。

       

         一些小球从结点1处依次开始下落，最后一个小球将会落到哪里呢?输入叶子深度 D 和小球个数 I，输出第 I 个小球最后所在的叶子编号。假设I不超过整棵树的叶子个数。20。输入最多包含1000组数据。

样例输入：

4 2

3 4
10 1

2 2

8 128

16 12345

样例输出：

12

7

512

3

255

36358

---

 提示：以下是本篇文章正文内容，代码注释较为详细，可供参考 

解决思路：

        不难发现，对于一个结点k，其左子结点、右子节点的编号分别是 2k 和 2k+1。 用数组存放结点，用结点的值 1/0 表示状态，模拟小球下落过程。可以写成下面的模拟程序：

        初始化数组并将每个结点置0表示每个结点初始往左落下，之后将该结点状态翻转并将 k 值更新为其左或右结点的编号（往下落）。重复这一过程直至 k 大于最大的叶子编号。

#include <iostream>
#include <cmath>
using namespace std;
int main()
{
	int D, I;		// 叶子深度D 小球个数I
	// 结点值为0代表向左，1为向右
	while (cin >> D >> I) {
		int node[1000000] = { 0 };	// 初始化一个数组用于存放每个结点，并将每个结点状态置0
		int k, n = pow(2, D);	// 定义根节点，以及最大的叶子编号
		for (int i = 0; i < I; i++) {
			k = 1;		// 每次下落时初始化根节点
			while (k < n) {
				int temp = node[k];		// 记录下此时结点状态用于判断方向
				node[k] = !node[k];		// 翻转该结点状态
				if (!temp) {
					k = k * 2;		// 为0往左
				}
				else k = k * 2 + 1;		// 为1往右
			}		// 重复直到k大于叶子编号
		}
		cout << k/2 << endl;	// 由于k大于编号才停止，我们要的是最后一次即大于前的结果
	}
}

         虽然该程序能够完美模拟并得到答案，但有一个缺点：运算量太大。由于 D 最大为 20，每组测试数据下落总层数可能会高达 9961472 次，而一共可能有 10000 组数据。

        所以不妨通过另外一种思路，对于每个结点来说，其第奇数个小球必定往左，其第偶数个小球必定往右。所以我们只需要不停验证其奇偶性便可以模拟任意一个小球下落的过程，即每遇到一个结点便验证该小球是第奇数个还是偶数个到该结点的小球，便可以知道下落方向。依次类推，直到遇到叶子上。

        这样，程序的运算量便与小球数量及编号无关了，并且节省了一个巨大的数组空间。程序如下：

#include <iostream>
#include <cmath>
using namespace std;

int main()
{
	int D, I;		// 叶子深度D 小球个数I
	while (cin >> D >> I) {
		int k = 1;		// 根节点
		for (int height = 1; height < D; height++) {
			if (I % 2) {
				k = k * 2;		// 若此小球是落入该结点的第奇数个小球，则往左走
				I = I / 2 + 1;		// 下一层结点的第(I/2+1)个小球，因为I是奇数所以/2后+1		
			}
			else {
				k = k * 2 + 1;		// 落入该结点的偶数个小球，往右走
				I = I / 2;			// 下一层结点的第(I/2)个小球
			}
		}		// 小球往下掉落D-1次
		cout << k << endl;
	}

}

       

---

之后也会每周更新C++数据结构和算法的相关内容，感兴趣的朋友可以点个赞和关注。