摆动数列详解

看代码熟悉一下 

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
int n = nums.size();
if(n < 2) return n;
int ret = 0, left = 0;
for(int i = 0;i < n - 1;i++)
{
    int right = nums[i + 1] - nums[i];
    if(right == 0)continue;
    if(right * left <= 0) ret++;
    left = right;
}
return ret + 1;

    }
};

如果此刻你能够用此代码倒推思路，我愿敬你为神！！

题目和思路

 思路:

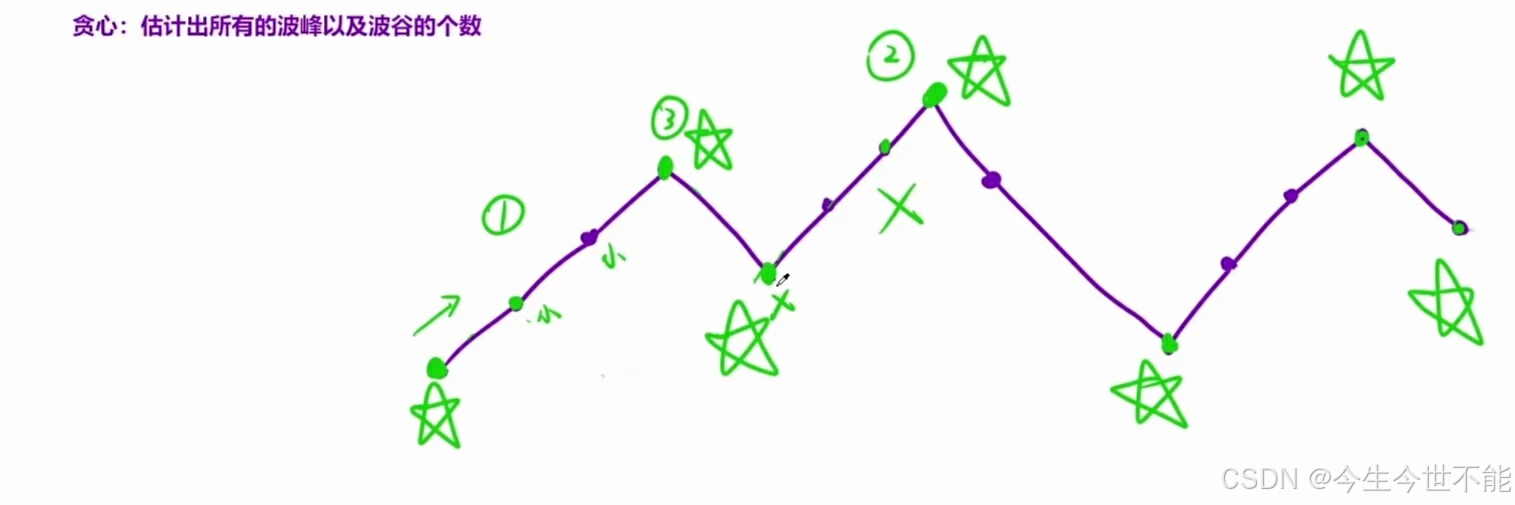
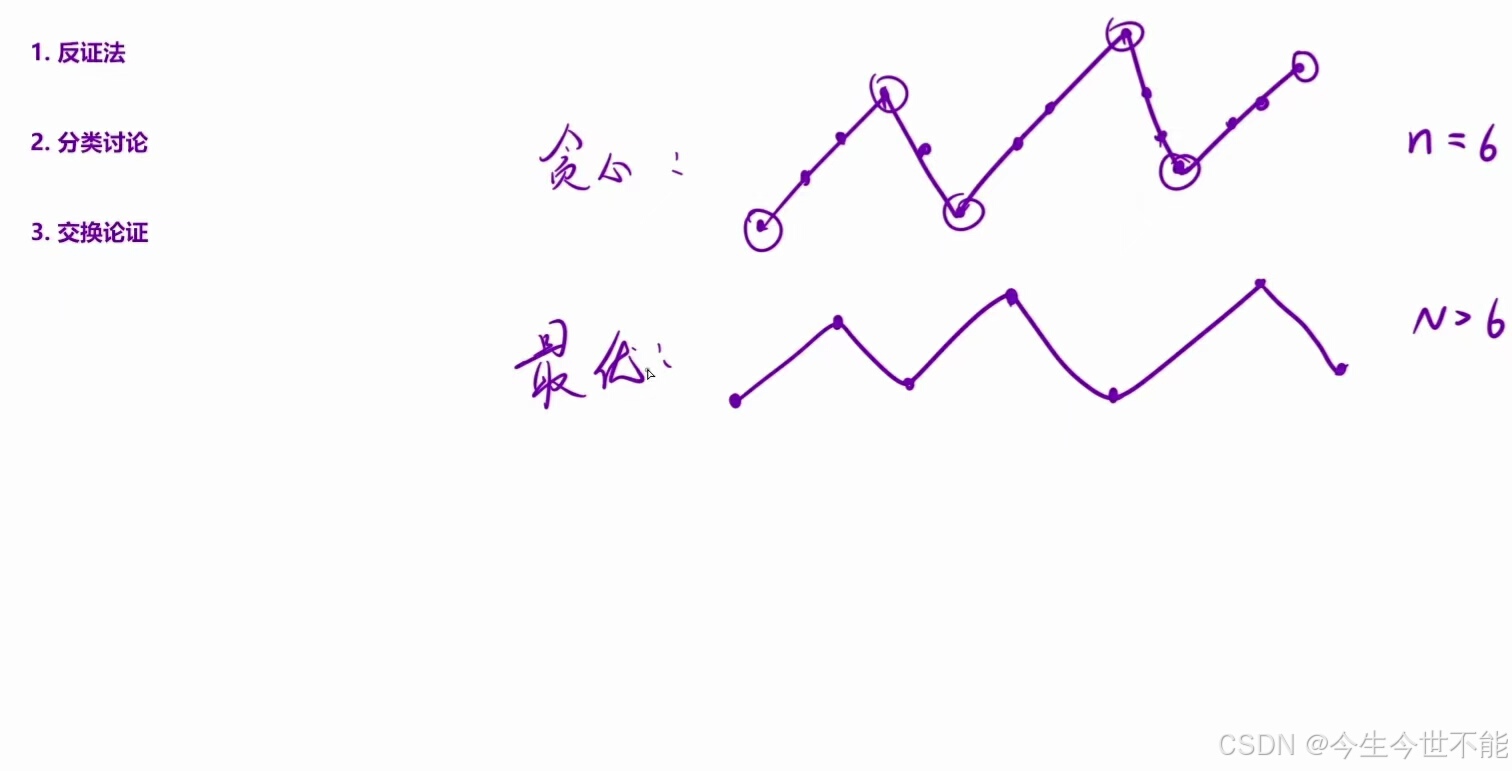
观察这个序列可以发现，我们不断地交错选择「峰」与「谷」，可以使得该序列尽可能长。证明非常简单：如果我们选择了一个「过渡元素」，那么在原序列中，这个「过渡元素」的两侧有一个「峰」和一个「谷」。不失一般性，我们假设在原序列中的出现顺序为「峰」「过渡元素」「谷」。如果「过渡元素」在选择的序列中小于其两侧的元素，那么「谷」一定没有在选择的序列中出现，我们可以将「过渡元素」替换成「谷」；同理，如果「过渡元素」在选择的序列中大于其两侧的元素，那么「峰」一定没有在选择的序列中出现，我们可以将「过渡元素」替换成「峰」。这样一来，我们总可以将任意满足要求的序列中的所有「过渡元素」替换成「峰」或「谷」。并且由于我们不断地交错选择「峰」与「谷」的方法就可以满足要求，因此这种选择方法就一定可以达到可选元素数量的最大值。

这样，我们只需要统计该序列中「峰」与「谷」的数量即可（注意序列两端的数也是「峰」或「谷」），但需要注意处理相邻的相同元素。

在实际代码中，我们记录当前序列的上升下降趋势。每次加入一个新元素时，用新的上升下降趋势与之前对比，如果出现了「峰」或「谷」，答案加一，并更新当前序列的上升下降趋势。

复杂度分析

• 时间复杂度：O(n)，其中 n 是序列的长度。我们只需要遍历该序列一次。

• 空间复杂度：O(1)。我们只需要常数空间来存放若干变量。

策略证明

 谢谢大家的观看！