二叉树的完美重建（玩转三种遍历）——（1）通过前序/后序遍历，中序遍历构建二叉树，（2）通过前序遍历， 后序遍历确定有多少不同形态的二叉树

二叉树的重建

提要： 建议看这篇之前先去了解二叉树的四种遍历方式前序遍历，中序遍历，后序遍历和层序遍历

问题引入：

通过给定我们一颗二叉树，我们可以实现对这颗二叉树的遍历

question 1 ： 我们已知哪几种遍历方式可以 唯一 的确定一颗二叉树？ 并且我们怎么确定这颗二叉树？

question 2 ： 如果我们已知的遍历方式 不能唯一的确定一颗二叉树， 那么可以有几种 不同形态的二叉树？

解决question 1

answer : 我们若已知中序遍历，前/后序遍历即可唯一的确定一颗二叉树

至于为什么唯一确定我们这里不深入探讨，只做简单说明：

唯一性:

前序遍历：唯一确定根节点的值 （前序遍历的第一个元素始终是当前子树的根节点）

中序遍历：唯一确定根节点的位置

so 这颗二叉树的每一步的划分都是唯一的，因此，从前序和中序遍历可以唯一确定出二叉树的结构。（后序和中序的组合也是同样道理）

下面给出两种代码实现

核心思想：

给出两种遍历方式 ——> 通过每次递增/减索引得到根节点从而新建一个节点 ——> 通过映射找到根节点在中序遍历中的位置

——> 递归构建 *左右（前序遍历）/ 右左（后序遍历） 子树

通过前序遍历和中序遍历递归构建二叉树

// 通过前序遍历和中序遍历递归构建二叉树

#include <iostream>
#include <vector>
#include <unordered_map>
#include <queue>
using namespace std;

// 用模板定义树节点
template <typename T>
struct node
{
    T val;
    node<T> *left;
    node<T> *right;
    node(T val) : val(val), left(nullptr), right(nullptr) {}
};

// 根据前序和中序遍历构造二叉树
// preIndex: 记录当前在前序遍历中的索引
// inStart 和 inEnd : 确定当前递归的中序遍历子数组的范围
// inMap : 用来快速查找元素在中序遍历中的位置
node<int> *buildTree_by_preAndIn(const vector<int> &preorder, const vector<int> &inorder, int &preIndex, int inStart, int inEnd, unordered_map<int, int> &inMap)
{
    // 如果当前子树的中序范围无效（即开始索引大于结束索引），则返回空指针，表示没有子树
    if (inStart > inEnd)
        return nullptr;

    // 获取当前根节点的值并新建一个节点
    int rootVal = preorder[preIndex++]; // 前序遍历的第一个元素总是树的根。
    node<int> *root = new node<int>(rootVal);

    // 在中序遍历中找到根节点的位置
    int index = inMap[rootVal];

    // 递归构建左子树和右子树
    // 前序遍历————先构建左子树，后构建右子树！！！！！！！
    root->left = buildTree_by_preAndIn(preorder, inorder, preIndex, inStart, index - 1, inMap);
    root->right = buildTree_by_preAndIn(preorder, inorder, preIndex, index + 1, inEnd, inMap);

    return root;
}

// 遍历
void levelOrder(node<int> *root)
{
    if (root == nullptr)
        return;

    queue<node<int> *> q;
    q.push(root);

    while (!q.empty())
    {
        node<int> *frt = q.front();
        q.pop();

        cout << frt->val << " ";

        if (frt->left != nullptr)
            q.push(frt->left);
        if (frt->right != nullptr)
            q.push(frt->right);
    }
    cout << endl;
}
void inOrder(node<int> *root)
{
    if (root == nullptr)
        return;

    inOrder(root->left);
    cout << root->val << " ";
    inOrder(root->right);
}

// 清理内存函数
void deleteTree(node<int> *root)
{
    if (root == nullptr)
        return;

    deleteTree(root->left);
    deleteTree(root->right);
    delete root;
}

// 测试函数
int main()
{
    // 输入前序遍历和中序遍历和后序遍历(可以根据需要改变输入)
    vector<int> preorder = {1, 2, 4, 5, 3, 6, 7}; // 前序遍历
    vector<int> inorder = {4, 2, 5, 1, 6, 3, 7};  // 中序遍历

    // 使用哈希表(unordered_map<int, int>)记录中序遍历元素的索引，快速查找元素的位置
    unordered_map<int, int> inMap;
    for (int i = 0; i < inorder.size(); i++)
        inMap[inorder[i]] = i;

    // 根据前序遍历和中序遍历构造二叉树
    int preIndex = 0;
    node<int> *root = buildTree_by_preAndIn(preorder, inorder, preIndex, 0, inorder.size() - 1, inMap);

    // 输出结果
    //中序遍历
    cout << "inOrder: ";
    inOrder(root);
    cout << endl;
    //层序遍历
    cout << "levelOrder: ";
    levelOrder(root);
    cout << endl;

    // 清理内存
    deleteTree(root);

    return 0;
}

通过后序遍历和中序遍历递归构建二叉树

#include <iostream>
#include <vector>
#include <unordered_map>
#include <queue>
using namespace std;

// 模板定义树节点
template <typename T>
struct node
{
    T val;
    node<T> *left;
    node<T> *right;
    node(T val) : val(val), left(nullptr), right(nullptr) {}
};

// 根据后序和中序遍历构造二叉树
// postIndex: 记录当前在后序遍历中的索引
// inStart 和 inEnd : 确定当前递归的中序遍历子数组的范围
// inMap : 用来快速查找元素在中序遍历中的位置
node<int> *buildTree_by_postAndIn(const vector<int> &postorder, const vector<int> &inorder, int &postIndex, int inStart, int inEnd, unordered_map<int, int> &inMap)
{
    // 如果当前子树的中序范围无效（即开始索引大于结束索引），则返回空指针，表示没有子树
    if (inStart > inEnd)
        return nullptr;

    // 获取当前根节点的值并新建一个节点
    int rootVal = postorder[postIndex--]; // 后序遍历的最后一个元素总是树的根。
    node<int> *root = new node<int>(rootVal);

    // 在中序遍历中找到根节点的位置
    int index = inMap[rootVal];

    // 递归构右子树和左子树
    // 后序遍历————先构建右子树，后构建左子树！！！！！！！！！
    root->right = buildTree_by_postAndIn(postorder, inorder, postIndex, index + 1, inEnd, inMap);
    root->left = buildTree_by_postAndIn(postorder, inorder, postIndex, inStart, index - 1, inMap);

    return root;
}

//遍历
void levelOrder(node<int> *root)
{
    if (root == nullptr)
        return;

    queue<node<int> *> q;
    q.push(root);

    while (!q.empty())
    {
        node<int> *frt = q.front();
        q.pop();

        cout << frt->val << " ";

        if (frt->left != nullptr)
            q.push(frt->left);
        if (frt->right != nullptr)
            q.push(frt->right);
    }
    cout << endl;
}
void inOrder(node<int> *root)
{
    if (root == nullptr)
        return;

    inOrder(root->left);
    cout << root->val << " ";
    inOrder(root->right);
}

// 清理内存函数
void deleteTree(node<int> *root)
{
    if (root == nullptr)
        return;

    deleteTree(root->left);
    deleteTree(root->right);
    delete root;
}

int main()
{
    // 输入前序遍历和中序遍历和后序遍历(可以根据需要改变输入)
    vector<int> postorder = {4, 5, 2, 6, 7, 3, 1}; // 后序遍历
    vector<int> inorder = {4, 2, 5, 1, 6, 3, 7};   // 中序遍历

    // 使用哈希表(unordered_map<int, int>)记录中序遍历元素的索引，快速查找元素的位置
    unordered_map<int, int> inMap;
    for (int i = 0; i < inorder.size(); i++)
        inMap[inorder[i]] = i;

    // 根据前序遍历和中序遍历构造二叉树
    int postIndex = postorder.size() - 1;
    node<int> *root = buildTree_by_postAndIn(postorder, inorder, postIndex, 0, inorder.size() - 1, inMap);

    // 输出结果
    cout << "inOrder: ";
    inOrder(root);
    cout << endl;

    cout << "levelOrder: ";
    levelOrder(root);
    cout << endl;

    // 清理内存
    deleteTree(root);

    return 0;
}

细心阅读代码的朋友可能已经发现一个容易出错的小细节

我们用前序遍历和中序遍历递归构建二叉树时是 先左子树后右子树

我们用后序遍历和中序遍历递归构建二叉树时是 先右子树后左子树

原因就在于：

前序遍历（Postorder）：根节点 -> 左子树 -> 右子树 
后序遍历（Inorder）：左子树 <- 右子树 <- 根节点

---

---

解决question 2

如果我们只是已知前序遍历和后序遍历，而不知道中序遍历，我们肯定无法唯一的确定一颗二叉树，但是二叉树形态肯定是有限的，那究竟有多少个不同形态，怎么求出这些不同的形态呢

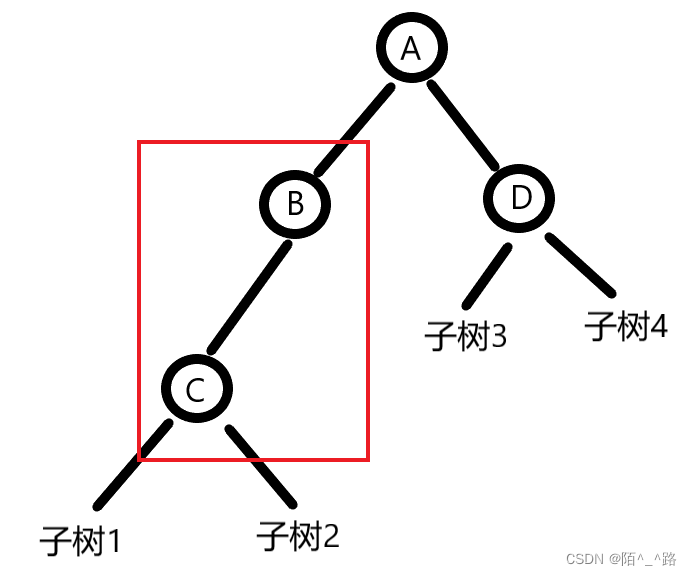
思考过程（非常有助于理解的推导思路）：

由于我们不知道中序遍历，我们就无法唯一的确定二叉树，那么中序遍历有哪些特别的作用？

没错，特别的作用就是我们前面提到的它可以唯一确定根的位置，那么现在我们显然不能唯一确定根的位置，也就是说根可能有左右两个位置，也就是说一棵子树的根可能是左子树的根也可能是右子树的根，也就是说此时的根节点只有一个子树，那么我们怎么通过两个遍历序列（前和后）判断此时的根节点 只有一个子树 呢？

我们又知道构建二叉树时，我们的索引指针前序遍历的顺序是根节点 -> 左子树 -> 右子树，后序遍历的顺序是根节点 -> 右子树 -> 左子树，由于我们前提一直是元素无重复，所以不可能左右根节点值相同，所以如果相同，那么就必然只有一个根节点，即如果 判断 pre[0 + 1] == post[(post.size() - 1) - 1] 为真，就说明左右根节点相同

方案一：

特判：

（1） 如果当前序列只有两个元素很明显它满足只有一个子树的条件，直接 res 加 1 返回。

（2） 如果当前序列少于两个元素很明显它没有不同的形态，直接返回

正常情况：

1. 给出前序和后续遍历序列，从根节点开始，依次查找该节点的左右子树的根节点是否相同（即检查当前根节点是否只有一个子树）leftSubTree_Node == rightSubTree_Node

依旧按照上图所示的例子，就可以发现左子树的根节点就在前序遍历的第二个位置，右子树的根节点就在后序遍历的倒数第二个位置（此时是不相等的情况，即此时有两颗子树）

1. 如果相同，递归遍历那唯一的一颗子树（前序nextPre和后序nextPost遍历序列）

2. 如果不相同，分别递归遍历左右两颗子树（左子树前序leftSubTree_pre和左子树后序leftSubTree_post, 右子树前序rightSubTree_pre, 右子树后序rightSubTree_post）

#include <iostream>
#include <string>
#include <cmath>
using namespace std;

int res = 0;
void CountDiffShape(const string &pre, const string &post)
{   
    //当前序列少于两个元素很明显它没有不同的形态，直接返回
    if (pre.length() < 2)
        return;
    //当前序列只有两个元素很明显它满足只有一个子树的条件，直接 res 加 1 返回
    if (pre.length() == 2)
    {
        res++;
        return;
    }

    // 左右子树的根节点
    char leftSubTree_Node = pre[1], rightSubTree_Node = post[post.length() - 2];

    // 判断左右子树的根节点是否相同
    // 最终目的：找只有一颗子树的情况（因为此时中序遍历结果不唯一———>有两种情况）

    // 左右子树的根节点相同————>只有一颗子树————>res++————>递归遍历该子树
    if (leftSubTree_Node == rightSubTree_Node)
    {
        res++;
        //nextPre : 唯一的子树的前序遍历序列, newtPost : 唯一的子树的后序遍历序列
        string nextPre = pre.substr(1, pre.length() - 1), nextPost = post.substr(0, post.length() - 1);
        // 递归遍历子树
        CountDiffShape(nextPre, nextPost);
    }
    else
    { /*
		Q YUIO PAS
		OIUY ASP Q
      */
        // 左右子树的根节点不同————>有左右两颗子树————>将pre，post分割为左右两颗子树的pre,post（4个子段）————>递归遍历所有子树
        string leftSubTree_pre, leftSubTree_post, rightSubTree_pre, rightSubTree_post;
        // 分割为左右两颗子树的pre
        for (int i = 1; i < pre.length(); i++)
        {
            if (pre[i] == rightSubTree_Node)
            {
                leftSubTree_pre = pre.substr(1, ((i - 1) - 1) + 1), rightSubTree_pre = pre.substr(i, ((pre.length() - 1) - i) + 1);
                break;
            }
        }
        // 分割为左右两颗子树的post
        for (int i = post.length() - 2; i >= 0; i--)
        {
            if (post[i] == leftSubTree_Node)
            {
                leftSubTree_post = post.substr(0, (i - 0) + 1), rightSubTree_post = post.substr(i + 1, ((post.length() - 2) - (i + 1)) + 1);
                break;
            }
        }
        // 递归遍历左右两颗子树
        CountDiffShape(leftSubTree_pre, leftSubTree_post);
        CountDiffShape(rightSubTree_pre, rightSubTree_post);
    }
}

//test function
int main()
{
    string pre, post;
    cin >> pre >> post;
    CountDiffShape(pre, post);
    cout << (int)pow(2, res) << endl;
    return 0;
}

方案二：（优化）

1. 我们将算法进一步抽象，由于一棵树的根节点唯一，即前序遍历第一个值和后序遍历的最后一个值必然相同；

2. 我们找的条件是左右子树的根节点相同，也就是前序遍历第二个值和后序遍历的倒数第二个值相同；

3. 综上，如果说前序遍历正序连续两个值和后序遍历逆序连续两个值如果相同，就说明出现了子树唯一的情况

4. 所以我们只需查找字符串即可

话不多说上代码

#include <iostream>
#include <string>
#include <cmath>
using namespace std;
int res = 0;
int main()
{
    string pre, post;
    cin >> pre >> post;
    for (int i = 0; i < pre.length() - 1; i++)
    {
        string temp;
        //因为是逆序相等，比如说 AB CDRFTG 和 GFTRDC BA
        temp += pre[i + 1], temp += pre[i];
        //如果前序遍历正序连续两个值和后序遍历逆序连续两个值相同
        if (post.find(temp) != -1)
            //结果加一
            res++;
    }
    cout << (int)pow(2, res);
    return 0;
}

补充说明

至于为什么最后结果需要 (int)pow(2, res)，是因为

我们找到 n 个满足只有唯一子树的节点，有 n 个不同的满足情况节点的话就有 2^n 种不同的树满足给定的前序遍历和后序遍历

特别鸣谢博主 陌 ^^-^路的图支持