目录
1.随机变量分布函数和分布律
定义：X是一个随机变量，F(x) = P(X<=x) -无穷<x<+无穷
根据概率的性质，F(x)也是 大于等于0小于等于1的
利用分布函数求各种随机事件的概率
↓下面这些请自己画线段图推一下
例题：用分布函数求概率
根据我们上面推的第五个式子
故选C
分布函数的性质
①.非负性. 0=<F(X)<=1
②.规范性 当x等于负无穷 F(x)=0 当x等于正无穷 F(x)=1;
③.单调不减性 对于任意x1<x2,F(x1)<F(x2)
④.右连续性 F(x0+0)=F(x0)
注：上述1和4性质可以用来判断我们的函数是不是分布函数。而性质3，4是可以求未知的参数的。
例题1 利用分布函数的性质来判断函数是否为分布函数
例题2 判断分布函数运算之后还是不是分布函数
A选项当x等于正无穷的时候 F1(x)=F2(x) = 1 F1(x)+F2(x) = 2（分布函数规范性要求F（正无穷）=1
B选项同理 G（x）= F1(x)+F2(x) G（正无穷）=0 同上不符合规范性
C选项 不符合分布函数的单调不减性，F1（x）和F2（x）都是单调不减函数，如果乘起来就不一定是单调不减的了，举个例子比如-x乘-2x 结果2x² 二次函数不是单调不减的
D选项，符合规范性，单调不减+单调不减 结果还是单调不减的，符合单调性，故选D
例题3：利用右连续求未知参数
计算分布律
离散型随机变量的分布律：设X为离散型随机变量，X的可能取值为x1,x2.....xk.....
例题 求分布律
三步骤①定取值 ②算概率 ③验证1
例题 求分布律2
例题：求分布律3
根据分布律求分布函数
以这个分布律为例，我们把它变成分布函数
有了这个分布函数，我们求概率就更方便了
例题
2.常见的离散型分布
二项分布
二项分布定义 A在任意一次实验中出现的概率都是相同的，X表示在n重伯努利实验中A成功的次数，其所有的可能取值为0，1，2，3，4，...n 相应的概率为：
记作X~B(n,p)
例题
例题2；
泊松分布
泊松分布定义 ：概率分布如下图
记作X~P(λ)
就称之为泊松分布
例题：泊松分布
几何分布（了解
超几何分布（了解）
泊松定理
泊松定理就是当我们二项分布的实验次数很多的话就能近似成泊松分布求解
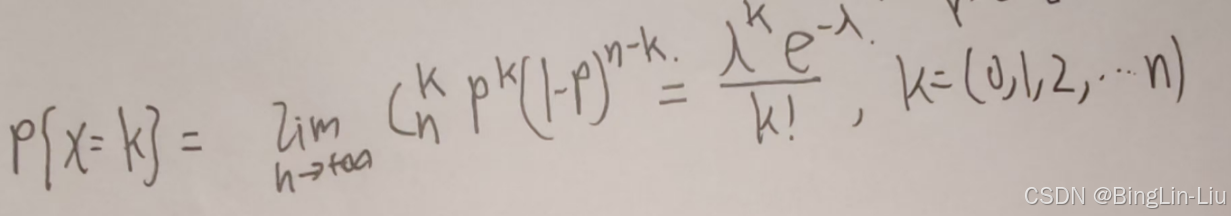
泊松定理例题：
3.一维连续性随机变量及其分布
概率密度函数的性质
①非负性：f(x) >=0 负无穷<x<正无穷
②规范性：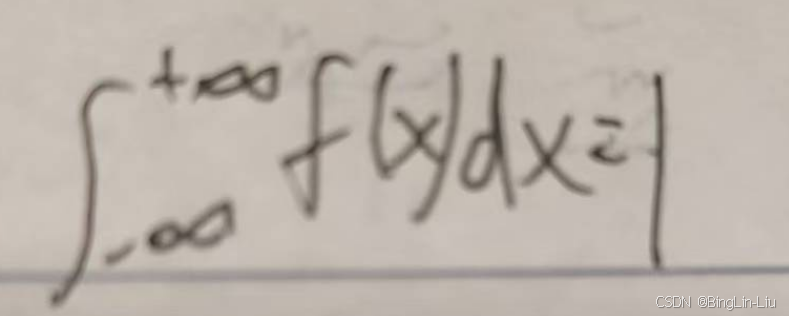
性质2可以求位置参数，
例题1：已知密度函数，求分布函数
利用密度概率函数的性质求未知参数‘？
用密度函数的规范性和非负性判断是不是密度函数
4.常见的连续性随机变量
均匀分布
如果随机变量的概率密度X是
则称X在[a,b]上服从均匀分布
记作X~u（a,b)
均匀分布算概率例题
指数分布
如果随机变量X的概率密度为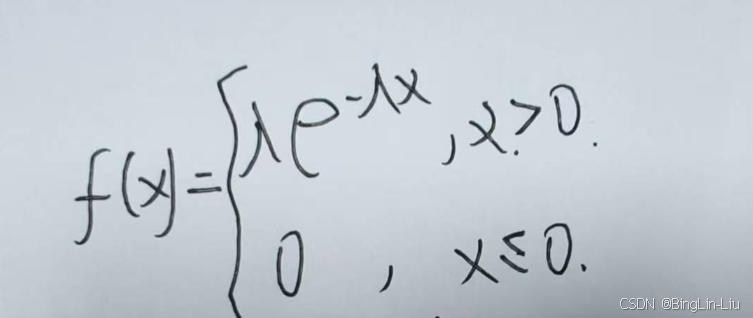
则称X为符合λ的指数分布 记作X~E（λ）
我们只需要记住它的分布函数就能做题了
指数分布算概率例题
指数分布算概率例题2
利用指数分布的概率密度算积分的小技巧
正态分布
如果随机变量X的概率密度为
就称它是正态分布
记作
利用概率密度性质求积分小技巧2
正态分布（给你 概率 求u）
啥是标准正态？
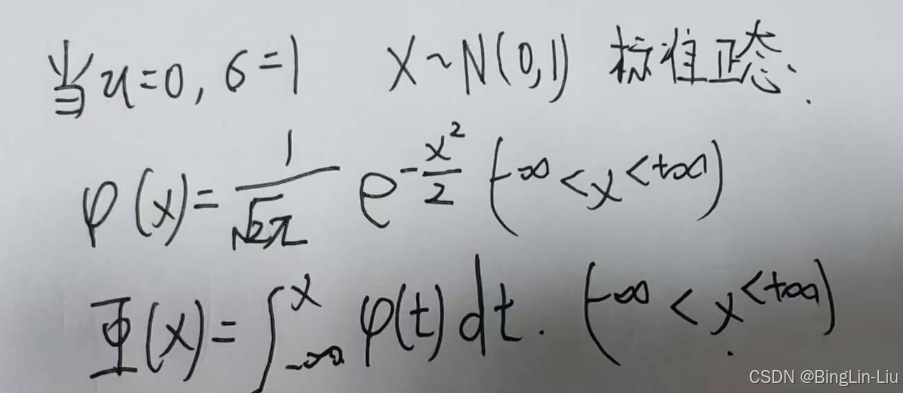
正态分布有啥性质？
性质1：对称性
上α分位点
例题
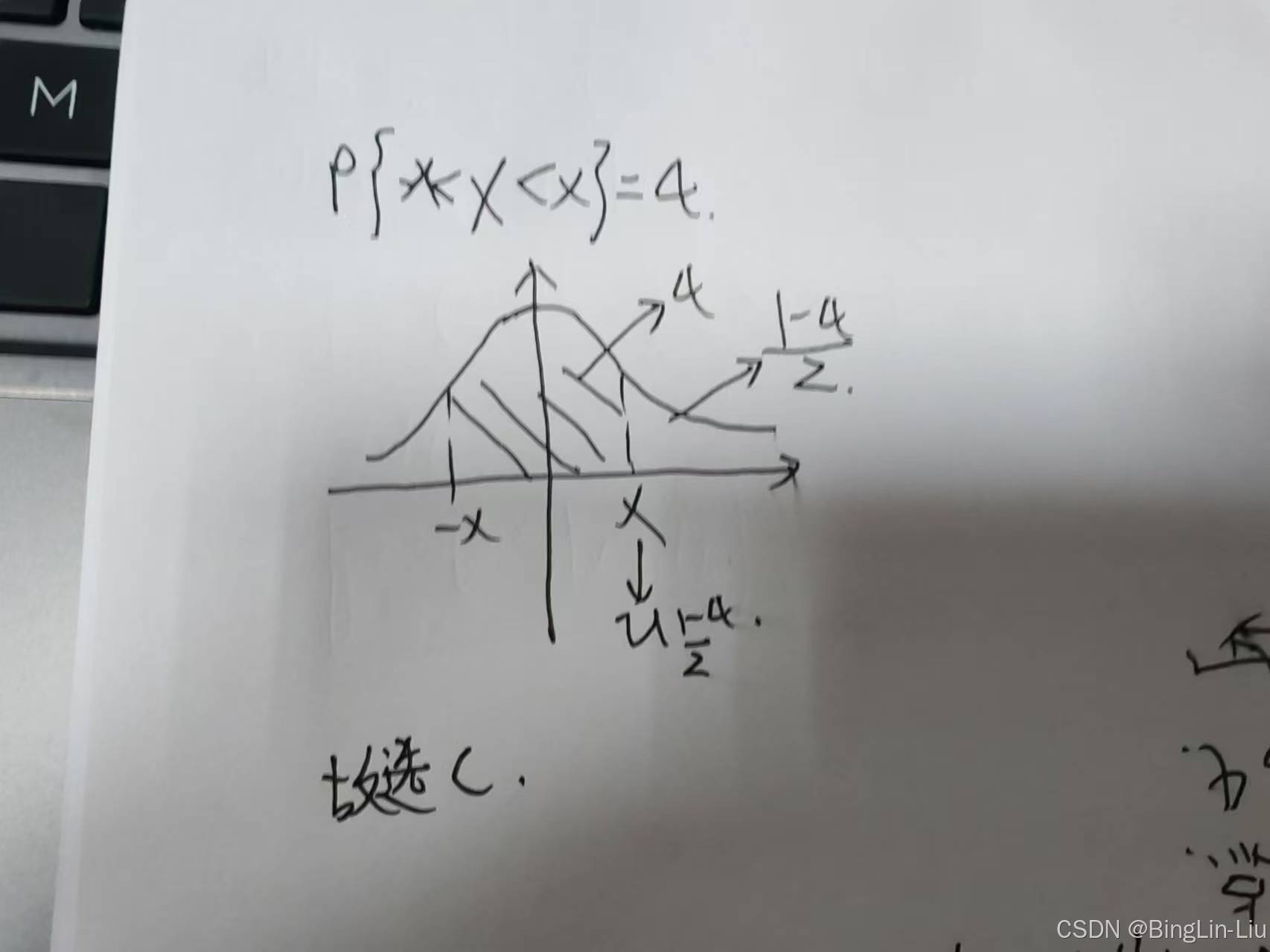
例题2
‘解决问题时进行标准化
解决正态分布问题，1。标准化 2.利用对称性 3.查表计算
例题 标准化并利用标准正态的对称性
例题2 标准化并利用标准正态的对称性
5.随机变量函数的分布
例题1：
怎么找范围？
根据X找到Y的边缘点
例题2：
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
