红黑树和递归树

1. 红黑树（R-B Tree）

1.1. 平衡二叉查找树

背景：

普通二叉查找树（BST）问题：

在频繁插入/删除的动态更新场景下，BST 可能退化为链表，时间复杂度从 O(logn) 退化到 O(n)。

解决方案：

引入平衡二叉查找树，通过保持树的结构“相对平衡”以控制树高，避免性能退化。

平衡二叉树：

二叉树中任意节点的左右子树高度差 ≤ 1。

完全二叉树、满二叉树其实都是平衡二叉树，但是非完全二叉树也有可能是平衡二叉树。

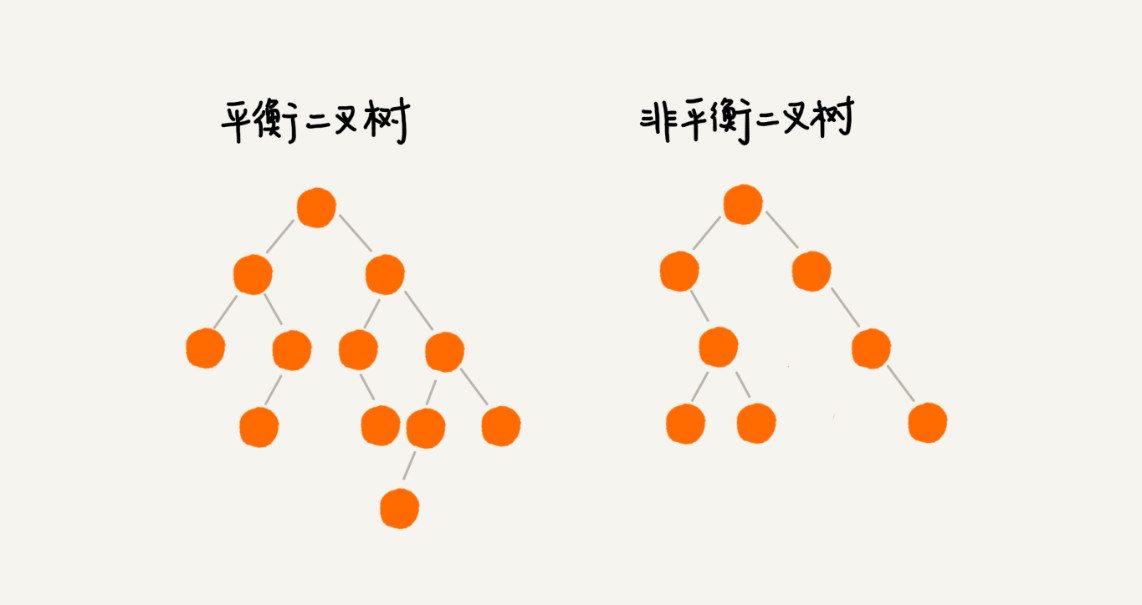
平衡二叉查找树不仅满足上面平衡二叉树的定义，还满足二叉查找树的特点。最先被发明的平衡二叉查找树是AVL 树，它严格符合我刚讲到的平衡二叉查找树的定义，即任何节点的左右子树高度相差不超过 1，是一种高度平衡的二叉查找树。

但是很多平衡二叉查找树其实并没有严格符合上面的定义（树中任意一个节点的左右子树的高度相差不能大于 1），比如下面要讲的红黑树，它从根节点到各个叶子节点的最长路径，有可能会比最短路径大一倍。

发明平衡二叉查找树这类数据结构的初衷是，解决普通二叉查找树在频繁的插入、删除等动态更新的情况下，出现时间复杂度退化的问题。

平衡二叉查找树：

平衡二叉查找树中“平衡”的意思，其实就是让整棵树左右看起来比较“对称”、比较“平衡”，不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些，相应的插入、删除、查找等操作的效率高一些。

所以，如果我们现在设计一个新的平衡二叉查找树，只要树的高度不比 log2n 大很多（比如树的高度仍然是对数量级的），尽管它不符合我们前面讲的严格的平衡二叉查找树的定义，但我们仍然可以说，这是一个合格的平衡二叉查找树。

平衡二叉查找树常见类型：

• AVL 树（严格平衡）
• 红黑树（近似平衡）
• Splay Tree（伸展树）
• Treap（树堆）

2.2. 红黑树

红黑树简介：

红黑树（Red-Black Tree，简称 R-B Tree）是最常用的平衡二叉查找树之一。

为什么工程中广泛使用红黑树？

• 性能稳定，不易退化。
• 维护平衡的代价相对较低，适合频繁更新。
• 插入、删除、查找操作的时间复杂度稳定在 O(logn)。

红黑树的定义：

• 每个节点要么是红色要么是黑色。
• 根节点是黑色。
• 每个叶子节点是黑色的空节点（NIL）。（实现细节中使用）
• 每个红色节点的两个子节点必须是黑色。（无连续红色节点）
• 从任意节点到其所有叶子节点的路径上，都包含相同数目的黑色节点（黑高一致）。

2.3. 红黑树的近似平衡

“平衡”的意思可以等价为性能不退化。“近似平衡”就等价为性能不会退化的太严重。

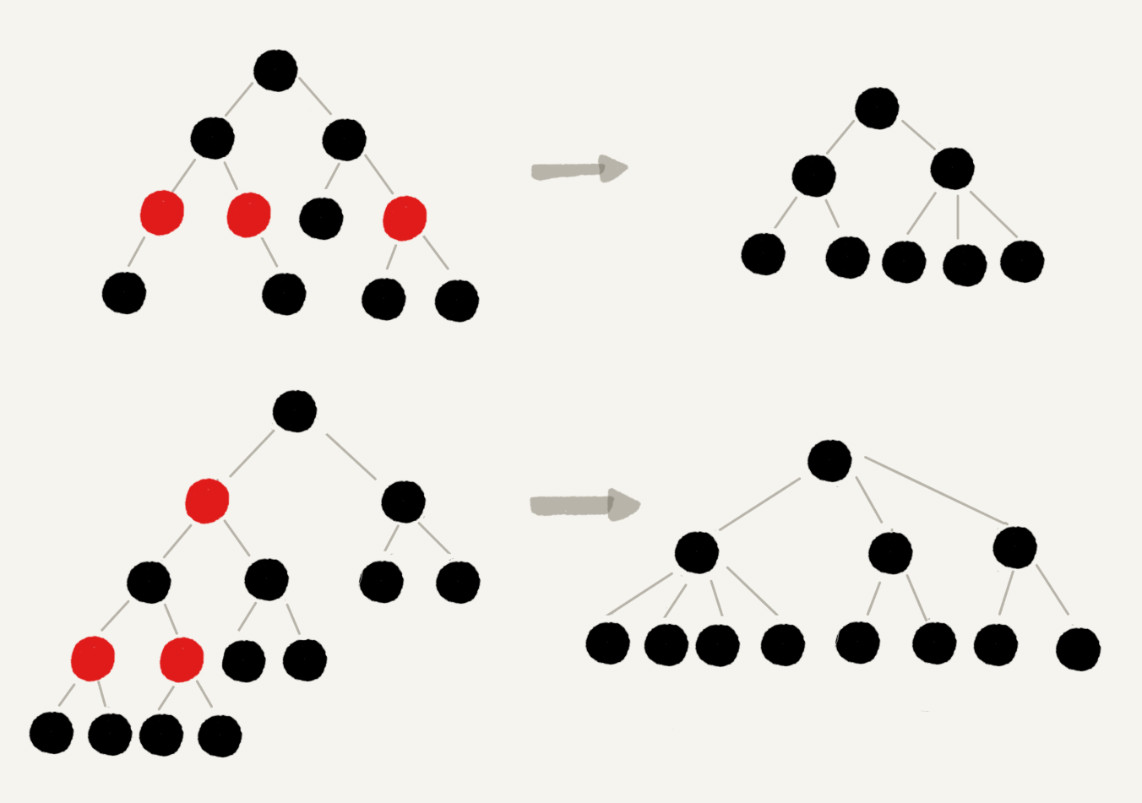
删除红色节点后：
红黑树只剩黑色节点，形成更低的“四叉黑树”，比同样规模的完全二叉树还要矮，即黑树高度≤log2n。

加上红色节点，红色节点不能连续：
最长路径中红黑交替，因此红黑树的最大高度为 2log₂n。

平衡二叉搜索树对比：

数据结构	平衡程度	插入/删除成本	查找效率	工程适用性
AVL 树	高度平衡	高	高	中
红黑树	近似平衡	低	高	高 ✅
Splay Tree	无严格平衡	低（摊还）	平均高	中
Treap	基于随机性	低	平均高	中

• 红黑树牺牲一部分极致平衡，换来了维护效率和性能稳定性，更适用于工程应用。

2.4. 红黑树的实现

红黑树是一种自平衡的二叉查找树，其实现的核心目标是通过控制节点的颜色和树的旋转操作，在插入和删除过程中维持树的平衡，从而保证查找、插入、删除操作的时间复杂度始终为 O(log n)。

左旋 （rotate left）和右旋 （rotate right） ：

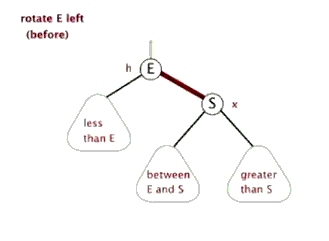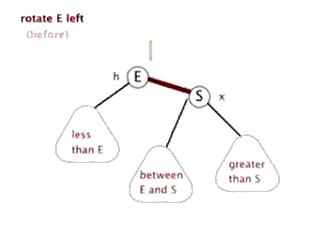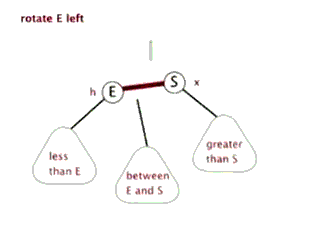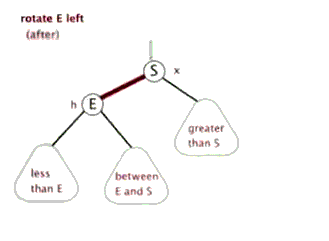
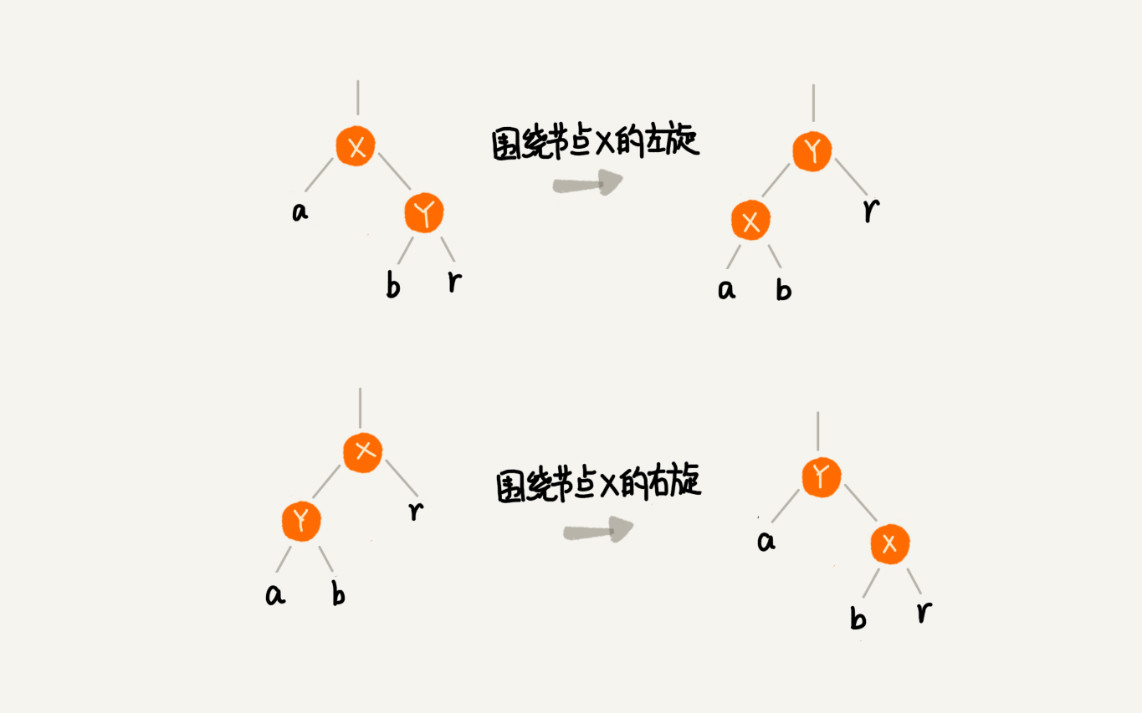
红黑树实现的关键特点：

1. 节点着色规则：每个节点非红即黑，根节点始终为黑色，红色节点不能相邻，所有从任一节点到其所有叶子节点的路径上黑色节点数量相同。
2. 引入哨兵 NIL 节点：每个叶子节点为一个黑色的空节点，用于统一处理逻辑，简化实现。
3. 插入与删除时的调整机制：通过颜色变换和左旋、右旋操作，确保插入或删除后树的性质不被破坏。
4. 左旋与右旋操作：用以局部调整子树结构，恢复红黑树的平衡状态。
5. 关注节点策略：插入或删除后以“关注节点”为核心，逐步迭代调整直到树重新满足红黑树的定义。

总体而言，红黑树通过结构规则和动态调整，兼顾了有序性和近似平衡性，是许多底层数据结构（如 Java 的 TreeMap、C++ 的 map）背后的核心机制。

2. 用递归树计算递归算法的时间复杂度

2.1. 递归树的概念

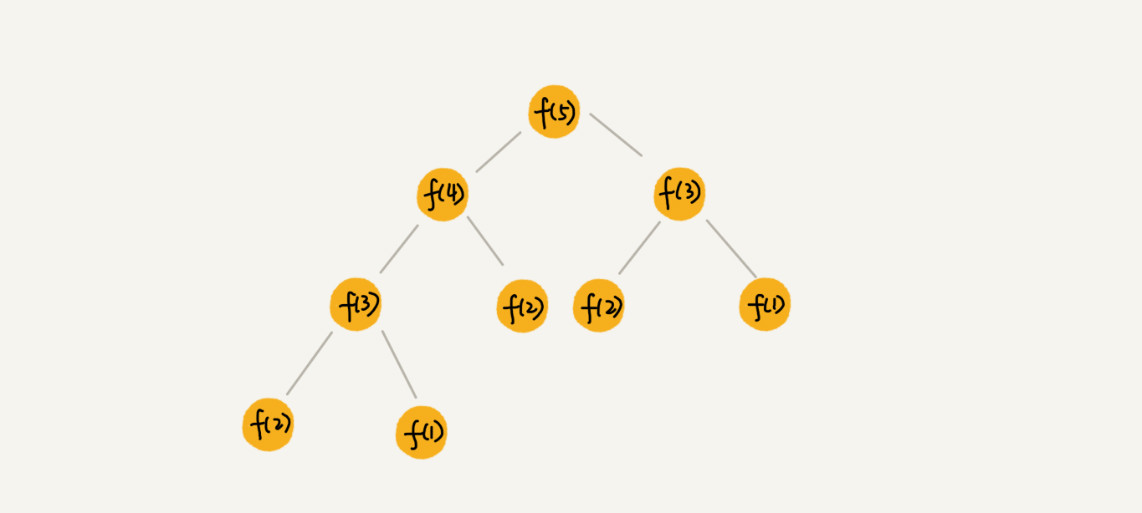
递归树的概念：

• 递归树是一种将递归调用过程图形化的工具，把每次递归分解看作一棵树的节点；
• 每层代表一次递归的“深度”，每个节点表示一次函数调用及其所消耗的时间；
• 总体时间复杂度 = 每层的总时间 × 树的高度。
• 总体时间复杂度 = 每层的总时间之和

2.2. 递归树求解时间复杂度实战

1. 归并排序

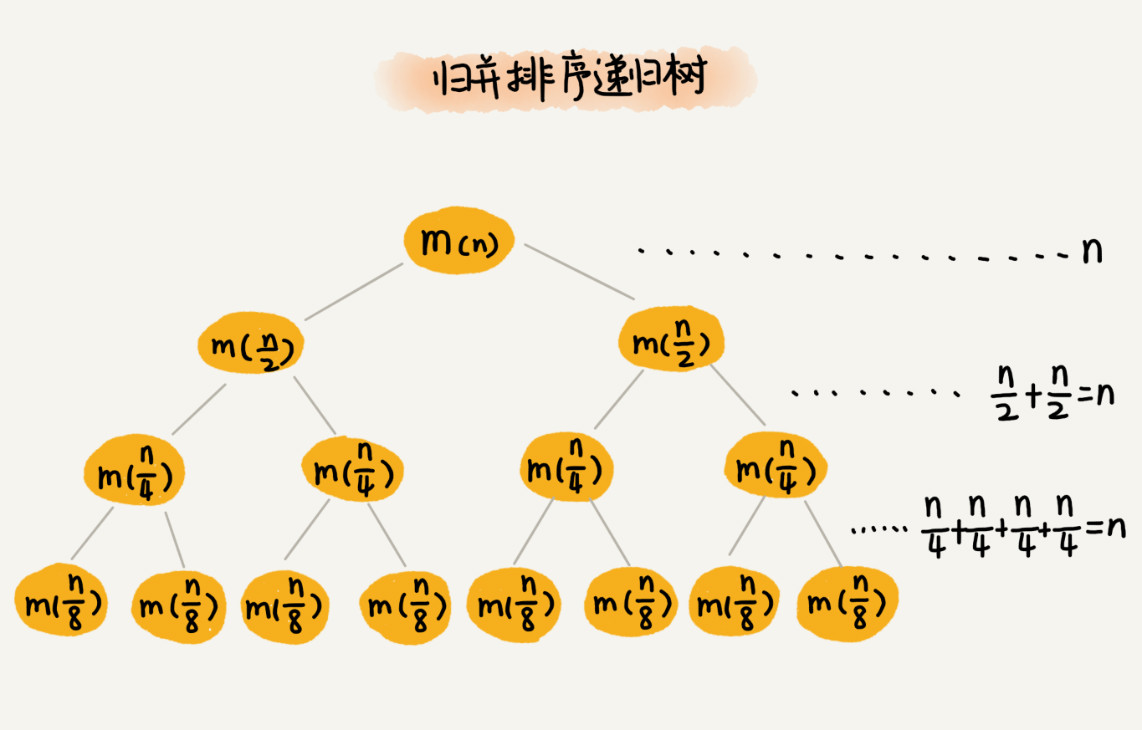
• 每次一分为二，递归树为满二叉树；
• 每层归并要处理的总数据量为 n，树高为 log₂n；
• 所以总复杂度为 O(n log n)。

2. 快速排序

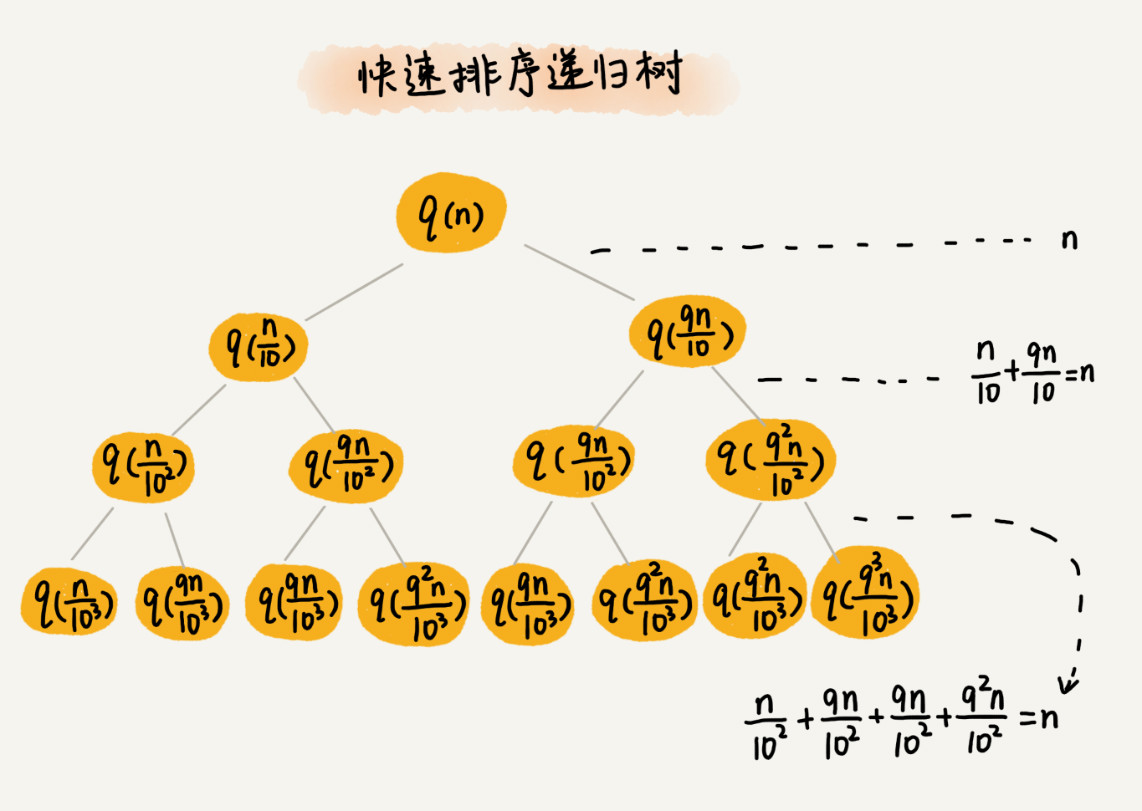
• 快速排序的过程中，每次分区都要遍历待分区区间的所有数据，所以，每一层分区操作所遍历的数据的个数之和就是 n。
• 快速排序结束的条件就是待排序的小区间，大小为 1，也就是说叶子节点里的数据规模是 1。从根节点 n到叶子节点 1，递归树中最短的一个路径每次都乘以 1/10，最长的一个路径每次都乘以 9/10。通过计算，我们可以得到，从根节点到叶子节点的最短路径是 log10n，最长的路径是 log10/9n。
• 遍历数据的个数总和就介于 nlog10n 和 nlog10/9n 之间。根据复杂度的大 O 表示法，对数复杂度的底数不管是多少，我们统一写成 log⁡n，所以，无论分区大小比例是 1:9还是1：99，999 时，快速排序的时间复杂度仍然是 O(nlogn)。

3. 斐波那契数列

递归一节中跨台阶的例子。

• 每次递归生成两个子问题，递归树呈指数增长；
• 每次分解之后的合并操作只需要一次加法运算，把这次加法运算的时间消耗记作 1。所以，从上往下，第一层的总时间消耗是 1，第二层的总时间消耗是 2，第三层的总时间消耗就是 22。依次类推，第 k层的时间消耗就是 2k−1。
• 最大树高约为n，最短路径约为n/2；
• 总体复杂度介于 O(2ⁿ) 和 O(2ⁿᐟ²) 之间，属于指数级。