内事不决问张昭，外事不决问周瑜，“ 排序 ”不决问威少_张昭 处理外事

最新推荐文章于 2024-05-20 10:24:40 发布
最新推荐文章于 2024-05-20 10:24:40 发布
阅读量277 收藏 7
点赞数 3
分类专栏： 2024年程序员学习 文章标签： java 开发语言
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2301_82241698/article/details/137896828
版权

先自我介绍一下，小编浙江大学毕业，去过华为、字节跳动等大厂，目前阿里P7

深知大多数程序员，想要提升技能，往往是自己摸索成长，但自己不成体系的自学效果低效又漫长，而且极易碰到天花板技术停滞不前！

因此收集整理了一份《2024年最新大数据全套学习资料》，初衷也很简单，就是希望能够帮助到想自学提升又不知道该从何学起的朋友。
img
img
img
img
img

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上大数据知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

如果你需要这些资料，可以添加V获取：vip204888 （备注大数据）
img

正文

}

//堆排序
public static void heapSort(int[] array){
creayHeap(array);
int end = array.length-1;
while(end > 0){
int temp = array[0];
array[0] = array[end];
array[end] = temp;
end–;
adjustDown(array,0,end);
}
}


用Java类建一个堆，好写，不过md这个时间复杂度比较高

//调用一个堆
public static void heapSort(int[] array){
PriorityQueue minHeap = new PriorityQueue<>();
for (int i = 0; i < array.length; i++) {
minHeap.offer(array[i]);
}
int i = 0;
while(!minHeap.isEmpty()){
array[i] = minHeap.poll();
i++;
}
}


## 六、快速排序


**中心思想：Partition和分治**


* 从待排序区间里选一个数，作为基准值（pivot）
* Partition：遍历整个区间，将比基准值小的放到基准值的左边，将比基准值大的放到基准值的右边
* **分治思想**，对左右两个小区间按照同样的方式处理，知道小区间的长度为1，代表已经有序；或小区间的长度为0，代表没有数据


### Partition


#### 挖坑法实现Partition


**中心思想：右填左坑，左填右坑**  
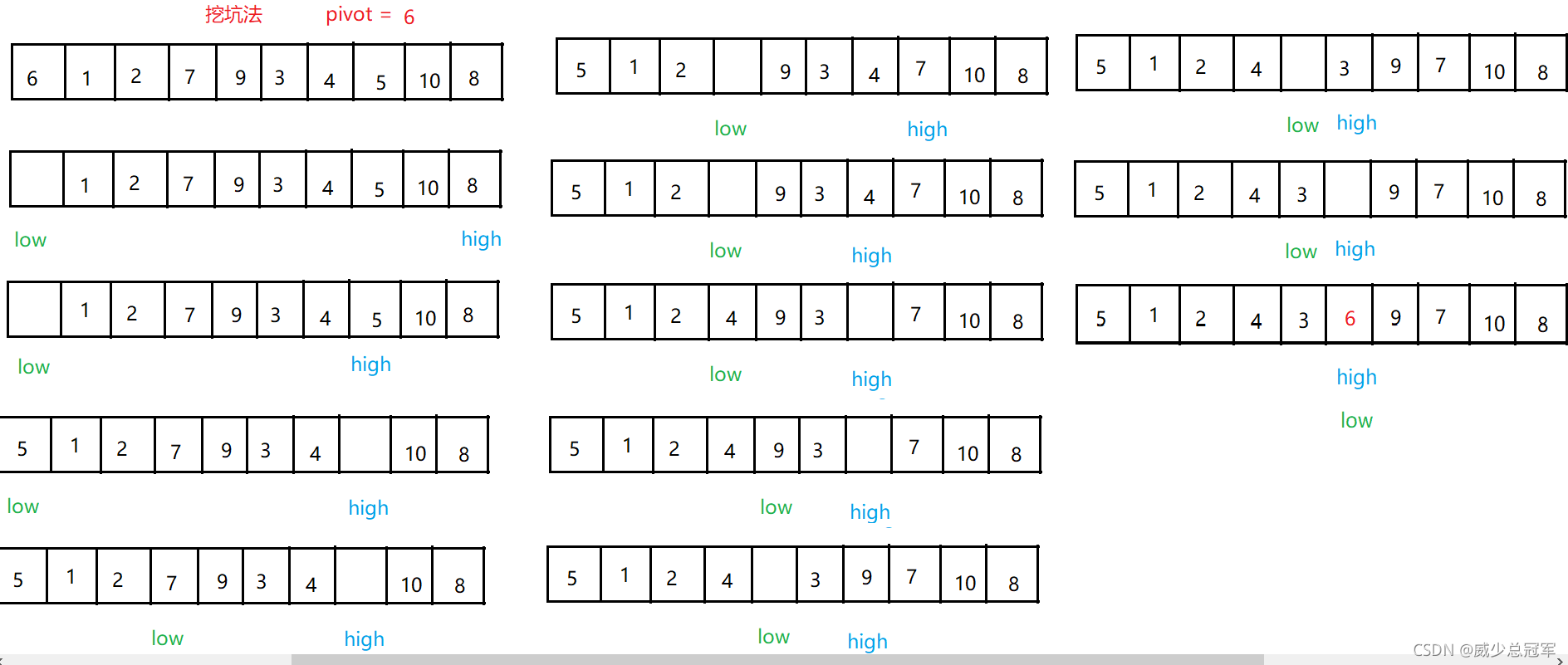
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/19d7df77ec474605a51a7755d065296f.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5aiB5bCR5oC75Yag5Yab,size_20,color_FFFFFF,t_70,g_se,x_16)


* 找一个元素作为基准（pivot）（此处是第一个元素作基准）
* low下标从左边开始遍历，high下标从右边开始遍历，low和high就是“坑”
* 首先low下标作为“坑”，需要比 pivot 小的元素填坑，high–，找到比pivot 小的元素，赋值给low
* 然后high下标作为“坑”，需要比pivot 大的元素填坑，low++，找到比pivot 大的元素，赋值给high
* 当low和high相遇时，此下标指向的元素就是 pivot
* 一次Patition结束，此时low/high的左边是比pivot小的元素，low/high右边是比pivot大的元素
* 返回pivot的下标（low/high），作为下一次Patition的区间

public static int Partition(int[] array, int low, int high){
int pivot = array[low];
while(low < high){
//注意这两个循环的顺序，如果是先low后high，第一个坑没法填，最后一个数白白丧失
//注意可以是 >=和<=，或 >=和<，或 >和<=
//不能是< 和 > , 相等的也交换，死循环
while(low < high && array[high] >= pivot){
high–;
}
array[low] = array[high];
while(low < high && array[low] <= pivot){
low++;
}
array[high] = array[low];
}
array[low] = pivot;
return low;
}


#### Hoare法实现Partition


**中心思想：左右交换**  
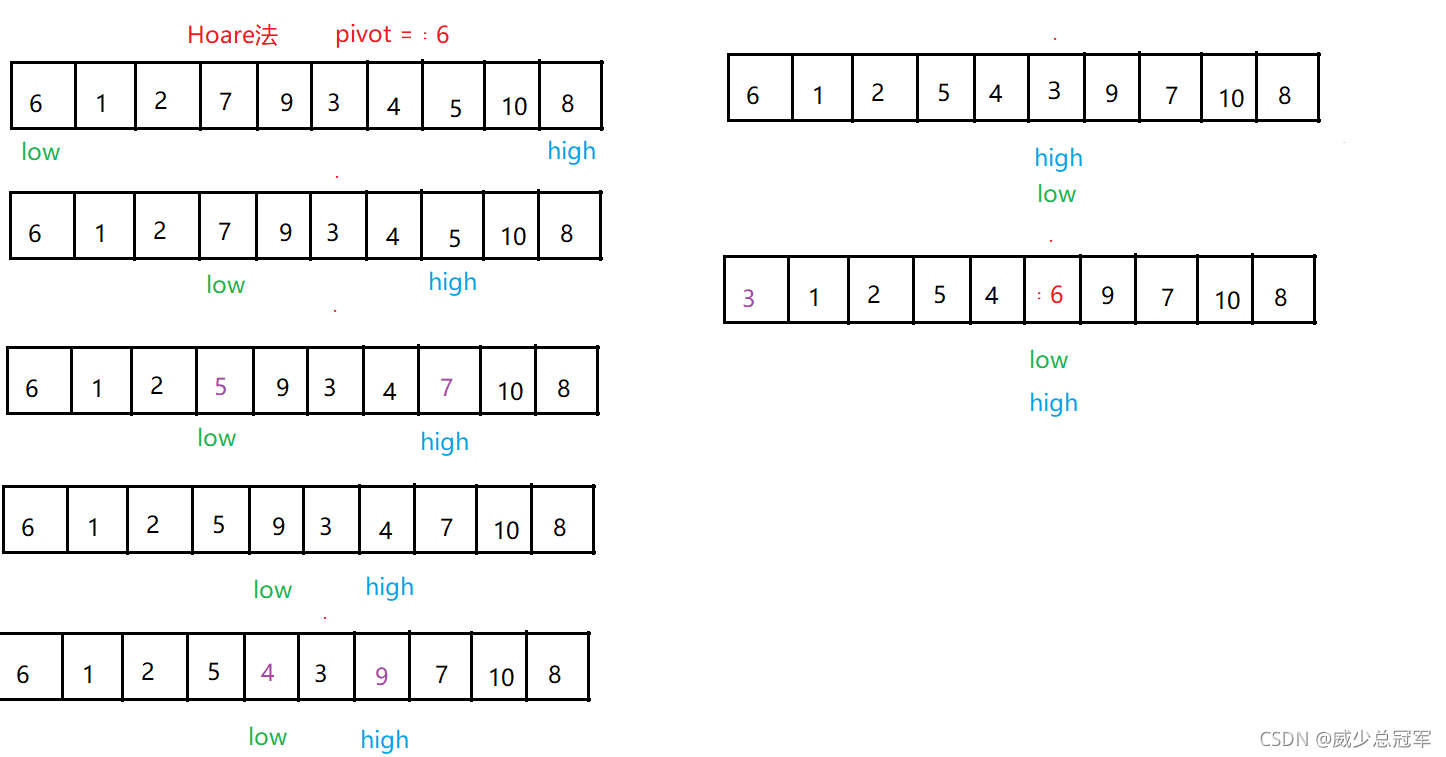
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/b93a28bc88f14a8eaa4e44bb421438ab.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5aiB5bCR5oC75Yag5Yab,size_20,color_FFFFFF,t_70,g_se,x_16)


* 找一个元素作为基准（pivot）（此处是第一个元素作基准）
* high从右边开始遍历，left从左边开始遍历
* high找到比 pivot 小的元素，low找到比 pivot 大的元素，交换元素
* high与left相遇时，此下标指向的元素 小于pivot ，与 区间起点 的元素交换
* 返回pivot的下标（low/high），作为下一次Patition的区间




public static void Swap(int[] array, int i, int j){
    int temp = array[i];
    array[i] = array[j];
    array[j] = temp;
}
public static int Hoare(int[] array, int low, int high){
    int start = low;
    int pivot = array[low];
    while(low < high){
//注意顺序，先后再前，让high去找low，两者相遇的地方是比temp小的数
//同样可以是>=和<= 或 >和<= 或 >=和<
//如果是>,< 会死循环的
        while(low < high && array[high] >= pivot){
            high--;
        }
        while(low < high && array[low] <= pivot){
            low++;
        }
        Swap(array,low,high);
    }
    Swap(array,low,start);
    return low;
}


### 递归分治


* 通过递归的方式对左右两个小区间再进行快速排序，直到区间长度为1时，递归结束




public static void quickSort(int[] array, int start, int end){
    if(start >= end){
        return;
    }
    int pivot = Partition(array,start,end);

    quickSort(array,start,pivot-1);
    quickSort(array,pivot+1,end);
}
//这一步没JB用，就保持下统一性而已
public static void quickSort(int[] array){
    quickSort(array,0,array.length-1);
}


#### 时间空间复杂度


**稳定性：不稳定**  
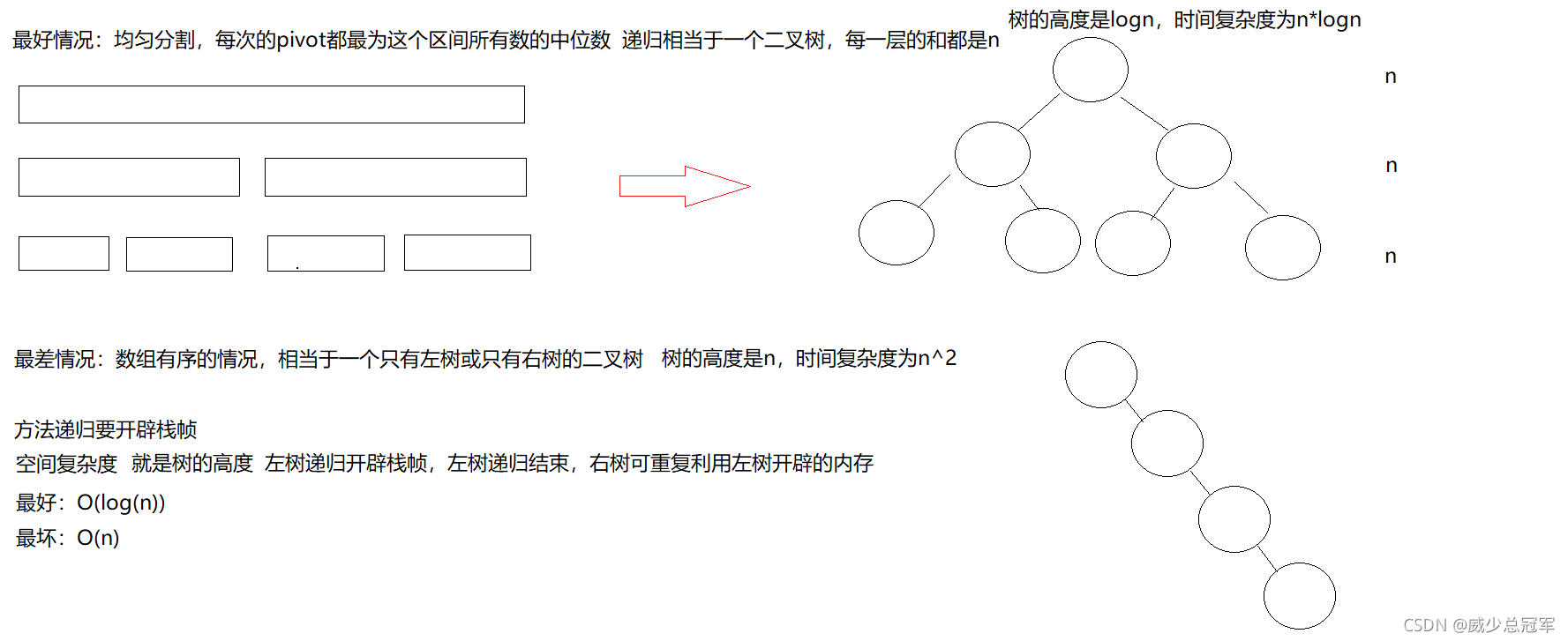
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/ad12e04eb86842bc813811aee702f6a9.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5aiB5bCR5oC75Yag5Yab,size_20,color_FFFFFF,t_70,g_se,x_16)  
 **最坏情况时，可能会出现栈溢出的情况**  
 所以可以通过基准值的选择进行优化


### 优化


1. **基准值的选择**


* 选择边上（low或者high）
* 随机选择，可以将随机下标的值与low下标的值互换
* 三数取中，要求 array[mid] <= array[low] <= array[high]


2. 待排序区间小于一个阈值时，使用直接插入排序


#### 三数取中


**还是array[low] 作基准(pivot)  
 三数取中  
 让array[mid] <= array[low] <= array[high]**  
 可以确定其中最大/最小数的位置，在比较其余两个数

//元素交换
public static void Swap(int[] array, int i, int j){
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
//array[mid] <= array[low] <= array[high]
//很多种方法，不一一列举了
public static void ThreeMiddle(int[] array,int low, int high){
int mid = (low+high)/2;
if(array[low] < array[mid]){
Swap(array,low,mid);
}
if(array[high] < array[low]){
Swap(array,low,high);
}
if(array[low] < array[mid]){
Swap(array,low,mid);
}
}


### 非递归分治


**中心思想：区间边界放栈中，怕甚(Partition)一次取两个**  
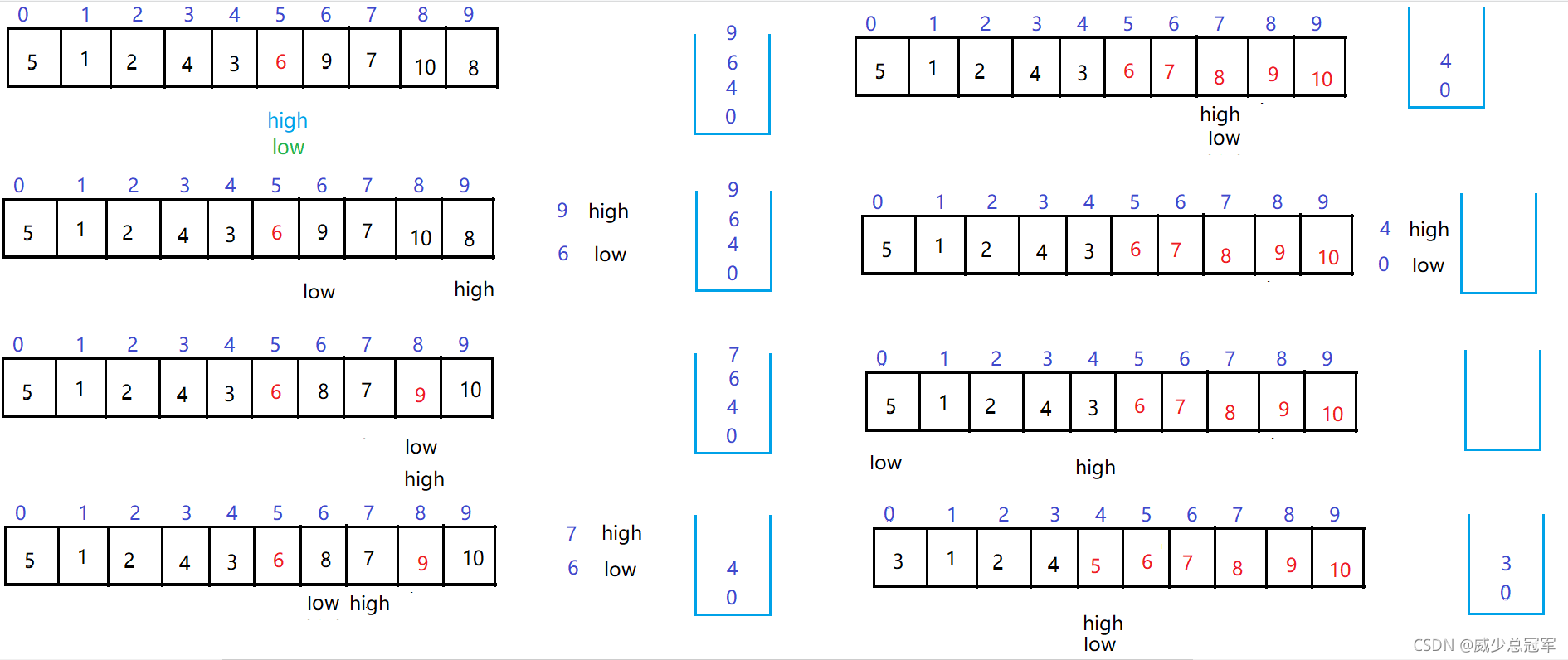
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/a14964cd57cc4a738536ee65220a9634.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5aiB5bCR5oC75Yag5Yab,size_20,color_FFFFFF,t_70,g_se,x_16)


* 调用Partition后，找到pivot
* 把当前pivot的**左区间和右区间的边界下标**放到栈中，当这个区间至少有两个元素的时候，才入栈；若只有一个元素，说明有序了，不再入栈
* 判断栈是否为空，如果不为空的话，弹出栈顶的**两个元素**，放的顺序决定第一个元素给low还是给high
* 再进行Partition




public static void quickSort2(int[] array){
    if(array.length == 0){
        return;
    }
    Stack<Integer> stack = new Stack<>();
    stack.push(0);
    stack.push(array.length-1);
    while(!stack.isEmpty()){
        int high = stack.pop();
        int low = stack.pop();
        int pivot = Partition(array,low,high);
        if(pivot > low+1) {
            stack.push(low);
            stack.push(pivot - 1);
        }
        if(pivot < high-1) {
            stack.push(pivot + 1);
            stack.push(high);
        }
    }
}


## 七、归并排序


**中心思想:** **合并两个有序“数组”**  
 先将已有的序列分解成较短的子序列，使每个子序列有序，再将已经有序的子序列合并，得到完全有序的序列，即**分解与合并**  
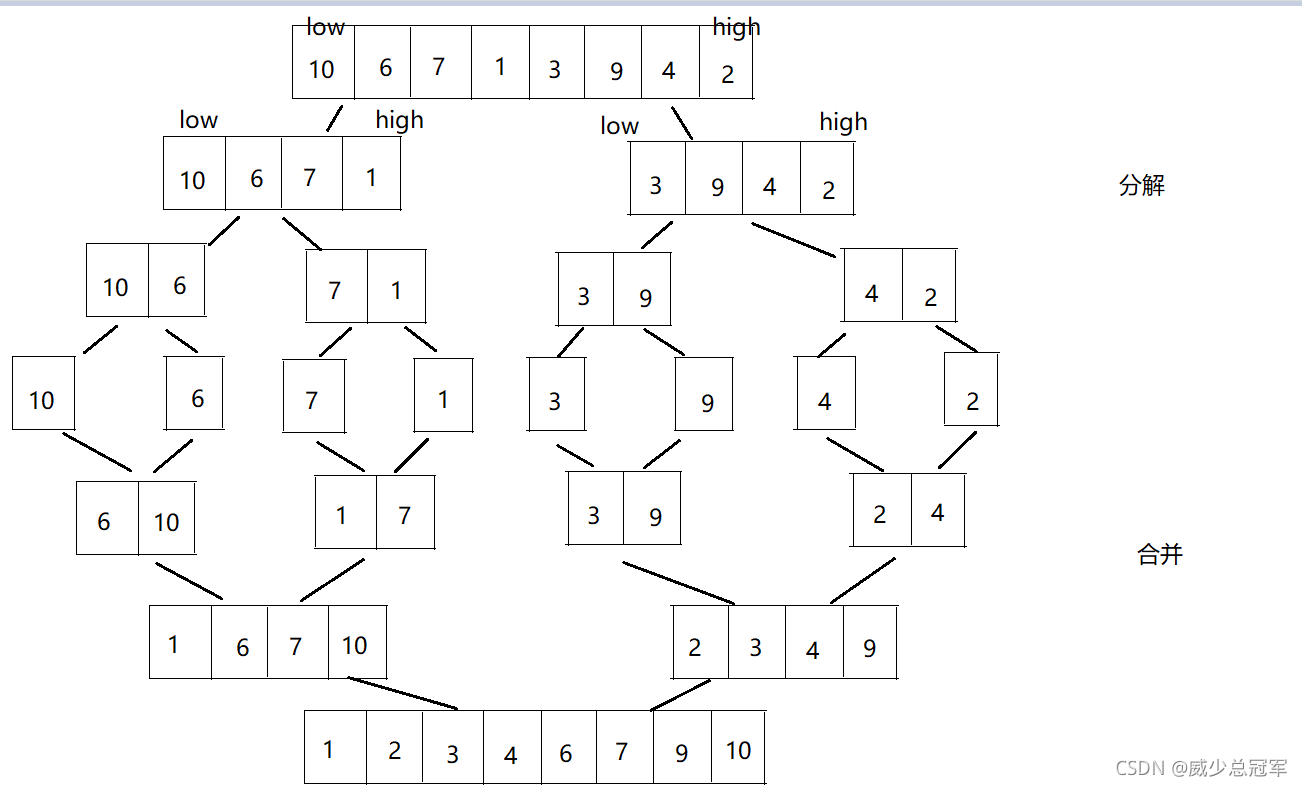
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/088f5386a8dc4309a825e1b462a7b9ef.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5aiB5bCR5oC75Yag5Yab,size_20,color_FFFFFF,t_70,g_se,x_16)


### 归并排序（递归）


![在这里插入图片描述](https://img-blog.csdnimg.cn/1d6ee65977c14d3387c11b3c73acc21a.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5aiB5bCR5oC75Yag5Yab,size_20,color_FFFFFF,t_70,g_se,x_16)


* 将数组通过递归分解，直到low=high时（即只有一个元素的时候），递归结束
* 利用递归改变left和right，将新的 [ left，mid ] 看作一个数组，将 [ mid+1，right ] 看作一个数组，**将两个有序数组 合并成 一个有序数组**

public static void merge(int[] array, int low, int mid, int high){
int[] temp = new int[high-low+1];
int k = 0;
int s1 = low;
int e1 = mid;
int s2 = mid+1;
int e2 = high;
while(s1 <= e1 && s2 <= e2){
while(s1 <= e1 && array[s1] <= array[s2]){
temp[k++] = array[s1++];
}
while(s2 <= e2 && array[s2] <= array[s1]){
temp[k++] = array[s2++];
}
}
while(s1 <= e1){
temp[k++] = array[s1++];
}
while(s2 <= e2){
temp[k++] = array[s2++];
}
for (int i = 0; i < temp.length; i++) {
array[i+low] = temp[i];
}
}
public static void mergeSort(int[] array, int low, int high){
if(low == high){
return;
}
int mid = (low+high)/2;
mergeSort(array,low,mid);
mergeSort(array,mid+1,high);
merge(array, low, mid, high);
}

public static void mergeSort(int[] array){
    mergeSort(array,0,array.length-1);
}


### 非递归的归并排序


* 通过gap控制需要合并的两个序列的长度，1–>2–>4–>8
* 在gap的一次循环中，s1、e1、s2、e2遍历所有的序列，合并两个有序的序列
* 可能序列正好匹配 可能只剩下一段序列（没有与之合并的第二段序列）；如果剩下无法合并的序列，不做改变

public static void merge(int[] array, int gap){
int[] temp = new int[array.length];
int k = 0;
int s1 = 0;
int e1 = s1+gap-1;
int s2 = e1+1;
int e2 = s2+gap-1 > array.length-1 ? array.length-1 : s2+gap-1;
//有两段
while(s2 < array.length) {
while (s1 <= e1 && s2 <= e2) {
while (s1 <= e1 && array[s1] <= array[s2]) {
temp[k++] = array[s1++];
}
while (s2 <= e2 && array[s2] <= array[s1]) {
temp[k++] = array[s2++];
}
}
while(s1 <= e1) {
temp[k++] = array[s1++];
}
while(s2 <= e2){
temp[k++] = array[s2++];
}
s1 = e2+1;
e1 = s1+gap-1;
s2 = e1+1;
e2 = s2+gap-1 > array.length-1 ? array.length-1 : s2+gap-1;
}
//只有一段了
while(s1 < array.length && s1 <= e1){
temp[k++] = array[s1++];
}

    for (int i = 0; i < temp.length; i++) {
        array[i] = temp[i];
    }
}
public static void mergeSort2(int[] array){
    for (int gap = 1; gap < array.length; gap\*=2) {
        merge(array,gap);
    }
}


## 时间复杂度与空间复杂度


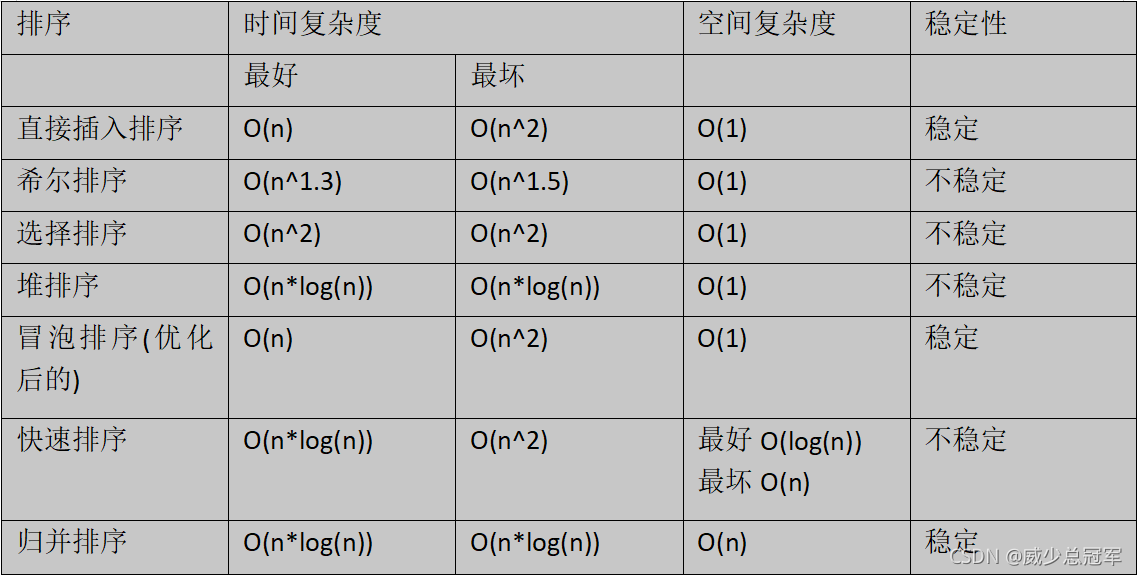
![在这里插入图片描述](https://img-blog.csdnimg.cn/e39bdadb89984e259ab3151e78fc5a47.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5aiB5bCR5oC75Yag5Yab,size_20,color_FFFFFF,t_70,g_se,x_16)


### 计算运行时间的小妙招




    long begin = System.currentTimeMillis();
    insertSort(array);
    long end = System.currentTimeMillis();
    System.out.println(end - begin);



**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**需要这份系统化的资料的朋友，可以添加V获取：vip204888 （备注大数据）**
![img](https://img-blog.csdnimg.cn/img_convert/cd0538651dfa0a7eceaeb469611eb863.png)

**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**

stem.currentTimeMillis();
        insertSort(array);
        long end = System.currentTimeMillis();
        System.out.println(end - begin);

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化的资料的朋友，可以添加V获取：vip204888 （备注大数据）
[外链图片转存中…(img-rp6voyC6-1713377969634)]

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

2301_82241698
关注
  • 3
    点赞
  • 踩
  • 7
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
论文研究-Tunable single-longitudinal-mode erbium-doped fiber laser employing a two-taper Mach-Zehnder interferometer filter and saturable absorber.pdf
08-16
基于双锥型马赫增德尔干涉仪和可饱和吸收体的可调谐单纵模掺铒光纤激光器，张昭，曹志刚，本文提出了一种可调谐单纵模掺铒光纤激光器，其输出激光线宽1.4kHz。激光器使用一个双锥型马赫增德尔干涉仪作为波长选择装置...
论文研究-高校贫困生管理的信息解决方案 .pdf
08-16
高校贫困生管理的信息解决方案，张昭，，本文针对目前高校贫困生管理工作的现状和存在的难题，设计了基于C/S模式的贫困生信息管理系统，并给出了贫困生认定的信息解决方案
jar包增量更新分析
junlaiyan的专栏
05-16 244
借助jdeps分析出jar包的增量文件
java实现拼图小游戏
monkey108的博客
05-16 608
本文主要提供用java实现的拼图小游戏源代码。
c【语言】了解指针，爱上指针（1）
yzqy_的博客
05-16 892
在计算机中，数据是存储在内存中的，cpu从内存中读取数据，为了方便读取数据，内存又被划分为了一个个的内存单元，一个内存单元的大小就是一字节，一字节等于8bit位，我们给内存进行编号，这个编号就是地址，在c语言中给这个地址起了个名字。是的，亲爱的读者你肯定发现了，&a、p和pc输出的地址是一样的,但&a+1与p+1输出的地址是一样的00EFF940，一次都跳过了4字节，而pc+1输出的却是00EFF93D，一次只跳过一个字节。但是硬件与硬件之间是相互独立的，这该如何实现数据传输呢？”答案当然是否定的。
命令执行漏洞（二）
XLbb的博客
05-15 895
POST方法，S2-045-bypass-2漏洞存在！,程序更改为S2-045-bypass-2漏洞测试模式, 响应码: 200。POST方法，S2-046-bypass漏洞存在！POST方法，S2-045-bypass漏洞存在！POST方法，S2-046-1漏洞存在！POST方法，S2-046-2漏洞存在！POST方法，S2-046-3漏洞存在！POST方法，S2-045-1漏洞存在！POST方法，S2-045-3漏洞存在！POST方法，S2-045-2漏洞存在！POST方法，S2-045-4漏洞存在！
java数据结构与算法(验证二叉搜索树)
磐门的博客
05-17 241
节点返回空为ture,节点的值不在对应数据大小范围内返回false。将验证二叉搜索树计算同样可以转换为相同子问题，所以比较适合用递归。node为root的左节点时，max更新为root.val。node为root的右节点时，min更新为root.val。
Kubernetes 审计日志采集与分析最佳实践
观测云的博客
05-17 1015
​Kubernetes 在 1.7 版本中发布了审计（Audit）日志功能，通过审计日志，我们能够非常清晰的知道 K8S 集群到底发生了什么事情。
java导出excel动态加载多sheet多复杂表头
weixin_43931108的博客
05-14 242
java导出excel动态加载多sheet多复杂表头
Android Model引入其他aar包 导致无法打包成aar
qq_27400335的博客
05-16 340
Android Model引入其他aar包 导致无法打包成aar
SpringBoot事件发布与监听，观察者模式使用
小哇
05-16 213
可以发现，用户注册与信息推送强耦合，用户注册其实到存库成功，就已经算是完成了，后面的信息推送都是额外的操作，甚至信息推送失败报错，还会影响API接口的结果，如果在同一事务，报错信息不捕获，还会导致事务回滚，存库失败。本文记录springboot使用@EventListener监听事件、ApplicationEventPublisher.publishEvent发布事件实现业务解耦。
Solon 的 InjectGather 在 AppContext 里起到了什么作用？
最新发布
Itmastergo的博客
05-20 364
Solon是一款轻量级的Java开发框架，其设计理念简单且易于使用，主要应用于微服务和现代化的Java应用开发。Solon框架的核心目标是提供一个高效且简洁的开发环境，使开发者能够快速构建和部署应用程序。在Solon框架中，AppContext是核心上下文，它管理着整个应用程序的生命周期，包括bean的注册、依赖注入、事件管理等。AppContext是一个应用程序的核心容器，类似于Spring中的。Bean管理：负责注册和管理应用程序中的所有bean。依赖注入：提供自动化的依赖注入机制。事件管理。
Java基础——字符串
Kenard的博客
05-17 935
基本数据类型、包装类 转成字符串，调用String类的public String valueOf(int n)可将int型转换为字符串相应的valueOf(byte b)、valueOf(long l)、valueOf(float f)、valueOf(doubled)、valueOf(boolean b)可由参数的相应类型到字符串的转换。下面示例中，s1 和 s2 采用 new String() 的方式新建了两个不同字符串，而 s3 和 s4 是通过 s1.intern() 方法取得一个字符串引用。
初识Spring Cloud
u011627218的专栏
05-20 482
一、介绍。
【C++11】std::async函数介绍及问题梳理
朝花夕拾
05-14 1020
本文介绍了C++标准库中的 std::async 函数，该函数用于启动异步任务，提高程序的并发性能。我们首先讨论了 std::async 的基本用法和参数选项，包括异步执行策略、返回值类型和传递参数的方式。接着，探讨了 std::async 可能存在的一些问题，如异常处理、线程资源管理和潜在的性能影响。最后，提出了一些使用 std::async 时需要注意的关键点，以确保代码的可靠性和性能。
Java的数据类型
yican2580的博客
05-15 559
本章详细讲解了Java中的变量和类型，有一些与C语言有区分，并讲解了字符串和数字如何相互转换。
Java-异常
sgliquangang的专栏
05-20 113
会执行，会在return前执行，这个关键字的逻辑就是这么设计的，只要程序正常执行到了try，那就一定会执行。catch和finally可以省略其一，另一个不能被省略。
mqtt异常导致程序崩溃终止
xiyafei122的博客
05-16 133
原因：myMQTTClient.connect();会一直new client，导致之前的 连接断开，从而导致死循环。1、springboot集成mqtt超级详细步骤。
《三国演义》是中国四大名著之一，该书描述了100多个典型人物。统计书中典型人物名字出现的次数能够侧面反映人物的重要性。请给出这个计算问题的IPO描述，重点描述其中的算法部分。出程序。
03-22
处理：统计每个典型人物名字在文本中出现的次数 输出：每个典型人物名字在文本中出现的次数，按照出现次数从高到低排序 算法部分： 1. 读取《三国演义》文本文件，将其转化为字符串。 2. 定义一个字典，用于存储...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值