三角函数积分(一)万能公式法在上一节中,用万能公式法解题三角函数,但是虽然方法比较万能,但是在一些题目中解题会比较繁琐,所以学习更多的三角函数积分的解法是非常有必要的。
这一节,主要练习“缩分母”技巧。
当分母为 1+cosx或者1+sinx 时,使用缩分母技巧,将两项变为一项,会降低题目的难度。因为我们宁愿让分子有很多项,也不想让分母有很多项,因为分母有很多项时,我们可以将其拆开,拆成若干个不定积分之和。
技巧一:使用二倍角公式。
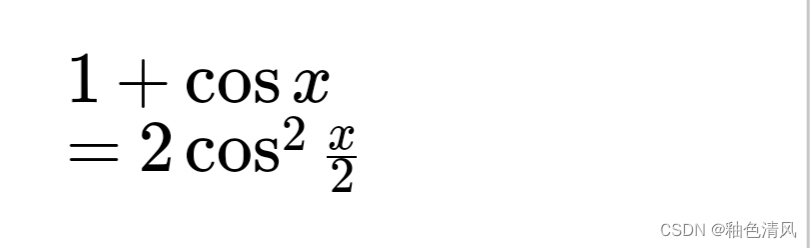
练习1:
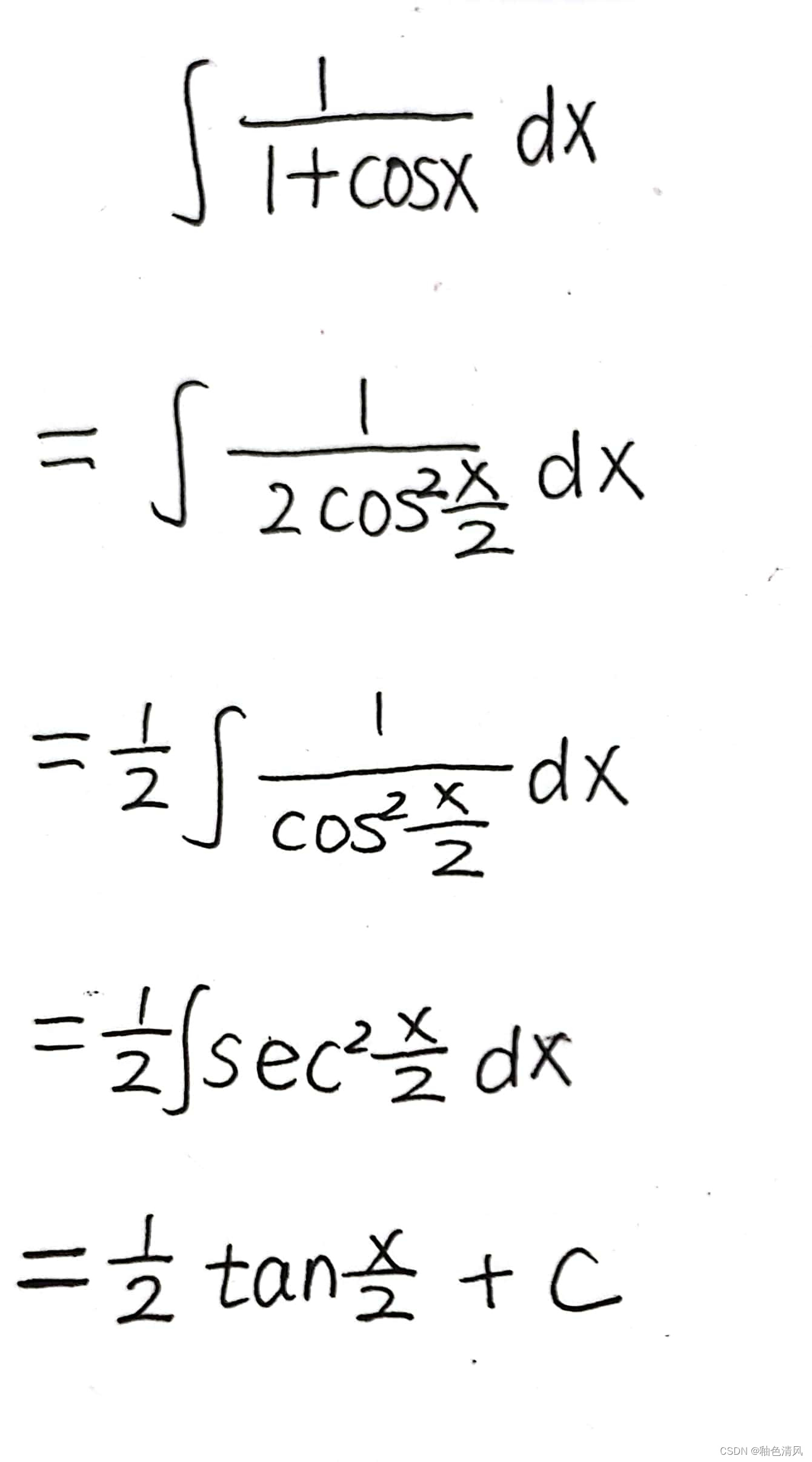
当然这道题目,它之后分母含有cos函数我,切且次数为一次,所以使用万能公式法也是很不错的选择。
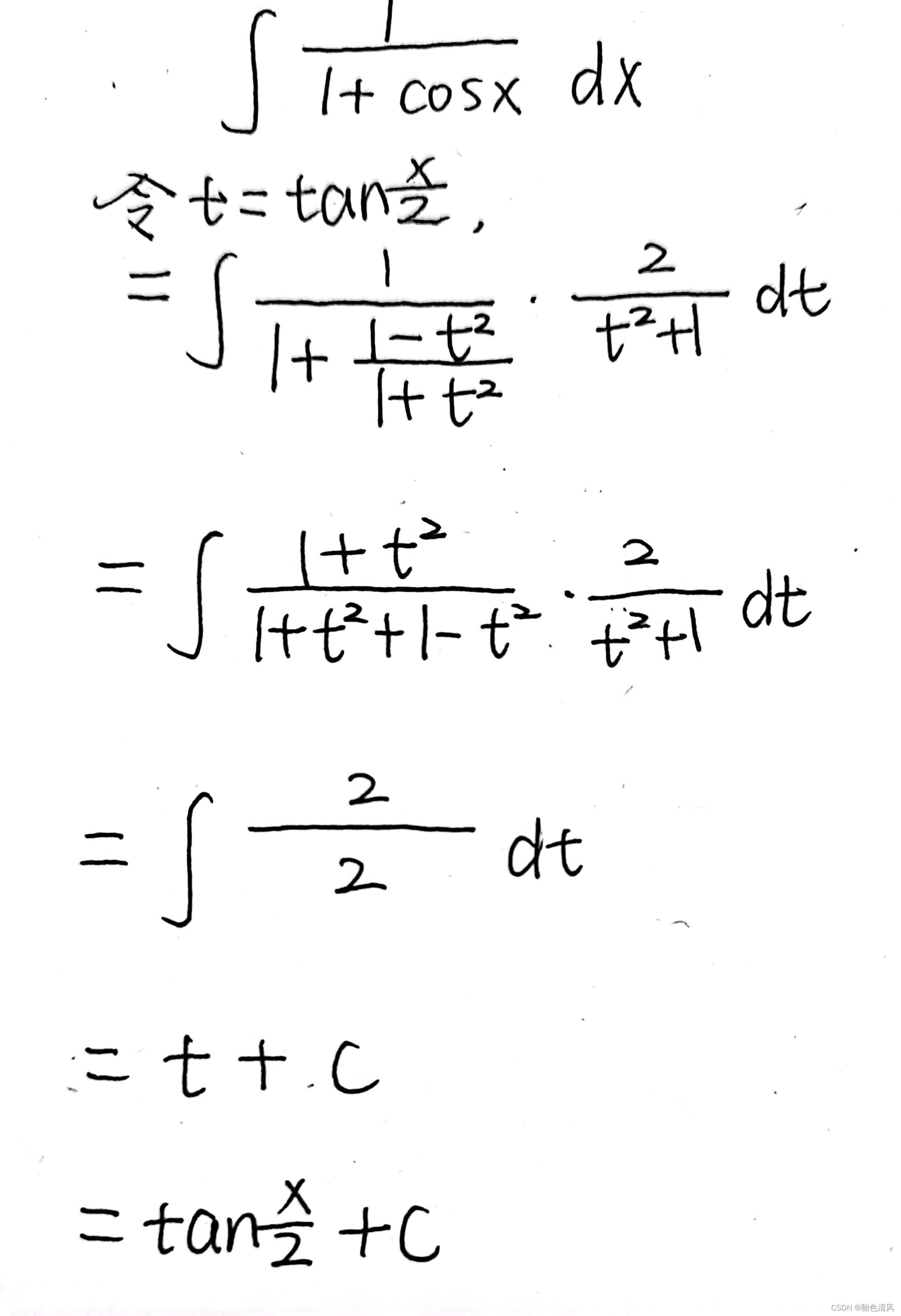
技巧二:分子分母同乘共轭表达式
分母为 1+cosx 可以分子分母同乘 1-cosx
分母为1+sinx 可以分子分母同乘1-sinx
练习2:
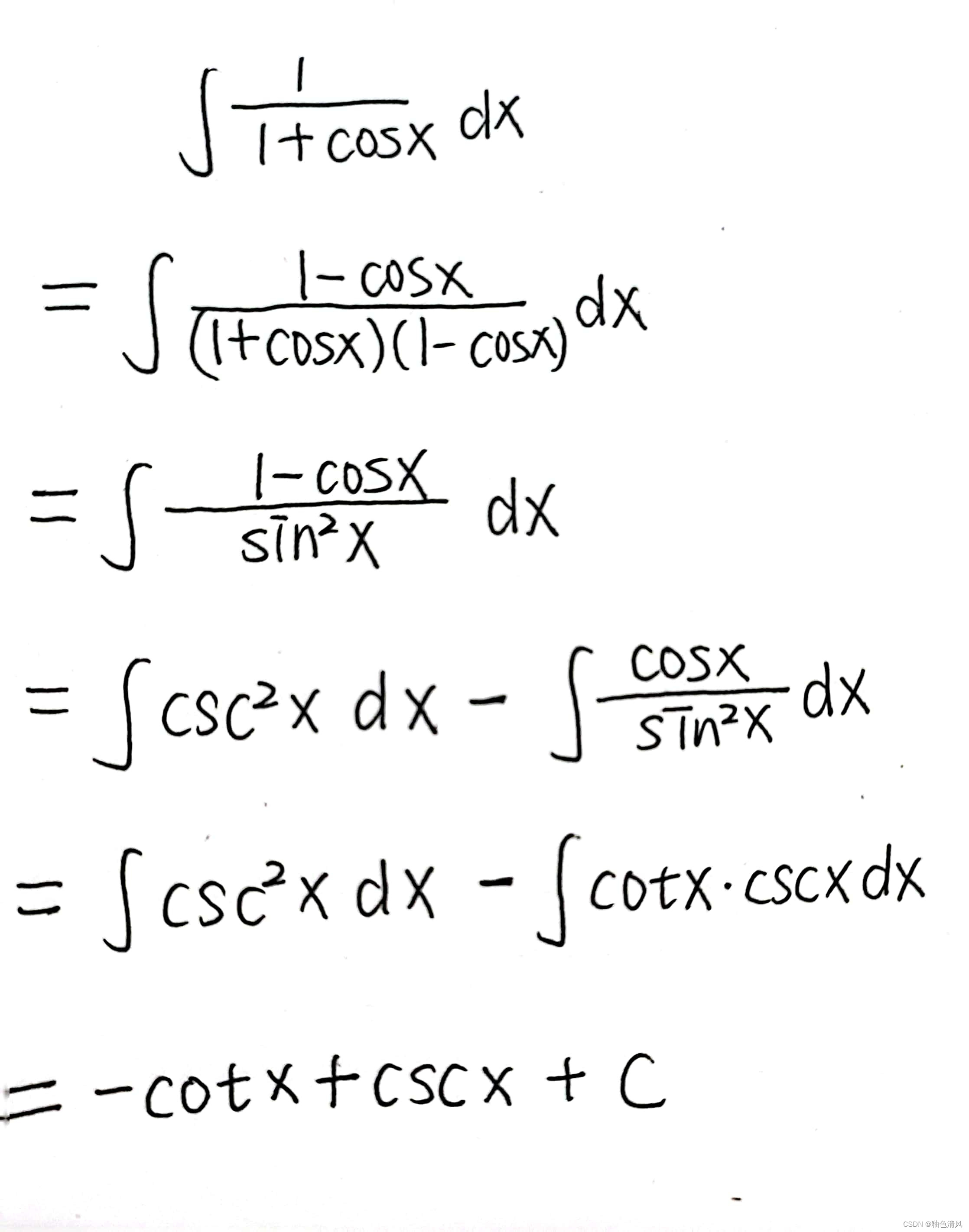
从上面,我们可知,我们深记一些三角函数的积分是十分有必要的。
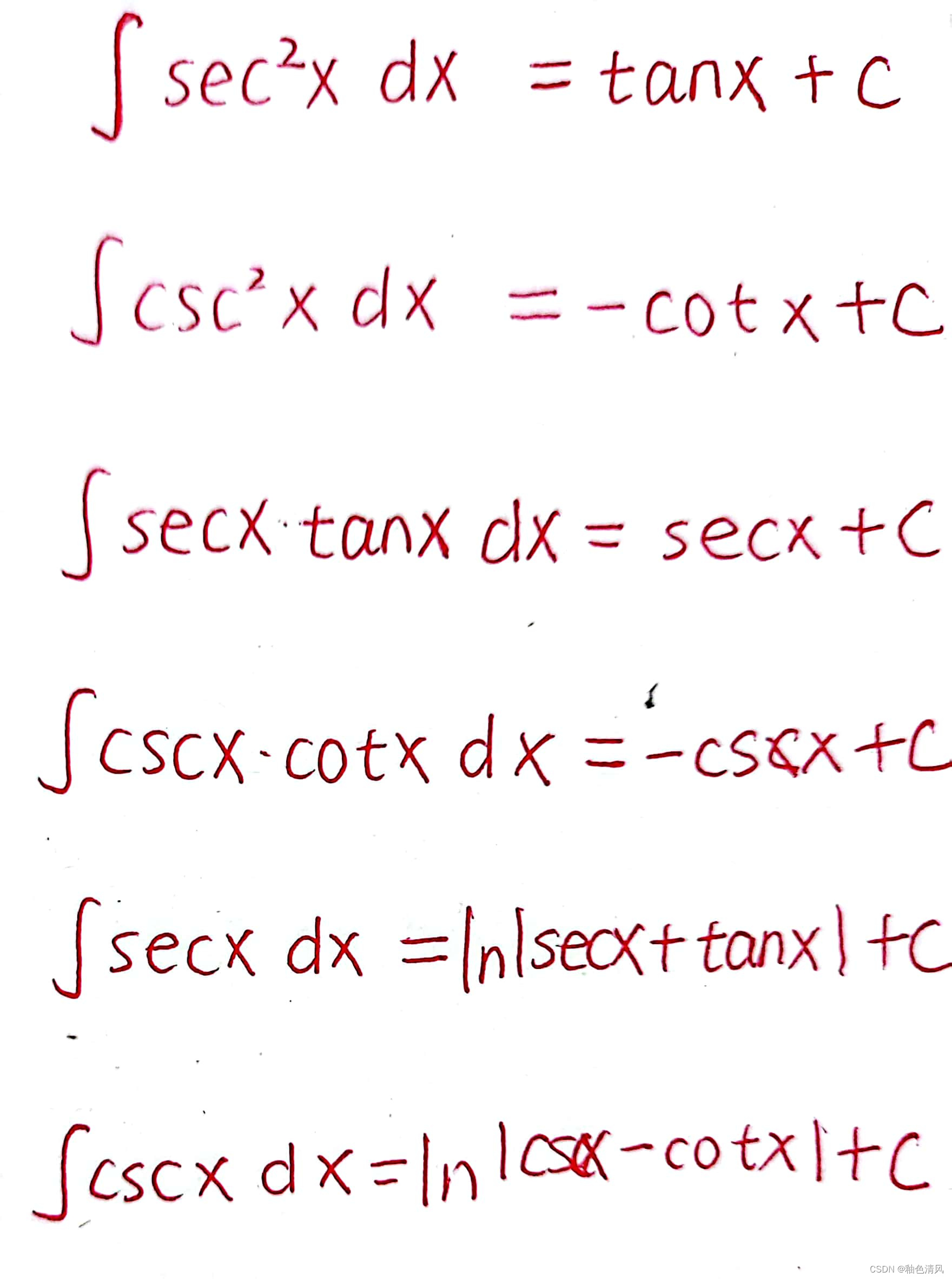
练习3:
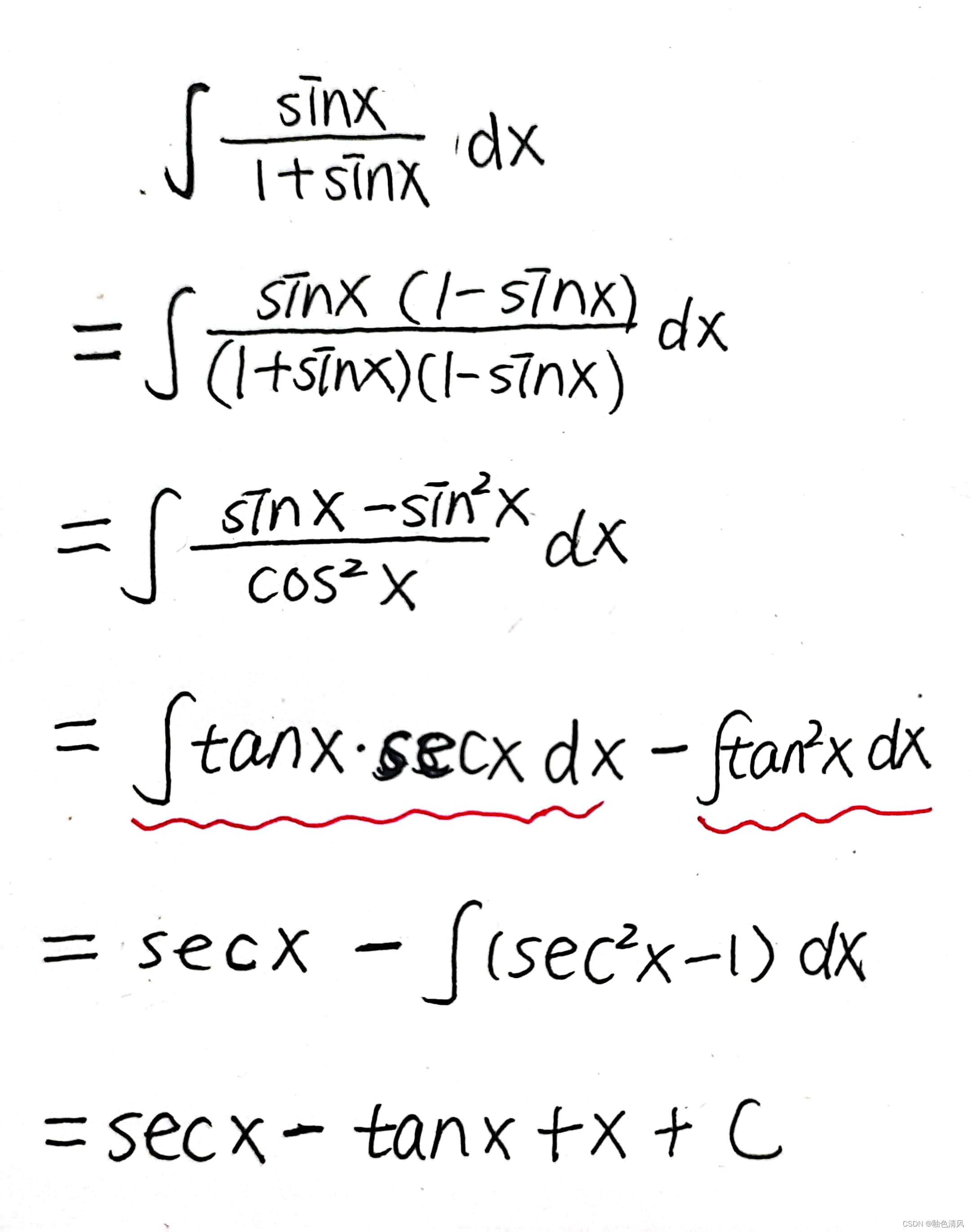
补充:
当我们遇到求tan²x时,根据tan²+1=sec²x,将其转化为求sec²x-1的积分。
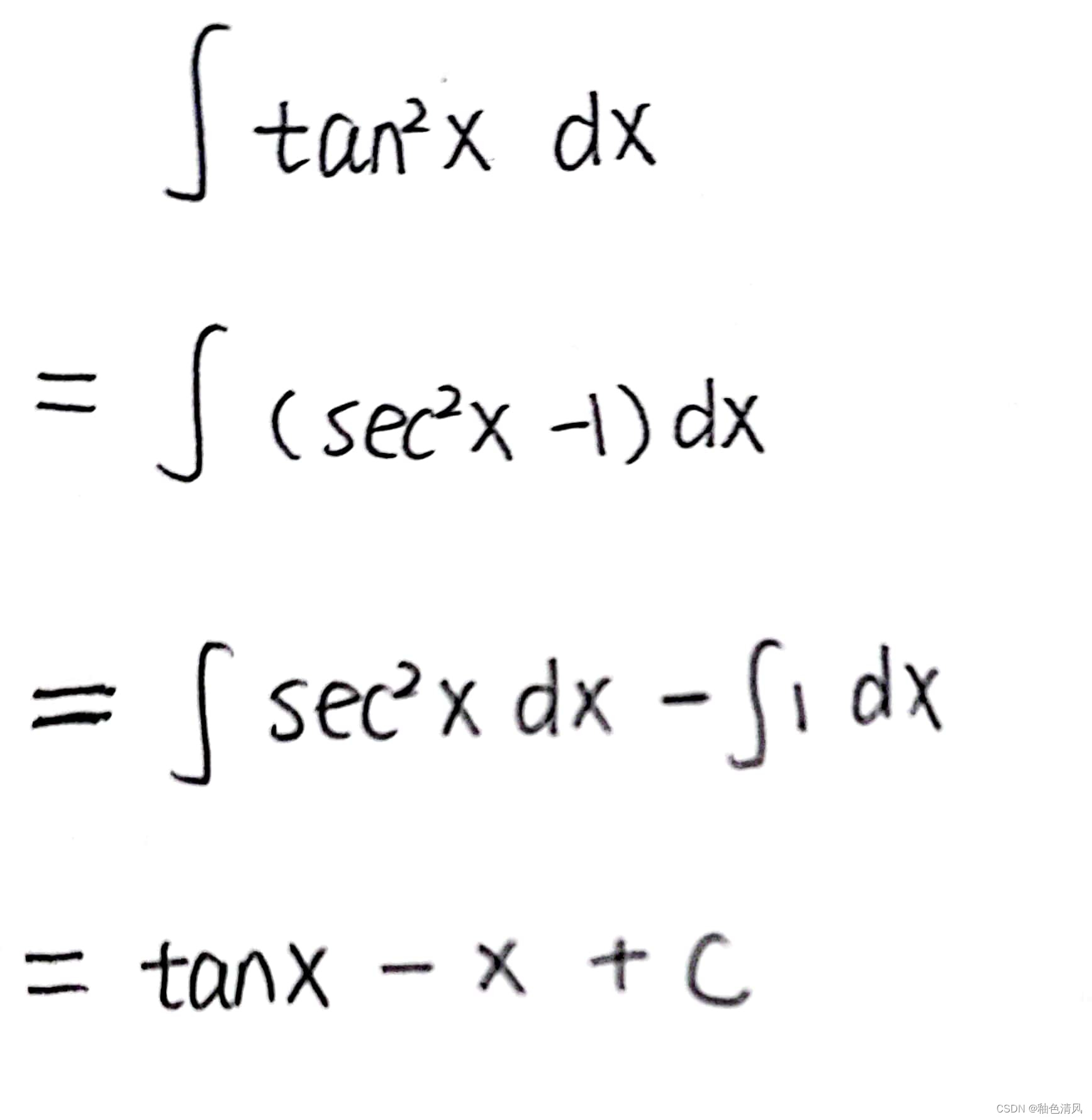
方法二:化归
sinx=cos(π/2-x)由此可以将sin函数化为cos函数。
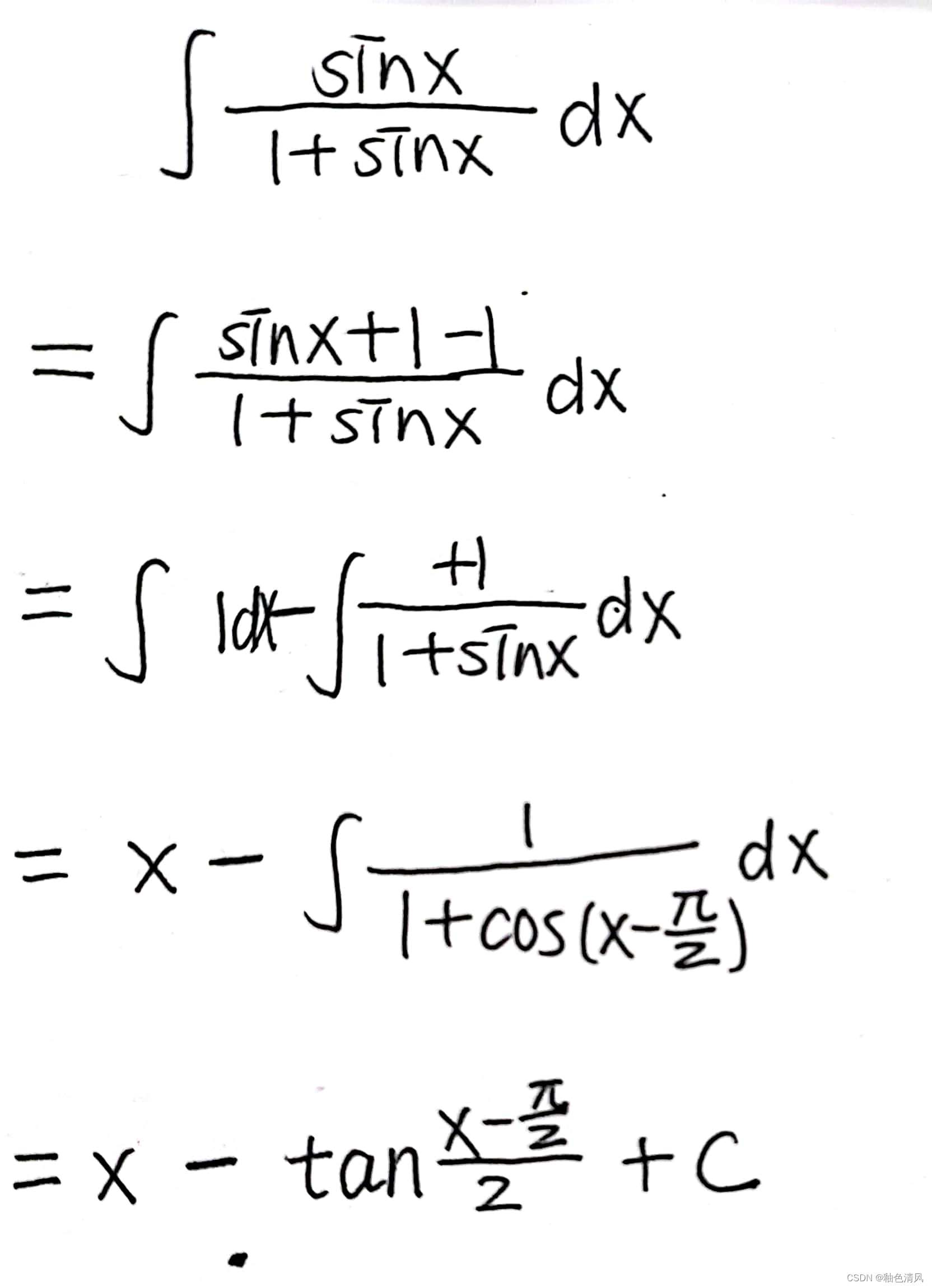
思考🤔:这个题目分子都含有一次项sinx,使用万能公式法怎么样?
不妨来尝试一下。

到最后我们转化为有理函数求积分,但是计算这个ABCD不见得很容易。
回想之前上一节用万能公式法,都是分母有三角函数且次数为一次,能够极大的利用万能公式法的优势,将其解出来。
所以这道题我们可以加项减项,降低难度。
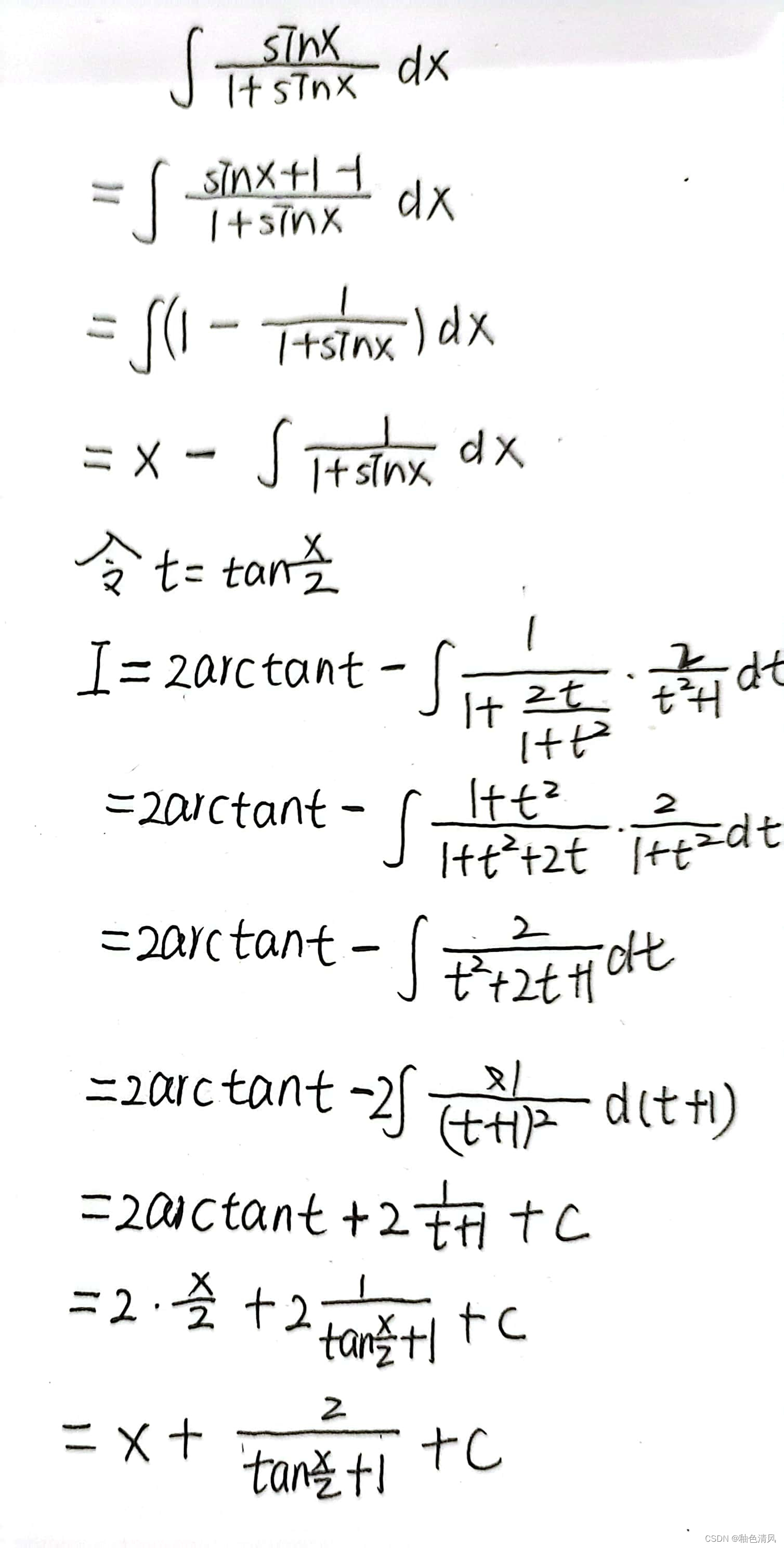
技巧三:辅助角公式-合二为一
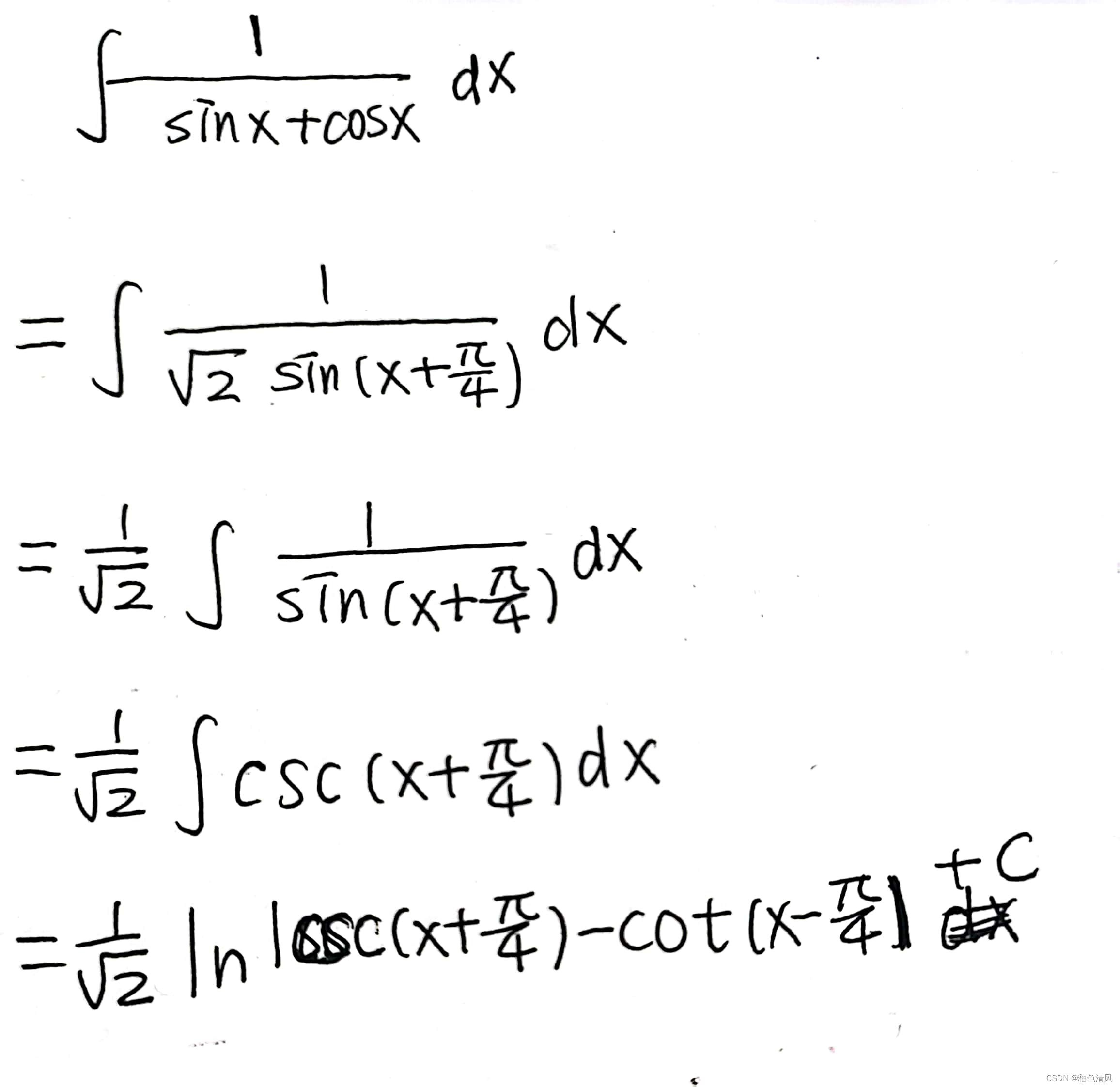








 文章介绍了在解决三角函数积分问题时,除了万能公式法外,还可以运用“缩分母”技巧,如当分母为1+cosx或1+sinx时,可以通过变形简化问题。此外,提到了二倍角公式和化归方法(如sinx=cos(π/2-x))在解决特定类型问题时的作用。同时,建议通过辅助角公式降低题目难度,并举例说明了如何运用这些技巧。
文章介绍了在解决三角函数积分问题时,除了万能公式法外,还可以运用“缩分母”技巧,如当分母为1+cosx或1+sinx时,可以通过变形简化问题。此外,提到了二倍角公式和化归方法(如sinx=cos(π/2-x))在解决特定类型问题时的作用。同时,建议通过辅助角公式降低题目难度,并举例说明了如何运用这些技巧。

















 3883
3883

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










