游戏开发必备：高效的 AABB、球体和 OBB 碰撞检测算法

最新推荐文章于 2025-04-08 16:11:31 发布

Xayla

最新推荐文章于 2025-04-08 16:11:31 发布

阅读量1.2k

点赞数 23

分类专栏：游戏开发 C++技术文章标签：算法游戏开发 AABB 碰撞检测游戏物理虚幻引擎

本文链接：https://blog.csdn.net/2302_76401343/article/details/146977616

版权

本文系VIP文章,如果你还不是VIP,请移步https://www.ilikexff.cn/articles/166免费阅读!

在游戏开发中，碰撞是一个常见且基础的术语，也是绝大部分3D游戏避不开的技术点。本文基于3D/2D游戏中物体碰撞的基本数学原理、计算实现等方面进行展开，时间关系，关于碰撞检测可能涉及到的物理部分的内容可能会在后续的维护中进行更新。

文中涉及到的三维配图均来自VisuAlgoX(已开源,好用麻烦点个star)

文中涉及的手稿均为本人亲手画的,比较抽象但是可以食用,不是美术专业,理解下吧!

基础铺垫

在正式讨论物体碰撞之前，有必要先铺垫一些相关的基础知识。这不仅能帮助我们更好地理解后续内容，特别是对于初学者来说，也能降低理解成本。

在现实世界中，物体的形状是复杂而不规则的，但在三维游戏世界中，我们所看到的每一个物体——无论是赛车、人物角色、墙壁，还是武器——实际上都是由相对规则的几何图形包裹起来的。这些几何图形被称为碰撞体（Collision Shape），它们决定了游戏引擎在进行碰撞检测时如何计算物体之间的交互。

你可能会问，为什么要使用几何图形，而不是直接采用物体本身的精确模型来进行碰撞计算呢？

原因很简单，主要是为了优化性能，减少计算量。游戏运行时，可能会有成千上万个物体相互作用，如果直接使用复杂的三角网格进行碰撞检测，计算成本将会非常高，严重影响游戏的流畅性。

因此，我们通常使用相对简单的几何形状（如矩形、立方体、球体、胶囊体等）来近似表示物体的边界，从而加快碰撞检测的计算速度。

那么，应该如何选择适当的碰撞体来包裹物体呢？这并没有固定的标准，而是取决于物体本身的形状、用途以及性能需求。例如：

立方体（AABB 或 OBB） 适用于墙壁、箱子等规则物体，计算高效。
球体（Sphere） 适用于圆形物体，如弹珠、行星，旋转无须复杂计算。
胶囊体（Capsule） 常用于人物角色，因为它能更平滑地处理地形变化。
凸包（Convex Hull） 适用于需要更精确碰撞的物体，但计算量比基本几何体高。
网格（Mesh） 只在特殊情况下使用，如静态场景，因其计算复杂度较高。

总之，游戏中的物体通常不会使用完全精确的形状进行碰撞检测，而是根据具体需求选择合适的近似几何体，以在性能与精度之间取得平衡。掌握这些概念，有助于更好地理解后续碰撞检测相关的算法和优化策略。

当然，上述列出的几种情况的碰撞，并不会都在本文中体现，至少目前不会，因此无须担心看完脑壳大的问题。

碰撞检测

有了上述的理解基础，现在可以开始碰撞检测的相关内容了。当我们需要判断确认两个物体(多物体同理)之间是否会发生碰撞时，通常不会使用物体本身的数据作为判断计算的依据，这一点在铺垫内容中已说过，这样做的代价是很高的，真实物体复杂的形状会导致高密度的计算，加剧性能消耗。与此同时，这样的做法也会使得碰撞检测变得异常复杂。

所以，在碰撞检测中，通常使用的是相对简单的几何形状来替代，前面提到过，这样的做法可以大大减少计算量，降低计算的复杂度。究其原因，包括但不限于这些几何形状通常具有很好的数学定义，使得代码也更加容易编写。

虽然简单的几何形状可以方便我们更好的简化计算，总结更加高效的碰撞算法，但是他也存在一定的不足，如果你完全理解了这之前的铺垫内容病结合我们提供的配图，想必对于这样做的不足之处已心里有点B数了吧！

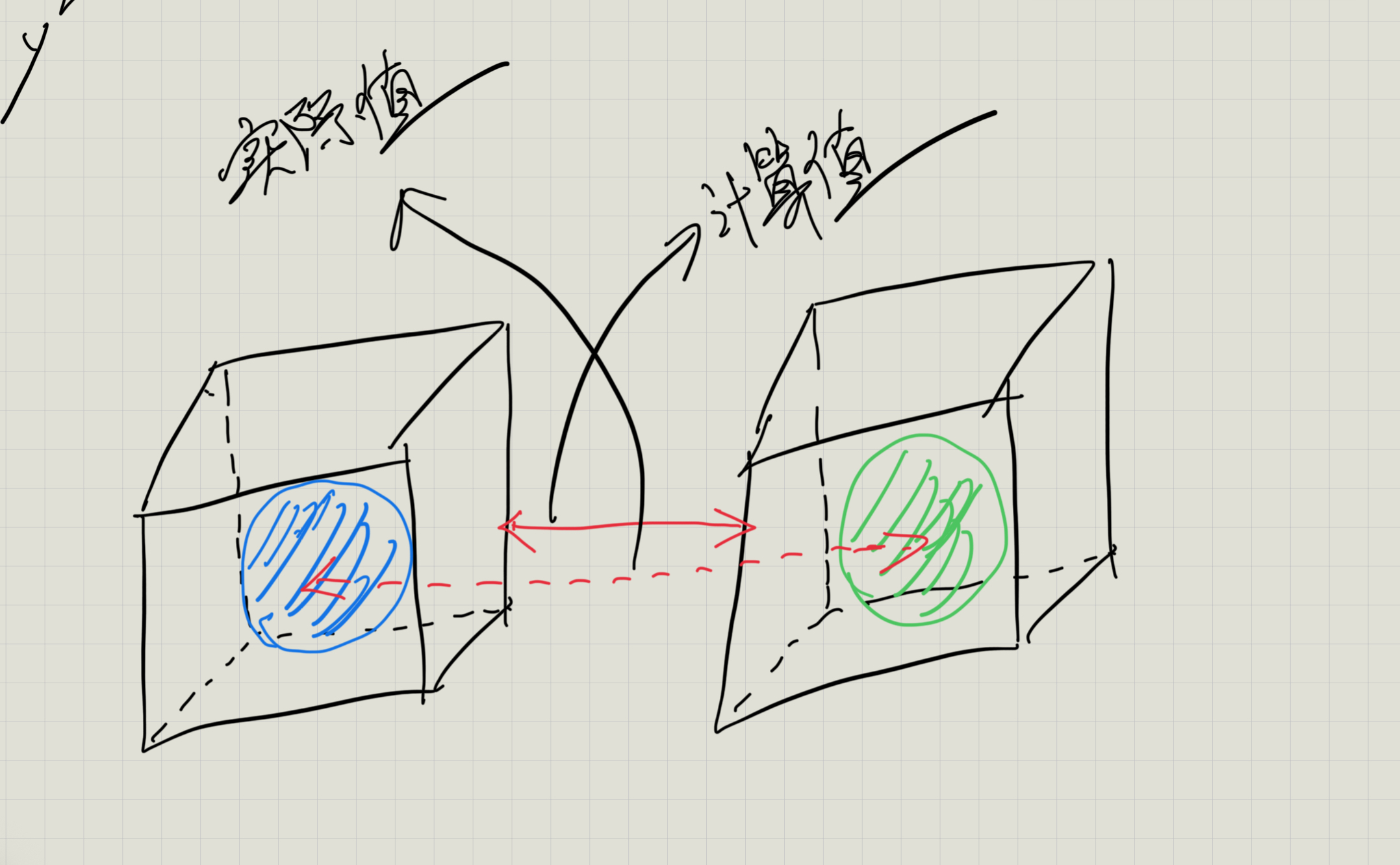
希望就是你想的那样，这样做的一个最突出的不知在于他们不能很好的包裹原物体，比如下面这张途中就是采用了矩形来包裹里面屎黄色甜甜圈。

首先直观的一点是，对于物体本体甜甜圈来说，它仅仅占用来矩形的一部分空间，这导致存在大量的空间冗余，换个角度说就是，这个矩形并没有很好很紧实的将我们的甜甜圈围起来，但是我们在做碰撞检测时，参与计算的实际上就是这个外层的矩形，那么在实际情况下，我们检测到的碰撞可能只是一个近似碰撞，而非精确的碰撞。

所以，通过上面的内容，你应该知道一点，我们讨论的碰撞检测，都是基于包裹在外围的矩形来计算的，因此，在大部分情况下，这会是一个近似值。下图是一个简单的示意图,可以配合理解。

截屏 2025-04-02 22.04.49

AABB和AABB

AABB（Axis-Aligned Bounding Box，轴对齐包围盒）是一种与场景坐标轴对齐的矩形或立方体碰撞形状。它可以用来包围游戏中的物体，并用于高效的碰撞检测。AABB 的概念不仅适用于三维（3D）世界，在二维（2D）环境中也同样适用，区别在于：

3D AABB：边界框沿 x、y、z 轴对齐，通常用来包围立方体或其他三维物体。
2D AABB：边界框仅沿 x、y 轴对齐，适用于二维游戏中的碰撞检测。

AABB 的“轴对齐”意味着它的边缘始终与坐标轴平行，即：

在二维空间，左右边界平行于 y 轴，上下边界平行于 x 轴。
在三维空间，所有六个面都分别与 x、y、z 轴平行，没有旋转。

由于这种固定的对齐方式，AABB 不需要复杂的矩阵运算，而是可以通过简单的数值比较（最小/最大点的重叠判断）来确定两个 AABB 是否发生碰撞。因此，无论是在 2D 还是 3D 环境中，AABB 都是计算两个物体碰撞的最快方法之一，常用于游戏引擎中的初步碰撞检测（Broad Phase）。

判断一个点是否在 AABB 内部非常简单 ,只需要检查该点的坐标是否位于 AABB 的范围内，且需要分别对每个轴进行检查。这是一种常见的判定方法,基于 最小点（Min）和最大点（Max

下面是一个基于2维空间中判断检测的示意图,主要是理解上面的提到的两个最值点的原理:

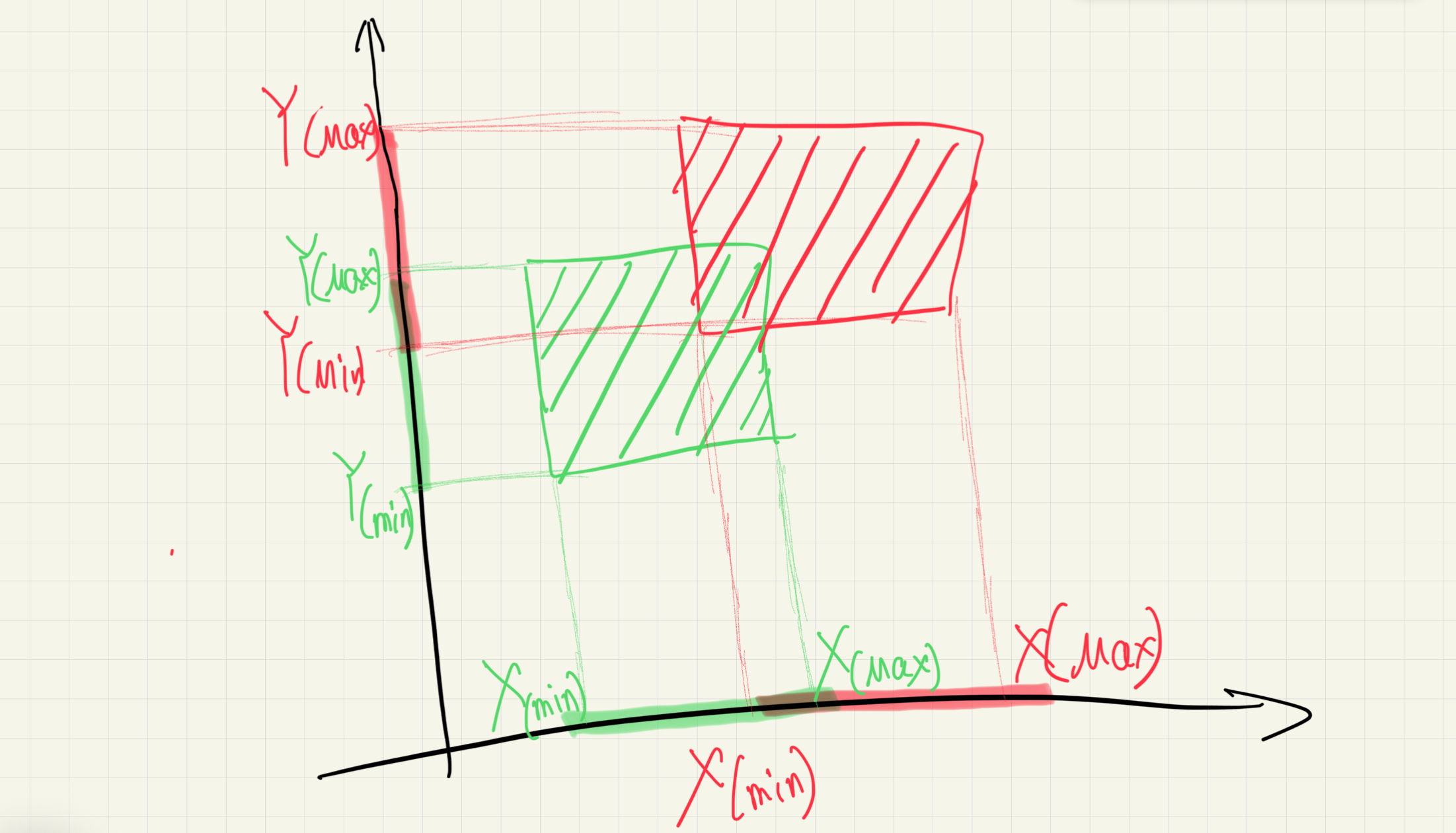
IMG_142305A0761D-1

OK,基于此,我们简化一下该流程,假设我们只在X轴上进行重叠判断,可以得到下面的示意图,对于X,我们只需要判定物体的 $A_(minX)-A(maxX)$ 和 $B_(minX)-B_(maxX)$ 时候重叠。

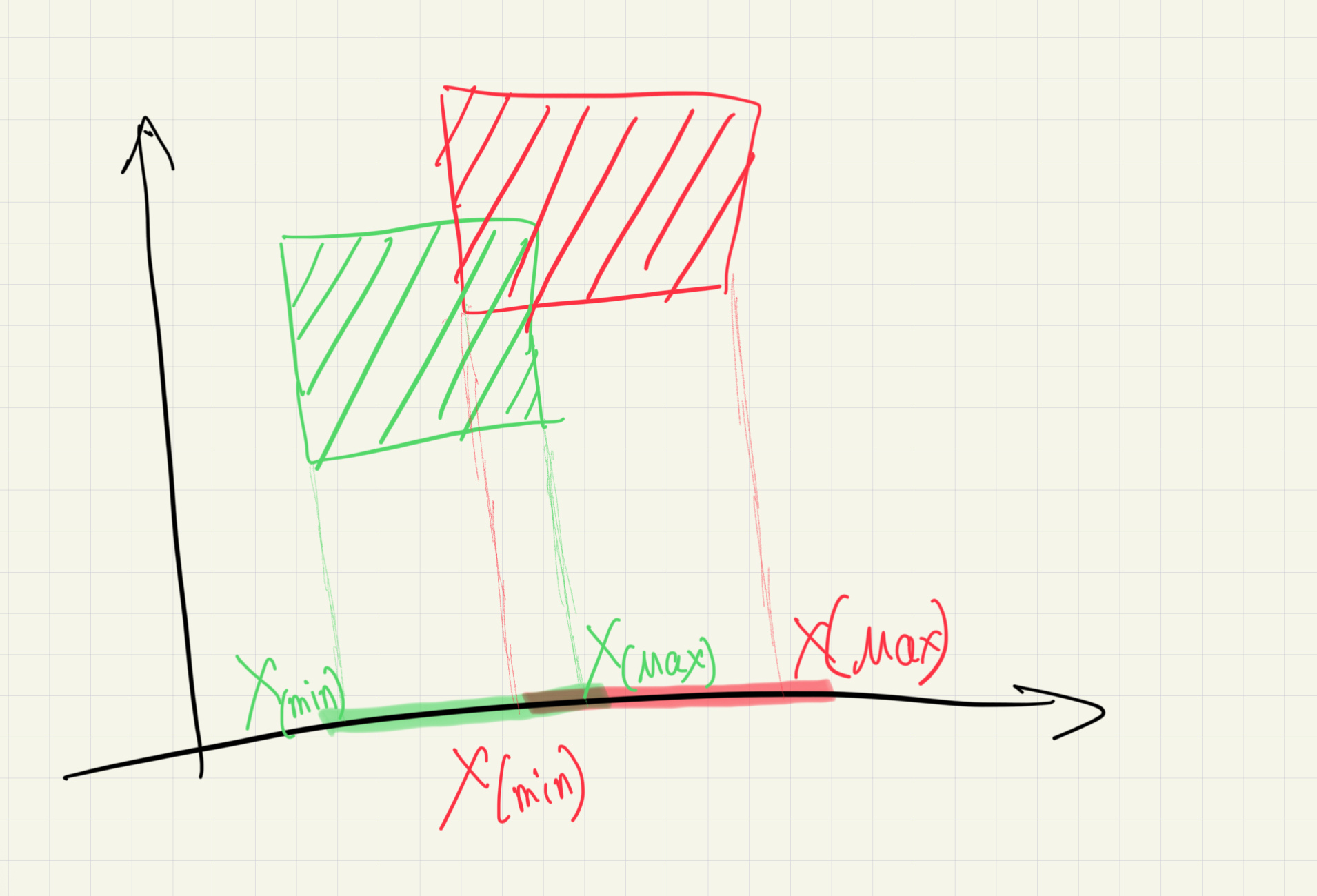
IMG_AEBED0883639-1

原理相似,我们可以很快推导出基于三维空间的重叠判断原理:

如果两个 AABB 在所有轴向上都有重叠，则它们发生碰撞。例如，在 3D 空间中存在两个AABB:

A 的范围为 (A_minX, A_maxX, A_minY, A_maxY, A_minZ, A_maxZ)

B 的范围为 (B_minX, B_maxX, B_minY, B_maxY, B_minZ, B_maxZ)

那么它们发生碰撞的条件可以表示为:

$A_{\text{maxX}} \geq B_{\text{minX}} \quad \text{且} \quad A_{\text{minX}} \leq B_{\text{maxX}}$

$A_{\text{maxY}} \geq B_{\text{minY}} \quad \text{且} \quad A_{\text{minY}} \leq B_{\text{maxY}}$

$A_{\text{maxZ}} \geq B_{\text{minZ}} \quad \text{且} \quad A_{\text{minZ}} \leq B_{\text{maxZ}}$

转化成语言表达就是

X 轴上，A 和 B 有重叠
Y 轴上，A 和 B 有重叠
Z 轴上，A 和 B 有重叠

只有三个轴上都有重叠，两个 AABB 才会发生碰撞。

示例代码:

struct AABB {
   
    Vector3 min;  // AABB 的最小点
    Vector3 max;  // AABB 的最大点

    bool Intersects(const AABB& other) const {
   
        return (max.x >= other.min.x && min.x <= other.max.x) &&
               (max.y >= other.min.y && min.y <= other.max.y) &&
               (max.z >= other.min.z && min.z <= other.max.z);
    }
};