这篇文章包括以下内容哦:
- 汉诺塔问题的定义和背景。
- 解决这个问题所需的思维和逻辑。
- 如何用代码来实现这个思维和逻辑呢?(≧∇≦)/
在学习编程的过程中,汉诺塔问题确实是一个让人头疼的难题呢!函数递归对新手来说确实有点难以理解,但是它又是编程中必不可少的一部分。
我会向大家详细介绍汉诺塔问题以及解题思路,希望能帮助大家更好地理解函数递归的相关知识哦!
汉诺塔的历史背景
汉诺塔问题,也被称为河内塔问题,是一个超级有趣的数学谜题!它起源于古老的印度。听说,在印度的一座寺庙里,有一座神奇的塔。这座塔上有三根针,开始时,有 646464 个不同大小的金盘子,从大到小排列在一根针上。你知道吗?僧侣们每天都要搬动这些金盘子,但是有规定哦!他们只能将一个盘子移动到其他两根针中的一根上,而且绝对不能把大盘子放在小盘子上面。神奇的是,据说当所有的盘子都从初始针移到目标针上时,世界就会迎来末日!
在19世纪,法国的数学家爱德华·卢卡斯研究了这个问题,并找到了解决方法,这让汉诺塔问题变成了著名的计算机科学问题之一。通常,我们可以用递归的方式解决汉诺塔问题,这种方法也是许多编程语言中经典的案例之一。真是太酷了!

这样说可能还是太抽象了,我们可以以两个盘子的汉诺塔为例来进一步说明:
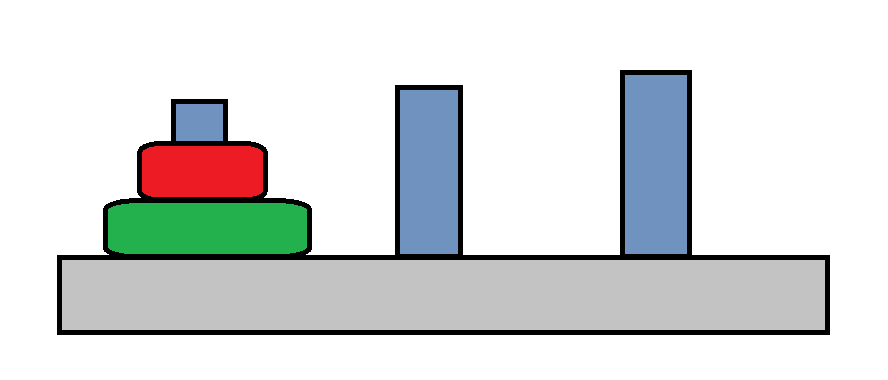
嘻嘻,汉诺塔的核心规则可真是有趣呢!记住两个要点哦:
- 必须把大盘子放在小盘子上面,不能搞错顺序哦!
- 每次只能移动一个盘子,别贪心哦!
我们给每个柱子取了超级可爱的编号,就是从左到右的顺序喔: A 、 B 、 C !使用 X →\rightarrow→ Y 来表示把某个柱子的顶部盘子移到另一个柱子上,其中 X 代表起始柱子, Y 代表目标柱子。举个例子,可以是 A →\rightarrow→ B !现在我们以两个盘子为例子,一起来看看如何移动它们吧!
-
A →\rightarrow→ B
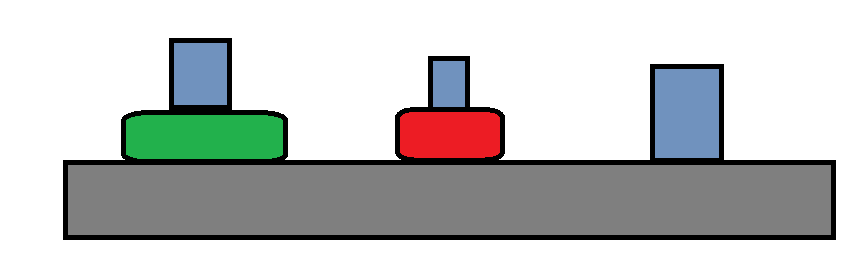
-
A →\rightarrow→ C
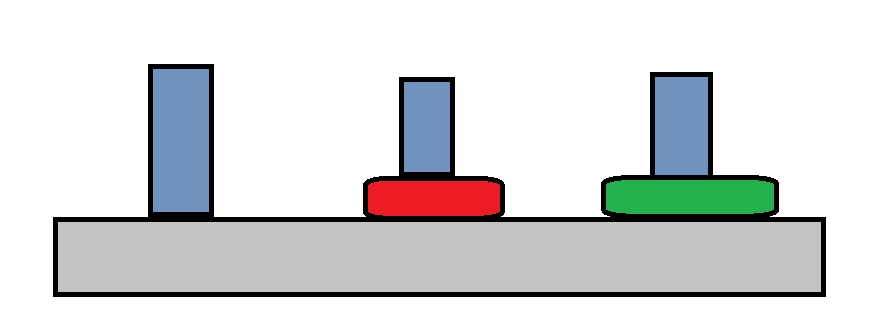
-
B →\rightarrow→ C
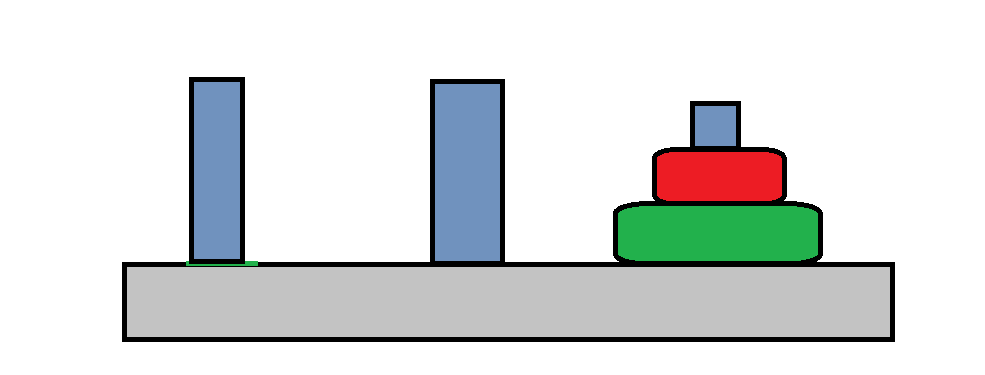
呀,通过简单的逻辑分析,我们已经搞定了两个盘子的汉诺塔问题啦!而且还了解了一些有关历史背景呢!接下来,让我们从特殊情况推广到一般情况,来一起解决 N 个圆盘的汉诺塔问题吧!超级有趣呢!
汉诺塔的思路解析
我们来看看三个汉诺塔问题是怎么解决的吧!
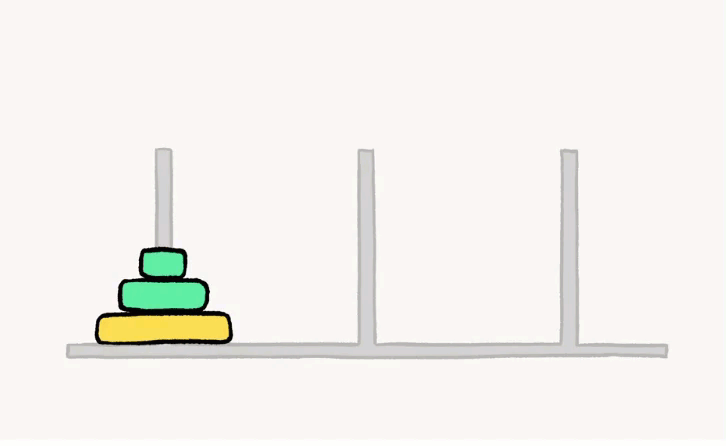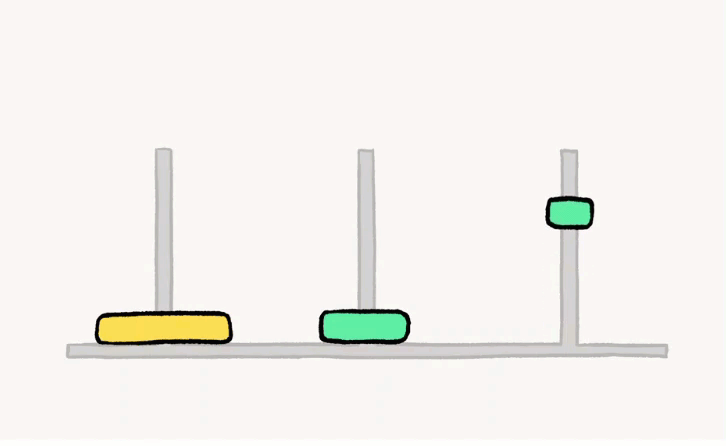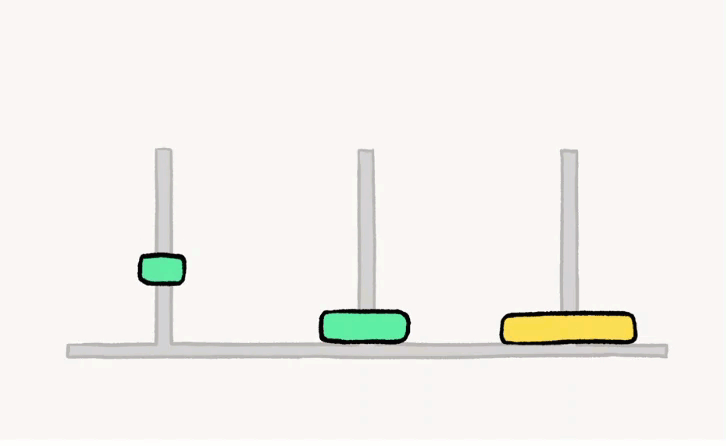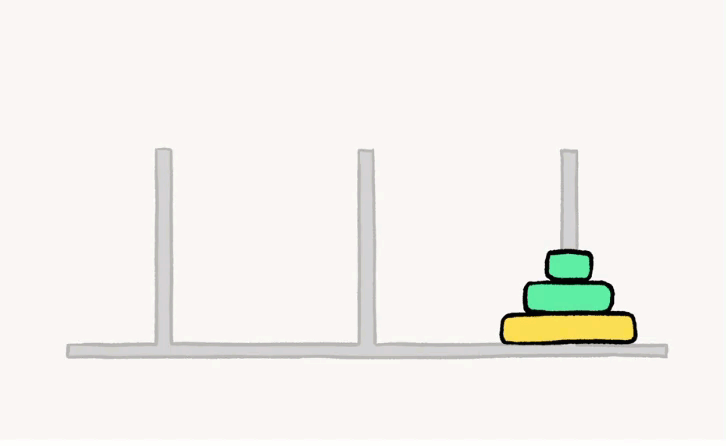
嘻嘻,把步骤拆分后,我们可以得到这七个步骤喔:
- A → C
- A → B
- C → B
- A → C
- B → A
- B → C
- A → C
看起来好复杂啊,我都有点害怕……如果是 444 个、555 个甚至更多的盘子,那可真是难倒人呢!不过别担心,我们有个超级厉害的概念:参考系!
从上面的动图可以看出,如果我们把 A 柱最底下的那个盘子当成地面(就当它不存在啦!),那么我们实际上是在做一个由 A 柱向 B 柱移动两个盘子的汉诺塔问题(之前是由 A 柱移动向 C 柱),然后再把之前在 A 柱当成地面的那个最底层的盘子移动到 C 柱上。接着再做一个由 B 柱向 C 柱移动两个盘子的汉诺塔问题。喏,问题迎刃而解啦!
这种思考方式可以将 NNN 个汉诺塔问题拆分为两个 N−1N-1N−1 的汉诺塔问题再加上一个最底层的参考系移动步骤。我们将解决 NNN 个汉诺塔问题所需步骤数的函数定义为 f(n)f(n)f(n),那么就有:
f(n)={
2f(n−1)+1,n>11,n=1 f(n)=\begin{cases}2f(n-1)+1,&n>1\\1,&n=1\end{cases} f(n)={
2





 本文介绍了汉诺塔问题的定义、历史背景,重点讲解了解决问题的递归思路,通过实例演示和代码实现,帮助读者理解函数递归在编程中的应用。
本文介绍了汉诺塔问题的定义、历史背景,重点讲解了解决问题的递归思路,通过实例演示和代码实现,帮助读者理解函数递归在编程中的应用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 4255
4255

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








