关于《螺旋矩阵》的基础解析

最新推荐文章于 2025-03-15 13:09:39 发布

无须logic ᭄

最新推荐文章于 2025-03-15 13:09:39 发布

阅读量1.5k

点赞数 16

分类专栏： c语言基础文章标签：矩阵算法线性代数 c语言

本文链接：https://blog.csdn.net/2302_79401326/article/details/136101782

版权

c语言基础专栏收录该内容

15 篇文章

订阅专栏

螺旋矩阵的特点就是顺时针从外而内的递增。那么，如何写出螺旋矩阵呢？

螺旋矩阵的写法就是根据它的特点填充元素：

·填充上行从左到右。

·填充右列从上到下。

·填充下行从右到左。

·填充左列从下到上。

同时，我们要注意，如果只是单纯的依据该特点画出正方形的矩阵，我们会发现正方形四个角的位置对应的元素很容易出现重复操作的情况。“不以规矩，不能成方圆”，既然正方形是规则的有规律图形，那么我们也要采用有规律的方法。

我们将每次的填充都采用左闭右开的区间形式，在矩阵边界的末尾留下做下一次的操作。

填充形式示例如下：

1	2	3
8	9	4
7	6	5

不同的颜色代表不同次数的操作，各操作顺时针依次进行。

下面依据题目详细介绍螺旋矩阵的写法以及其中需要注意的判断条件。

例1：给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

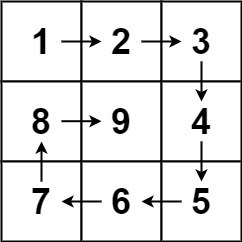
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

思路：承接上述思路，本题从外而内逐层模拟，采用左闭右开的区间，以中间值作为转换内外层的判断条件，n*n即为正方形的大小。注意：当n是奇数时，正方形中心值不能通过操作赋予，需要单独赋值。

int** generateMatrix(int n, int* returnSize, int** returnColumnSizes) {
    *returnSize=n;  
    *returnColumnSizes=(int*)malloc(sizeof(int)*n); //返回的数组大小为n行n列
    int**ans=(int**)malloc(sizeof(int*)*n);
    int i;
    for(i=0;i<n;i++){
        ans[i]=(int*)malloc(sizeof(int)*n);
        (*returnColumnSizes)[i]=n;
    }   //初始化返回的结果数组ans
    int startx=0;
    int starty=0;//循环层数的起始位置
    int mid=n/2;  //定义中间值，最后当n是奇数时在中心填入数字
    int loop=n/2; //层数
    int offset=1;  //偏移数
    int count=1;  //当前需要填充的元素
    while(loop){
        int i=startx;
        int j=starty;
        for(;j<starty+n-offset;j++){
            ans[startx][j]=count++;
        } //模拟上行从左到右
        for(;i<startx+n-offset;i++){
            ans[i][j]=count++;
        } //模拟右列从上到下
        for(;j>starty;j--){
            ans[i][j]=count++;
        }  //模拟下行从右到左
        for(;i>startx;i--){
            ans[i][j]=count++;
        }  //模拟左列从下到上
        offset+=2;  //偏移量每次加2；
        startx++;
        starty++;//起始位置每次加1；
        loop--;
    }
    if(n%2){
            ans[mid][mid]=count; //当n是奇数时单独赋值
        }
        return ans;
}

例2：给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

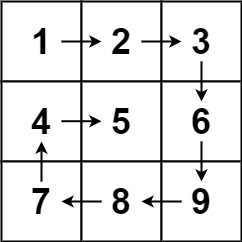
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

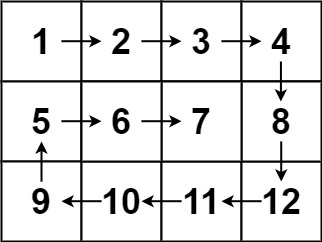
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

思路：在了解螺旋矩阵的写法与原理后，本题的思路就是将螺旋矩阵的写法反其道而行之，将其中的元素列出来。

int* spiralOrder(int** matrix, int matrixSize, int* matrixColSize, int* returnSize) {
    if(matrixSize==0||matrixColSize[0]==0){
        *returnSize=0;
        return NULL;
    }  //判空条件，返回矩阵不存在的情况
    int m=matrixSize,n=matrixColSize[0];
    int*ret=(int*)malloc(sizeof(int)*(m*n));
    *returnSize=0;  
    int left=0,right=n-1,top=0,bottom=m-1;
    while(left<=right&&top<=bottom){
        for(int x=left;x<=right;x++){
            ret[(*returnSize)++]=matrix[top][x];
        }  //上行从左到右
        for(int y=top+1;y<=bottom;y++){
            ret[(*returnSize)++]=matrix[y][right];
        }  //右列从上到下
        if(left<right&&top<bottom){
        for(int x=right-1;x>=left;x--){
            ret[(*returnSize)++]=matrix[bottom][x];
        }  //下行从右到左
        for(int y=bottom-1;y>top;y--){
            ret[(*returnSize)++]=matrix[y][left];
        }  //左列从下到上
         }
         left++;
        right--;
        top++;
        bottom--;
    }
    return ret;
}

例3：给定一个二维数组 array，请返回「螺旋遍历」该数组的结果。

螺旋遍历：从左上角开始，按照向右、向下、向左、向上的顺序依次提取元素，然后再进入内部一层重复相同的步骤，直到提取完所有元素。

示例 1：

输入：array = [[1,2,3],[8,9,4],[7,6,5]]
输出：[1,2,3,4,5,6,7,8,9]

示例 2：

输入：array  = [[1,2,3,4],[12,13,14,5],[11,16,15,6],[10,9,8,7]]
输出：[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]

思路：本题与上题相同，解题代码的区别在于定义了一个新变量代替了（*returnSize）。

int* spiralArray(int** array, int arraySize, int* arrayColSize, int* returnSize) {
    if(arraySize==0||arrayColSize[0]==0){
        *returnSize=0;
        return NULL;
    }
    int m=arraySize,n=arrayColSize[0];
    *returnSize=m*n;
    int*ret=malloc(sizeof(int)*(*returnSize));
    int flag=0;  //定义的新变量作为新数组的元素
    int left=0,right=n-1,top=0,bottom=m-1;
    while(left<=right&&top<=bottom){
        for(int x=left;x<=right;x++){
            ret[flag++]=array[top][x];
        }
        for(int y=top+1;y<=bottom;y++){
            ret[flag++]=array[y][right];
        }
        if(left<right&&top<bottom){
        for(int x=right-1;x>=left;x--){
            ret[flag++]=array[bottom][x];
        }
        for(int y=bottom-1;y>top;y--){
            ret[flag++]=array[y][left];
        }
     }
         left++;
        right--;
        top++;
        bottom--;
    }
    return ret;
}

上述即为对“螺旋矩阵”的基础解析，万事万物皆有规律可循，螺旋矩阵的规律除了从外而内的递增，还有对称，正是对称使得第二题的代码不必将矩阵中心的元素单列出来。代码将数学的规律演绎的栩栩如生，数学使代码的逻辑变得有迹可循，二者浑然一体，才能创造出抽象且具体的螺旋矩阵。

上述题目均来自力扣 (LeetCode) 全球极客挚爱的技术成长平台

借鉴来源代码随想录 (programmercarl.com)