锲而不舍,金石可镂。
打卡第三篇。
A.日期统计

#include<bits.stdc++.h>
using namespace std;
int main() {
int array[100] = {
5, 6, 8, 6, 9, 1, 6, 1, 2, 4, 9, 1, 9, 8, 2, 3, 6, 4, 7, 7,
5, 9, 5, 0, 3, 8, 7, 5, 8, 1, 5, 8, 6, 1, 8, 3, 0, 3, 7, 9,
2, 7, 0, 5, 8, 8, 5, 7, 0, 9, 9, 1, 9, 4, 4, 6, 8, 6, 3, 3,
8, 5, 1, 6, 3, 4, 6, 7, 0, 7, 8, 2, 7, 6, 8, 9, 5, 6, 5, 6,
1, 4, 0, 1, 0, 0, 9, 4, 8, 0, 9, 1, 2, 8, 5, 0, 2, 5, 3, 3
};
int daysInMonth[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int ans = 0;
for (int month = 1; month <= 12; ++month) {
for (int day = 1; day <= daysInMonth[month]; ++day) {
int dateSeq[8] = {2, 0, 2, 3, month / 10, month % 10, day / 10, day % 10};
int k = 0;
for (int i = 0; i < 100; ++i) {
if (array[i] == dateSeq[k]) {
++k;
if (k == 8) {
ans++;
break;
}
}
}
}
}
cout<<ans<<'\n';
return 0;
}B.串的熵

H(S) = -(0的个数 * 0的占比 * log2(0的占比)) - (1的个数 * 1的占比 * log2(1的占))
答案:11027421 。
#include <bits/stdc++.h>
using namespace std;
typedeef long long ll;
const double db = 1e-4;
const ll val = 23333333;
const double sh = 11625907.5798;
int main()
{
ios::sync_with_stdio(0);cin.tie(0); cout.tie(0);
for (ll i = 0; i < val / 2; i++)
{
ll k = val - i;
double sum = -1.0 * i * i / val * log2(1.0 * i / val) - 1.0 * k * k / val * log2(1.0 * k / val);
if (abs(sh - sum) <= db)
{
cout << i << endl;
break;
}
}
return 0;
}
C.冶炼金属



D.飞机降落
正确代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct fly{
ll st,ed,time;
};
ll n;
bool dfs(ll cur_time,ll cnt,vector<ll> &vis,vector<fly> &air){
if(cnt==n){
return true;
}
for(ll i=1;i<=n;i++){
if(vis[i]==0){
if(cur_time<=(air[i].st+air[i].ed)){
vis[i]=1;
ll start_time=max(cur_time,air[i].st);
if(dfs(start_time+air[i].time,cnt+1,vis,air)) return true;
vis[i]=0;
}else continue;
}
}
return false;
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
ll t;cin>>t;
while(t--){
cin>>n;
vector<fly> air(12,{0,0,0});
vector<ll> vis(12,0);
for(ll i=1;i<=n;i++){
cin>>air[i].st>>air[i].ed>>air[i].time;
}
if(dfs(0,0,vis,air))cout<<"YES"<<'\n';
else cout<<"NO"<<'\n';
//air.clear();vis.clear();
}
return 0;
}关于内存分配错误(错误代码)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct fly{
ll st,ed,time;
};
ll n;
vector<fly> air(12,{0,0,0});
vector<ll> vis(12,0);
bool dfs(ll cur_time,ll cnt,vector<ll> &vis,vector<fly> &air){
if(cnt==n){
return true;
}
for(ll i=1;i<=n;i++){
if(vis[i]==0){
if(cur_time<=(air[i].st+air[i].ed)){
vis[i]=1;
ll start_time=max(cur_time,air[i].st);
if(dfs(start_time+air[i].time,cnt+1,vis,air)) return true;
vis[i]=0;
}else continue;
}
}
return false;
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
ll t;cin>>t;
while(t--){
cin>>n;
for(ll i=1;i<=n;i++){
cin>>air[i].st>>air[i].ed>>air[i].time;
}
if(dfs(0,0,vis,air))cout<<"YES"<<'\n';
else cout<<"NO"<<'\n';
air.clear();vis.clear();
}
return 0;
}




所以容器大小和容量还是有区别的,谨慎使用clear();
E.数字接龙

暴力码

#include <bits/stdc++.h>
using namespace std;
// 获取数字的首位数字
int get_first_digit(int num) {
while (num >= 10) {
num /= 10;
}
return num;
}
// 获取数字的末位数字
int get_last_digit(int num) {
return num % 10;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int N;
cin >> N;
vector<int> arr(N);
for (int i = 0; i < N; ++i) {
cin >> arr[i];
}
// dp[i] 表示以第 i 个数结尾的最长接龙子序列的长度
vector<int> dp(N, 1);
// 计算最长接龙数列
for (int i = 1; i < N; ++i) {
for (int j = 0; j < i; ++j) {
// 如果 arr[j] 的末位和 arr[i] 的首位相等
if (get_last_digit(arr[j]) == get_first_digit(arr[i])) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
// 最长接龙数列的长度
int max_chain_len = *max_element(dp.begin(), dp.end());
// 最少删除的元素数量 = 总长度 - 最长接龙数列的长度
cout << N - max_chain_len << endl;
return 0;
}
答案代码:


#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
int n, x, a, p[10] = {0}; // p[10] 是记录尾位为0到9的接龙数列长度
scanf("%d", &n); // 读取序列的长度
for(int i = 0; i < n; i++){
scanf("%d", &a); // 读取每个数字
x = a % 10; // 获取当前数字的末位数字
while(a / 10) a /= 10; // 提取当前数字的首位数字
if(p[a] + 1 > p[x]) p[x] = p[a] + 1; // 更新以 x 为尾的接龙数列长度
}
// 将尾位为 0 到 9 的最大接龙数列长度传给 p[0]
for(int i = 1; i < 10; i++) if(p[i] > p[0]) p[0] = p[i];
// 最少删除的数字数目 = 总数 n - 最长接龙数列的长度
printf("%d", n - p[0]);
return 0;
}
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
ll n;cin>>n;
vector<ll> dp(10,0);
for(ll i=0;i<n;i++){
string x;cin>>x;
dp[x.back()-'0']=max(dp[x.back()-'0'],dp[x.front()-'0']+1);
//比较的并非当前字符串,而是接龙子序列的头部和尾部
//dp[x[x.length()-1]-'0']=max(dp[x[x.length()-1]-'0'],dp[x[0]]+1);
}
sort(dp.rbegin(),dp.rend());
cout<<(n-dp[0]);
return 0;
}
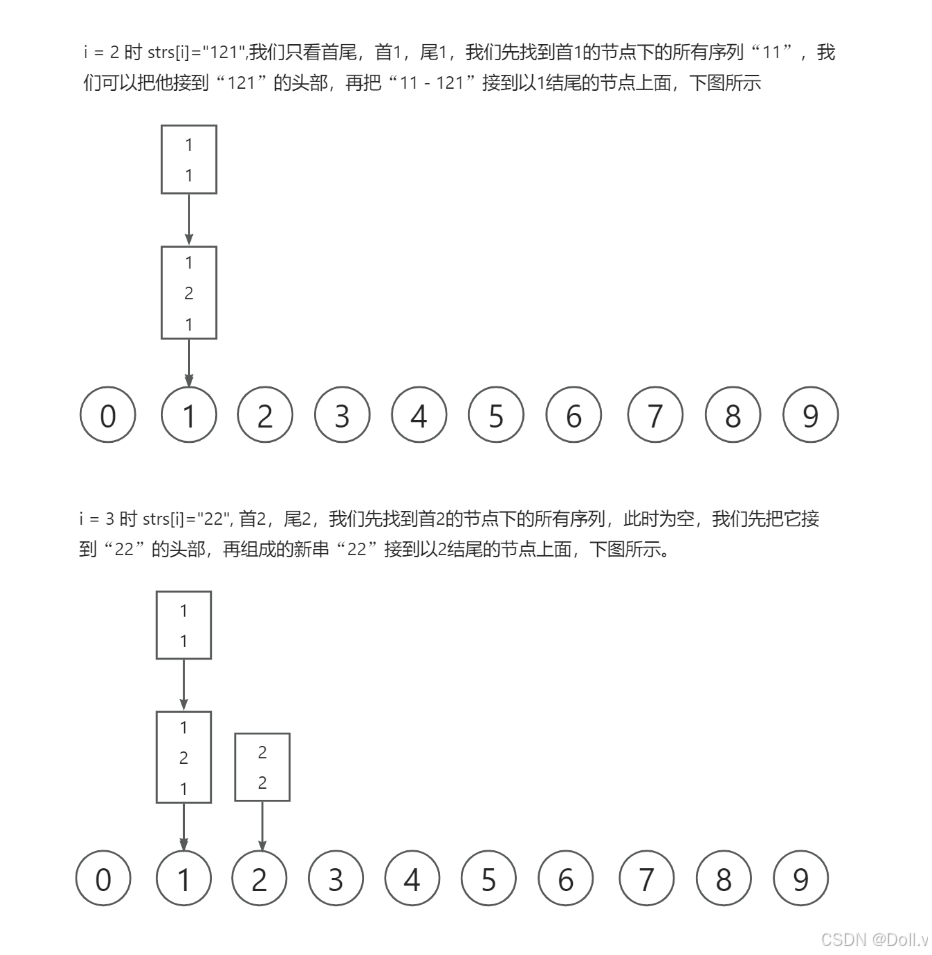


F.岛屿个数


方法:
2次bfs
#include <stdio.h> //引入库函数 输入输出
#include <string.h>// 字符串与memset
#include <stdbool.h>//bool类型
#include <stdlib.h>//malloc
char grid[55][55]; //记录数组
bool visit[55][55]; //访问状态数组
int seax[8]={0,0,-1,1,1,1,-1,-1}; //海水方向盘
int seay[8]={1,-1,0,0,-1,1,1,-1};
int roadx[4]={0,0,-1,1}; //陆地方向盘
int roady[4]={1,-1,0,0};
bool check(int i,int j,int m,int n){ //check方法
if(i<0 || j<0 || i>=m || j>=n){
return false;
}
return true;
}
void bfs_road(int x,int y,int m,int n){ //bfs遍历陆地方法 与遍历海洋思路相同,不赘述
int quene[2555][2];
int first=0;
int rear=0;
visit[x][y]=true;
quene[rear][0]=x;
quene[rear][1]=y;
rear++;
while(first<rear){
int i=quene[first][0];
int j=quene[first][1];
first++;
for(int k=0;k<4;++k){
int ni=i+roadx[k];
int nj=j+roady[k];
if(check(ni,nj,m,n) && grid[ni][nj]=='1' && visit[ni][nj]==false){
visit[ni][nj]=true;
quene[rear][0]=ni;
quene[rear][1]=nj;
rear++;
}
}
}
}
int bfs_sea(int x,int y,int m,int n,int ans){ //bfs遍历海洋方法
int quene[2555][2]; //C语言用数组模拟队列,根据变量范围确定数量大小
int first=0; //队列首
int rear=0;//队列尾
visit[x][y]=true;//将该点设为已访问过
quene[rear][0]=x;//将该点加入队列
quene[rear][1]=y;
rear++;//队列尾自增
while(first<rear){ //当队列中还有元素
int i=quene[first][0];//抽出目前的元素
int j=quene[first][1];
first++;//队列首自增
for(int k=0;k<8;++k){//调用方向盘找旁边的元素
int ni=i+seax[k];
int nj=j+seay[k];
if(check(ni,nj,m,n) && grid[ni][nj]=='0' && visit[ni][nj]==false ){//满足两大条件 且还是海
visit[ni][nj]=true; //将该点设为已访问,加入队列继续寻找旁边的岛屿
quene[rear][0]=ni;
quene[rear][1]=nj;
rear++;
}
if(check(ni,nj,m,n) && grid[ni][nj]=='1' && visit[ni][nj]==false ){//满足两大条件 且是陆地
ans++; //找到岛屿了,数量+1
bfs_road(ni,nj,m,n);//用bfs访问整个岛屿,防止重复计算
}
}
}
return ans; //返回最终得出的岛屿数量
}
int main(){ //主方法
int T;
scanf("%d",&T); //读入T
int *ans = (int*)malloc(sizeof(int)*T); //创造一个长度为T的数组,每个元素记录该组数据有几个岛屿
for(int k=0;k<T;++k){ //对T组数据进行一一判定
int m,n;
scanf("%d %d",&m,&n); //读入行列
for(int i=0;i<m;++i){ //读入地图
scanf("%s",&grid[i]);// 这里要注意输入的是字符串,看好类型
}
bool flag=false; //如果整个地图外围就是一个大环,全都是陆地,flag一直是false,会返回岛屿数目为1
memset(visit,false,sizeof(visit)); //设定全图为未访问状态
int anss=0; //定义岛屿数目变量为0
for(int i=0;i<m;++i){ //双重for循环遍历整个地图
for(int j=0;j<n;++j){
if(i==0 || i==m-1 || j==0 || j==n-1){ //先从外面边界遍历 防止遍历里面遍历到环的内部
if(visit[i][j]==false && grid[i][j]=='0' ){//如果找到了边界的海
flag=true; //地图不是一个大环
anss=bfs_sea(i,j,m,n,anss);//调用dfs方法返回岛屿数目
}
}
}
}
if(flag==false){ //如果整个地图外围就是一个大环,会返回岛屿数目为1
anss=1;
}
ans[k]=anss;//记录该组数据岛屿数目
}
for(int i=0;i<T;++i){ //分行输出存储的岛屿数目数组
printf("%d\n",ans[i]);
}
return 0; //返回值
}
bfs+dfs
#include<bits/stdc++.h>
using namespace std;
const int N = 50+10;
string a[N];//地图
bool v[N][N];//标记是否访问
int s,w,ans=0;//s,w地图大小
int lx[]={1,0,-1,0};//4个方向向量
int ly[]={0,-1,0,1};//lx,ly为岛屿探索4个方向
int hx[]={1,0,-1,0,1,1,-1,-1} ;//hx,hy为海的8个方向
int hy[]={0,-1,0,1,-1,1,1,-1};
bool check(int x,int y);//检查数组下标是否合理
void bfs (int x,int y);
void dfs(int x,int y) ;
void bfs(int x,int y){
if(!check(x,y)) return;//下标不合理
v[x][y]=true; //标记访问
for(int i=0;i<8;i++){//8个方向依次探索
if(check(x+hx[i],y+hy[i])&&!v[x+hx[i]][y+hy[i]]){//可以访问的下一块区域
if(a[x+hx[i]][y+hy[i]]=='1') {//下一块区域 是岛屿
dfs(x+hx[i],y+hy[i]);//先标记所有与他相连的岛屿
ans++;//岛屿数量加1
}
else {
bfs(x+hx[i],y+hy[i]);//下一块区域 是海,深入探索
}
}
}
}
void dfs(int x,int y){
if(!check(x,y)) return ;//下标不合理
v[x][y] = true; //标记访问
for(int i=0;i<4;i++){//4个方向依次探索
//可以访问该方向的岛屿
if(check(x+lx[i],y+ly[i])&&a[x+lx[i]][y+ly[i]]=='1'&&!v[x+lx[i]][y+ly[i]]){
dfs(x+lx[i],y+ly[i]);//继续寻找相连岛屿
}
}
}
bool check(int x,int y){
return (x>=0&&x<s&&y>=0&&y<w);
}
void solve(){//读取数据
memset(v,false,sizeof(v));//初始或重置标记数组
cin>>s>>w;
for(int i=0;i<s;i++){
cin>>a[i];
}
//寻找4边的海域作为着点,注意循环条件不要重复顶点
for(int i=0;i<w;i++){
if(a[0][i]=='0') {
bfs(0,i);
}
if(a[s-1][i]=='0'){
bfs(s-1,i);
}
}
for(int i=1;i<s-1;i++){
if(a[i][0]=='0') {
bfs(i,0);
}
if(a[i][w-1]=='0'){
bfs(i,w-1);
}
}
cout<<ans<<endl;
ans = 0;
}
int main()
{
int t=1;
cin>>t;
while(t--){
solve();
}
return 0;
}2次dfs(染色+合并)(Floodfill算法(泛洪填充算法))




#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
// 四连通方向,用于 DFS2(陆地内部的搜索)
ll dx[] = {-1, 1, 0, 0};
ll dy[] = {0, 0, -1, 1};
// 八连通方向,用于 DFS1(水域外部的搜索)
ll sx[] = {-1, 1, 0, 0, -1, -1, 1, 1};
ll sy[] = {0, 0, -1, 1, -1, 1, -1, 1};
ll m, n; // 注意:这里 m 表示行数,n 表示列数
/*
dfs1:从外部水域出发,以八连通方式搜索,将所有与外部连通的水域标记为 '2'。
参数说明:
st, ed —— 当前搜索点的行和列下标
mp —— 地图,传递时必须按引用传递,才能修改原数组
vis —— 访问标记数组,标记某个格子是否已访问过
*/
void dfs1(ll st, ll ed, vector<vector<char>> &mp, vector<vector<ll>> &vis) {
mp[st][ed] = '2'; // 将当前水域标记为 '2'
vis[st][ed] = 1; // 同时标记为已访问
for (ll i = 0; i < 8; i++) {
ll nx = st + sx[i];
ll ny = ed + sy[i];
// 地图大小为 (m+2) x (n+2)(包含外围的海水)
if (nx >= 0 && nx <= m + 1 && ny >= 0 && ny <= n + 1 &&
!vis[nx][ny] && mp[nx][ny] == '0') {
dfs1(nx, ny, mp, vis);
}
}
}
/*
dfs2:从陆地出发,以四连通方式搜索,将整个岛屿区域标记为 '2',避免重复计数。
参数说明:
st, ed —— 当前搜索点的行和列下标
mp —— 地图,按引用传递,修改原数组
vis —— 访问标记数组
*/
void dfs2(ll st, ll ed, vector<vector<char>> &mp, vector<vector<ll>> &vis) {
mp[st][ed] = '2'; // 标记当前陆地为 '2'
vis[st][ed] = 1; // 标记为已访问
for (ll i = 0; i < 4; i++) {
ll nx = st + dx[i];
ll ny = ed + dy[i];
// 陆地区域只在原地图内部,即行在 [1, m],列在 [1, n]
if (nx >= 1 && nx <= m && ny >= 1 && ny <= n &&
!vis[nx][ny] && mp[nx][ny] == '1') {
dfs2(nx, ny, mp, vis);
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
ll t;
cin >> t;
while (t--) {
// 输入地图行数 m 和列数 n(原题中 m,n 代表地图尺寸)
cin >> m >> n;
// 构造一个比原地图大一圈的二维数组,行数 = m+2,列数 = n+2,初始全部填充为 '0'(海水)
vector<vector<char>> mp(m + 2, vector<char>(n + 2, '0'));
// 构造与 mp 同尺寸的访问标记数组,初始全为 0(表示未访问)
vector<vector<ll>> vis(m + 2, vector<ll>(n + 2, 0));
// 读入实际地图数据存放在 mp 的内部区域(1 ≤ i ≤ m, 1 ≤ j ≤ n)
for (ll i = 1; i <= m; i++) {
for (ll j = 1; j <= n; j++) {
cin >> mp[i][j];
}
}
// 第一次 DFS:从外部的 (0,0) 点出发,以八连通方式将所有与外界连通的海水标记为 '2'
dfs1(0, 0, mp, vis);
// 合并岛屿内部的水域:将未被 dfs1 标记的 '0'(即岛屿内部的水)变为 '1'
for (ll i = 1; i <= m; i++) {
for (ll j = 1; j <= n; j++) {
if (mp[i][j] == '0')
mp[i][j] = '1';
}
}
// 在进行 DFS2 之前,重置访问标记数组 vis 为 0,
// 因为之前 DFS1 的访问标记不能用于 DFS2
for (ll i = 0; i < m + 2; i++) {
for (ll j = 0; j < n + 2; j++) {
vis[i][j] = 0;
}
}
ll cnt = 0; // 用于计数岛屿数量
// 第二次 DFS:遍历内部区域(1 ≤ i ≤ m, 1 ≤ j ≤ n),
// 对每个未被标记的陆地('1')启动 DFS2,并计数一个岛屿
for (ll i = 1; i <= m; i++) {
for (ll j = 1; j <= n; j++) {
if (mp[i][j] == '1') {
cnt++;
dfs2(i, j, mp, vis);
}
}
}
cout << cnt << '\n';
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
const int N = 60;
int g[N][N];
int t, n, m, cnt;
int dx1[] = {0, 0, 1, -1}, dy1[] = {1, -1, 0, 0};
int dx2[] = {-1, -1, -1, 0, 1, 1, 1, 0}, dy2[] = {-1, 0, 1, 1, 1, 0, -1, -1};
bool st[N][N];
void dfs_1(int x, int y)
{
st[x][y] = true; // 标记当前陆地已访问
for (int i = 0; i < 4; i++)
{
int tx = dx1[i] + x, ty = dy1[i] + y;
// 判断 (tx,ty) 是否在地图内部(注意陆地只存在于 [1, n]×[1, m])、
// 并且没有被访问过,同时该点是陆地(g[tx][ty] 非 0)
if (tx >= 1 && tx <= n && ty >= 1 && ty <= m && !st[tx][ty] && g[tx][ty])
dfs_1(tx, ty);
}
}
void dfs_2(int x, int y)
{
st[x][y] = true; // 标记当前点已访问(这里主要是水域)
for (int i = 0; i < 8; i++)
{
int tx = x + dx2[i], ty = y + dy2[i];
// 判断 (tx,ty) 是否在扩展后的地图内:行范围为 [0, n+1],列范围为 [0, m+1]
if (tx >= 0 && tx <= n + 1 && ty >= 0 && ty <= m + 1 && !st[tx][ty])
// 如果 (tx,ty) 是海水(即 g[tx][ty] == 0),则继续用 DFS_2 遍历水域
if (!g[tx][ty]) dfs_2(tx, ty);
else // 如果 (tx,ty) 是陆地(g[tx][ty]==1)
{
dfs_1(tx, ty); // 用 DFS_1 遍历整块陆地(岛屿)
cnt++; // 每发现一块岛屿就计数一次
}
}
}
int main()
{
scanf("%d", &t);
while (t--)
{
cnt = 0;
memset(g, 0, sizeof g); // 将整个 g 数组初始化为 0(海水)
memset(st, false, sizeof st); // 将访问标记全部置为 false
scanf("%d%d", &n, &m);
// 读入实际地图数据到 g[1..n][1..m],注意外围边界保持为 0(海水)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
char x;
cin >> x;
g[i][j] = x - '0'; // 将字符 '0' 或 '1' 转为整型 0 或 1
}
// 从 (0,0) 开始,进行 DFS_2,遍历所有与外部水域连通的区域,
// 同时在遍历过程中遇到陆地就用 DFS_1 将整个岛屿淹没,并计数
dfs_2(0, 0);
// 输出计数结果:即外部水域与之相连的岛屿数量
printf("%d\n", cnt);
}
return 0;
}
#include using namespace std;
int m, n;
vector d;
bool v[51][51];
bool flag;
int d1[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
int d2[8][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}, {1, 1}, {1, -1}, {-1, -1}, {-1, 1}};
/**
* 将问题看做从一个岛屿(x, y)点向外扩散红色水
* 大陆上是4通路扩散,到海里就是8通路扩散
* 为啥大陆上要4通路,因为如下两座岛,是不相连的,但是在大陆上8通路就会认为相连:
* 100
* 010
* 000
* 如果当前红色水扩散到地图边界了(要出地图了),就表示当前(x, y)出来的岛屿不是子岛屿,答案就加一
* 扩散的时候,标记岛屿不再访问了,但是海水访问过的要复原,以便下次访问
*/
void flooding(int x, int y, int bak) {
// printf("%d %d %d\n", x, y, bak);
// 如果扩散到边界了,说明当前岛屿没有被其他岛屿包住,不是子岛屿
if (x < 0 || x >= m || y < 0 || y >= n) {flag = true; return;}
int nb = d[x][y] == '0' ? 0 : 1; // 当前地块的种类,存整数
if (bak == 0 && nb == 1) return; // 如果从0到1,就表示从海水碰到其他岛屿边界了,停止扩散了
if (v[x][y]) return; // 如果已经访问过了,那么就不继续扩散了
v[x][y] = true;
if (nb == 1) { // 如果当前是岛屿,这时已经默认从1扩散到1的,就继续向4通路扩散
for (auto [a, b] : d1) flooding(x + a, y + b, nb);
}
if (nb == 0) { // 如果当前是海水,这时不论是从0/1扩散到0的,就继续向8通路扩散
for (auto [a, b] : d2) flooding(x + a, y + b, nb);
}
}
// 复原海水的访问状态
void flush_zero() {
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (v[i][j] && d[i][j] == '0') v[i][j] = false;
}
}
}
int main() {
int T;
cin >> T;
while (T--) {
cin >> m >> n;
d.clear();
memset(v, false, sizeof(v));
for (int i = 0; i < m; i++) {
string s;
cin >> s;
d.push_back(s);
}
int ans = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (d[i][j] == '0' || v[i][j]) continue;
flag = false;
flooding(i, j, 1);
if (flag) ans++;
flush_zero();
}
}
cout << ans << endl;
}
return 0;
}
G.子串简写

暴力代码

#include <iostream>
#include <string>
using namespace std;
int main() {
int K;
cin >> K;
string S;
char c1, c2;
cin >> S >> c1 >> c2;
if(S=="abababdb"&&c1=='a'&&c2=='b'){
cout<<6;
return 0;
}
int count = 0;
int n = S.length();
// 枚举所有子串的起始位置 i
for (int i = 0; i < n; ++i) {
// 枚举所有子串的结束位置 j
for (int j = i + K - 1; j < n; ++j) { // 子串的长度必须大于等于 K
if (S[i] == c1 && S[j] == c2) {
++count;
}
}
}
cout << count << endl;
return 0;
}
正确答案:
1.直接暴力遍历出c1,c2的位置数组,以及c1,c2的数量。
2.遍历c1,c2数组,用双循环,每一个c1第一次匹配成功c2后边的c2是一定可以匹配这个c1的,时记录该c2的位置,并且下一个c1直接从该位置开始匹配c2.

我服了,有个细节点很重要。。。c1可以等于c2,题目没说不可以。



#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
ll k;cin>>k;
string s;char c1,c2;cin>>s>>c1>>c2;
vector<ll> x,y;
for(ll i=0;i<s.length();i++){
if(s[i]==c1)x.push_back(i);
else if(s[i]==c2)y.push_back(i);
}
//for(ll i=0;i<x.size();i++)cout<<x[i]<<" ";
//cout<<endl;
//for(ll i=0;i<y.size();i++)cout<<y[i]<<" ";
ll count=0;
ll i=0,j=0;
while(i<x.size()&&j<y.size()){
if(y[j]-x[i]+1>=k){
count+=(y.size()-j);
//效率更高并且防止重复计数
i++;
}else j++;
}
cout<<count;
return 0;
}
/*
0 2 4
1 3 5 7
会有重复的被计数
*/H.整数删除 

数组模拟双向链表
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
ll v[N], l[N], r[N];
//双向链表的删除操作, 删除x结点
void del(int x) {
r[l[x]] = r[x], l[r[x]] = l[x];
v[l[x]] += v[x], v[r[x]] += v[x];
}
int main () {
int n, k; cin >> n >> k;
//最小堆, 堆中的元素是{权值, 结点下标}
priority_queue<pair<ll, int>, vector<pair<ll, int>>, greater<pair<ll, int>>> h;
//输入并构造双向链表
r[0] = 1, l[n + 1] = n;
for (int i = 1; i <= n; i ++)
cin >> v[i], l[i] = i - 1, r[i] = i + 1, h.push({v[i], i});
while (k --) {
auto p = h.top(); h.pop();
//如果v发生变化, 则目前的元素不一定是最小值, 需要重新放入堆中
if (p.first != v[p.second]) h.push({v[p.second], p.second}), k ++;
else del(p.second);
}
//输出链表剩余的元素
int head = r[0];
while (head != n + 1) {
cout << v[head]<< " ";
head = r[head];
}
return 0;
}#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll,ll> PII;
const ll N=5e5+10;
ll l[N],r[N],e[N];
void remove(ll x){///x是坐标标号
e[l[x]]+=e[x];
e[r[x]]+=e[x];
l[r[x]]=l[x];
r[l[x]]=r[x];
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
ll n,k;cin>>n>>k;
r[0]=1;
l[n+1]=n;
priority_queue<PII,vector<PII>,greater<PII>> pq;//先存值,再存坐标
for(ll i=1;i<=n;i++){
cin>>e[i];
l[i]=i-1,r[i]=i+1;
pq.push({e[i],i});
}
while(k--){
ll x=pq.top().first;
ll y=pq.top().second;
pq.pop();
if(x==e[y])remove(y);
else{
pq.push({e[y],y});
k++;
continue;
}
}
for(ll i=r[0];i<=n;i=r[i]){///注意好怎么输出的
cout<<e[i]<<" ";
}
return 0;
}
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
typedef long long ll;
typedef pair<ll,int> P;
const int N = 5e5+10;
//l[i]代表i下标的左边下标,r[i]代表i下标的右边下标,v[i]是i下标的值 例如:
//数据1 2 3 4 5,(1序) 其中v[1] = 1;v[5]=5;l[2]=1(第二个数据的左边是第一个);r[3]=4;(第3个数据的右边是第4个)
ll l[N],r[N],v[N];
int n;
int k;
//删除操作
void del(int id){
//假设数据为1 2 3 4 5
//把id右边个体的左编号改为id的左编号
//假设id=2;就让3的左编号(l[3])从原来的2改为1
l[r[id]] = l[id];
//把id左边个体的右编号改为id的右编号
//假设id=2;就让1的右编号(r[1])从原来的2改为3
r[l[id]] = r[id];
// 至此最小数就相当于被删除(跟左右编号数组没有了联系)
//以下 为相邻数据加上最小值
v[r[id]]+=v[id];
v[l[id]]+=v[id];
}
int main(){
cin>>n>>k;
//初始化0的右编号为1,n+1的左编号为n
r[0] = 1;
l[n+1] = n;
//创建优先队列,将数据排序,top()弹出的值就是最小值
priority_queue<P,vector<P>,greater<P> > pr;
//依次输入数据
for(int i=1;i<=n;i++){
int a;
cin>>a;
v[i]=a;
l[i]=i-1;//i左编号为i-1
r[i]=i+1;//i右编号为i+1
pr.push({a,i});//将{值,编号}压入最小队列
}
while(k--){
auto [vl,id] = pr.top();//得到最小值vl和对应的编号id
pr.pop();//删除最小值
//我们删除时对相邻数据的增加只是针对于v[]数组,最小队列中的值没有改变
//所以要判断弹出来的最小值是否跟最初值一致
if(vl!=v[id]){//弹出来的最小值是否跟最初值不同,说明删除其他数据时该数据得到了增加
pr.push({v[id],id});//重新压入值(更新后的值)和编号进行排序
k++;//这一次没有进行删除最小值操作,故k自增一次
continue;
}
else del(id);//弹出来的最小值是否跟最初值一致,就执行删除操作
}
for(int i=r[0];i<=n;i=r[i]){//输出剩余的数
cout<<v[i]<<" ";
}
return 0;
}stl 模板库双向链表
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
ll v[N], l[N], r[N];
//双向链表的删除操作, 删除x结点
void del(int x) {
r[l[x]] = r[x], l[r[x]] = l[x];
v[l[x]] += v[x], v[r[x]] += v[x];
}
int main () {
int n, k; cin >> n >> k;
//最小堆, 堆中的元素是{权值, 结点下标}
priority_queue<pair<ll, int>, vector<pair<ll, int>>, greater<pair<ll, int>>> h;
//输入并构造双向链表
r[0] = 1, l[n + 1] = n;
for (int i = 1; i <= n; i ++)
cin >> v[i], l[i] = i - 1, r[i] = i + 1, h.push({v[i], i});
while (k --) {
auto p = h.top(); h.pop();
//如果v发生变化, 则目前的元素不一定是最小值, 需要重新放入堆中
if (p.first != v[p.second]) h.push({v[p.second], p.second}), k ++;
else del(p.second);
}
//输出链表剩余的元素
int head = r[0];
while (head != n + 1) {
cout << v[head]<< " ";
head = r[head];
}
return 0;
}I.景区导游 (日后补题)

对于 100% 的数据,2 ≤ K ≤ N ≤ 1e5,1 ≤ u, v, Ai ≤ N,1 ≤ t ≤ 1e5。保证Ai 两两不同。
(tarjan算法求LCA),解题思路:利用公式dis[a]-dis[b]-2*dis[lca(a,b)]求出a与b之间的距离,dis为此节点到根节点的距离,解题思路:
游览顺序为2 6 5 1,当跳过中间某个景点时(例如6)要花费的时间为总时间减去该景点与前一个景点的时间(2->6),再减去该景点与后一个景点的时间(6->5),最后再加上前一个景点的时间到后一个景点的时间(2->5),跳过第一个或者最后一个时只需要减去后一段或前一段时间;
接下来是引入最小公共祖先(用的是数链剖分)优化后的代码
#include#define ll long long
using namespace std;
typedef pair pii;
const int N = 1e5+10;
map id;
vectoredge[N];
int n,m;
ll sum[N];//sum[i]表示i这个点到我们指定的根节点u的时间 要开long long
//树链剖分:
int fa[N],son[N],sz[N];//fa[u]存u的父节点,son[u]u的重儿子,sz[u]u为根节点的子树节点数(包括自己)
int top[N],dep[N];//top[u]指u所在的重链顶点(是一个轻儿子节点) dep[u]u所在的层级
//以上部分数组再后面都要初始化为0
void dfs1(int u,int father){//完善 fa[],sz[],dep[]
fa[u] = father,dep[u] = dep[father] + 1,sz[u] = 1;//sz[u] = 1自己
for(int v : edge[u]){
if(v==father) continue;
dfs1(v,u);
sz[u] += sz[v];//节点大小加上子节点的大小
if(sz[son[u]] < sz[v]) son[u] = v;
}
}
//初始调用dfs2(1,1)
void dfs2(int u,int t){//完善top[]
top[u] = t;
if(!son[u]) return ;//没有重儿子就返回
dfs2(son[u],t);//如果有重儿子就深入遍历 连接这一条重儿子链top都为t
for(int v : edge[u]) {
if(v==fa[u] || v==son[u]) continue;//重儿子和父节点不在遍历
dfs2(v,v);//轻儿子节点的top为他自己
}
}
int lca(int u,int v){//找两个节点的最小公共祖先
while(top[u]!=top[v]){//u,v节点不在一条重链上
if(dep[top[u]] < dep[top[v]]) swap(u,v);//让u始终为重链顶点更深的那一方
u = fa[top[u]] ;//u向上跳
}
return dep[u] < dep[v] ? u : v;//返回u,v层次更低的那一方
}
//树链剖分--end
void cal_sum(int u){//初始化sum数组
for(int v : edge[u]){
if(v==fa[u]) continue;//防止1到2又从2到1
//假设支链1->3->5,5到1的时间为3到5的时间加上3到1的时间
sum[v] = id[{v,u}] + sum[u];
cal_sum(v);
}
}
void solve(){
//数据初始化
memset(sz,0,sizeof(sz));
memset(dep,0,sizeof(dep));
memset(son,0,sizeof(son));
memset(sum,0,sizeof(sum));
cin>>n>>m;
int s[m];
for(int i=1;i>x>>y>>l;
edge[x].push_back(y);
edge[y].push_back(x);
id[{x,y}] = id[{y,x}] = l;
}
for(int i=0;i>s[i];
}
dfs1(1,0);
dfs2(1,1);
cal_sum(1);//指定1为根节点sum数组记录了每个点到1的时间
//数据初始化 end
ll sum_ = 0;//原始浏览景点的总时间
for(int i=0;i<m-1;i++){
//此时任意两个点u,v之间的时间为: u到1的时间加上v到1的时间
//减去2倍的多余部分时间(多余部分是指最小公共祖先到1的时间) 注意乘上2
sum_ += sum[s[i]] + sum[s[i+1]] - 2*sum[lca(s[i],s[i+1])];
}
//以下部分思路与暴力一致
for(int i=0;i<m;i++){
ll temp = sum_;
if(i==0){
temp -= sum[s[i]] + sum[s[i+1]] - 2*sum[lca(s[i],s[i+1])];
}
else if(i==m-1){
temp -= sum[s[i-1]] + sum[s[i]] - 2*sum[lca(s[i-1],s[i])];
}
else{
temp -= sum[s[i-1]] + sum[s[i]] - 2*sum[lca(s[i-1],s[i])];
temp -= sum[s[i]] + sum[s[i+1]] - 2*sum[lca(s[i],s[i+1])];
temp += sum[s[i-1]] + sum[s[i+1]] - 2*sum[lca(s[i-1],s[i+1])];
}
cout<<temp<<" ";
}
}
int main(){
solve();
return 0;
}J. 砍树(日后补题)
对于每一对 (ai,bi),ai 到bi之间的边都可以砍掉;
把可以砍掉的边权值+1,那么这条边的权值w表示砍掉这条边可以满足w对(ai,bi)不连通;
最后找到权值等于m且编号最大的删去即可,若没找到则代表无解;
树上差分,LCA算法。
例样的树
1 22 34 32 56 5


#includeusing namespace std;
typedef pair pii;
const int N = 1e5+10;
map id;
vectore[N];//存图
int n,m;
//树链剖分:
int fa[N],son[N],sz[N];//fa[u]存u的父节点,son[u]u的重儿子,sz[u]u为根节点的子树节点数(包括自己)
int top[N],dep[N];//top[u]指u所在的重链顶点(是一个轻儿子节点) dep[u]u所在的层级
//初始化为0
void dfs1(int u,int father){//完善 fa[],sz[],dep[],son[]
fa[u] = father,dep[u] = dep[father] + 1,sz[u] = 1;//sz[u] = 1自己
for(int v : e[u]){
if(v==father) continue;
dfs1(v,u);
sz[u] += sz[v];//节点大小加上子节点的大小
if(sz[son[u]] < sz[v]) son[u] = v;
}
}
//初始调用dfs2(1,1)
void dfs2(int u,int t){//完善top[]
top[u] = t;
if(!son[u]) return ;//没有重儿子就返回
dfs2(son[u],t);//如果有重儿子就深入遍历 连接这一条重儿子链top都为t
for(int v : e[u]) {
if(v==fa[u] || v==son[u]) continue;//重儿子和父节点不在遍历
dfs2(v,v);//轻儿子节点的top为他自己
}
}
int lca(int u,int v){//找两个节点的最小公共祖先
while(top[u]!=top[v]){//u,v节点不在一条重链上
if(dep[top[u]] < dep[top[v]]) swap(u,v);//让u始终为重链顶点更深的那一方
u = fa[top[u]] ;//u向上跳
}
return dep[u] < dep[v] ? u : v;//返回uv层次更低的那一方
}
//可能用到:
int w[N];
void cal_w(int u){//w[i]表示边权 用他下面一个顶点的点权记录
for(int v : e[u]){
if(v==fa[u]) continue;
cal_w(v);
w[u] += w[v];
}
}
void solve(){
//数据初始化
memset(sz,0,sizeof(sz));
memset(dep,0,sizeof(dep));
memset(son,0,sizeof(son));
memset(w,0,sizeof(w));
cin>>n>>m;
for(int i=1;i>x>>y;
e[x].push_back(y);
e[y].push_back(x);
id[{x,y}] = id[{y,x}] = i;
}
dfs1(1,0);
dfs2(1,1);
for(int i=0;i>x>>y;
//用到树差分的边差分:
//对两点路径边的权值加1等价于两点权值加1,最小公共祖先-2
//不详细介绍证明
w[x]++;w[y]++;
w[lca(x,y)]-=2;
}
cal_w(1);//各边的权值
int ans = 0;
for(int i=1;i<=n;i++){
if(w[i]==m){//满足条件的边权
int id_ = id[{i,fa[i]}];//用的点权记录边权,记录的是他和他父节点的之间的边权
ans = max(ans,id_);//边的编号最大
}
}
cout<<ans;
}
int main(){
solve();
return 0;
}end....
























 2597
2597

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








