一.最短路径
1.Floyd-Warshall算法
单源最短路径弗洛伊德(Floyd)算法,用于求解图结构中各顶点之间的最短路径。
有n个地方,m条从x到y的路线,距离为z,这是有向图,有箭头的,只限与x到y。接下来请看模板代码。
输入:
4 8
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12正常路线是这样的
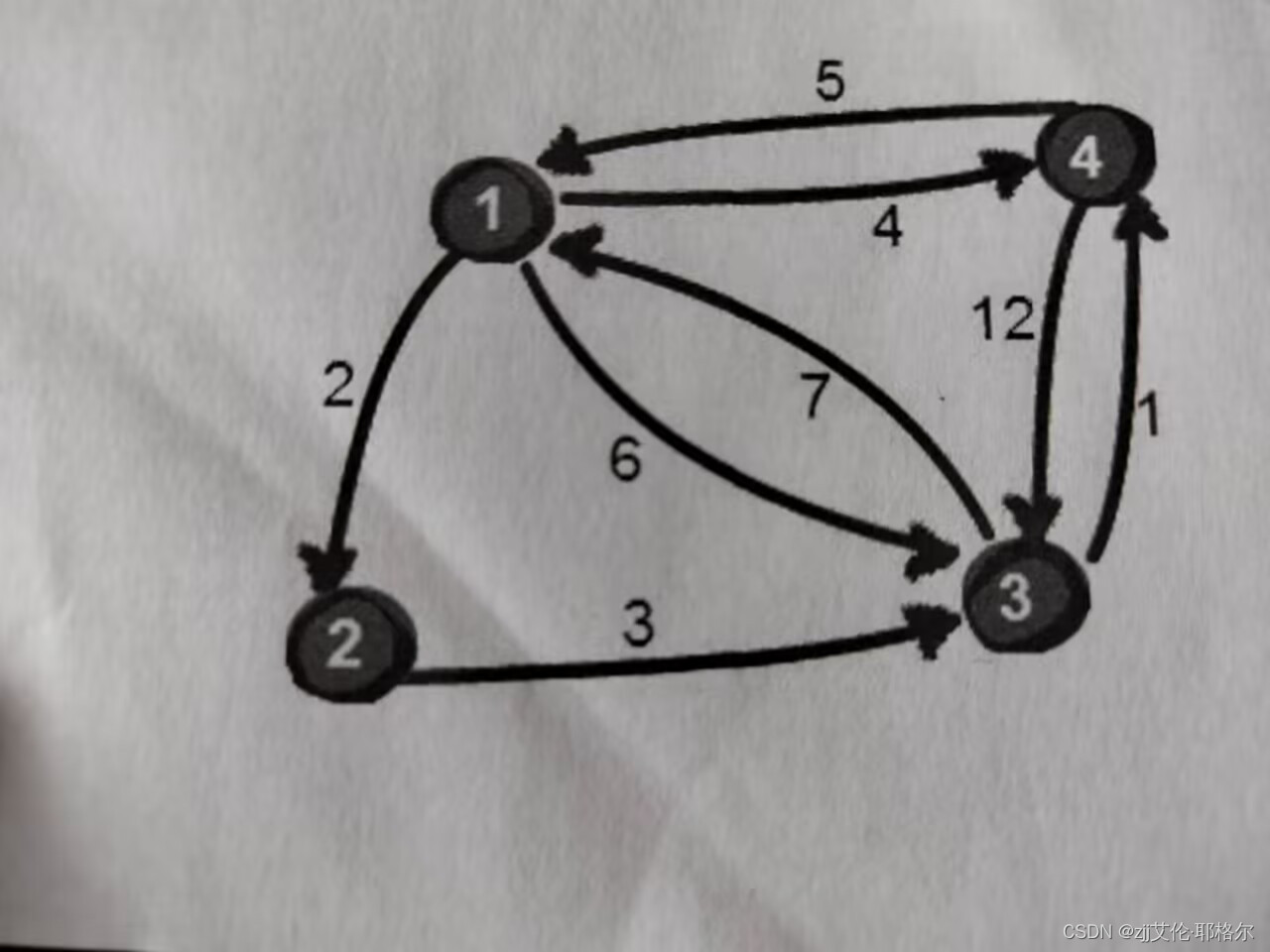
因为有的地方无法直达,所以在这里就把它设置为无穷大。转变后是这样的,外面的数字分别表示i和j,是坐标,1到1,所以是0,输入中有(1 2 2),所以1到2,是2。i表示行着的,j表示竖着的,这样就好理解了吧。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
const long long inf=0x3f3f3f3f;
int a[N][N],b[N];
int n,m;
int main() {
cin>>n>>m; //n个地方,m条路线
for(int i=1; i<=n; i++) {
for(int j=1; j<=n; j++) {
if(i!=j)
a[i][j]=inf; //最大值
}
}
int x,y,z;
for(int i = 1; i <=m; i ++) { //m条路线的距离
cin>>x>>y>>z;
a[x][y]=z;
}
for(int k=1; k<=n; k++) { //这三个循环是Floyd-Warshall算法的核心代码
for(int i=1; i<=n; i++) { //a[i][j]表示i到j的最短距离
for(int j=1; j<=n; j++) { //意思是从i出发,经过k,然后到达j。
if(a[i][k]<inf&&a[k][j]<inf) //防止数值大小超出int
a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
}
}
}
for(int i=1; i<=n; i++) {
for(int j=1; j<=n; i++) {
printf("%5d ",a[i][j]);
}
printf("\n");
}
return 0;
}
2.Dijkstra算法(单源最短路)
只要用于求一个点到其他点的最短距离,但是不能用于解决负权边的图,即权值为负数。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
const long long inf=0x3f3f3f3f;//用inf(infinity的缩写)存储一个我们认为的正无穷值
int e[N][N],book[N],dis[N];
int n,m,i,j,t1,t2,t3,u,v,mi;
int main() {
//读入n和m,n表示顶点个数,m表示边的条数
scanf("%d %d",&n,&m);
//初始化
for(i=1; i<=n; i++)
for(j=1; j<=n; j++)
if(i==j) e[i][j]=0;
else e[i][j]=inf;
//读入边
for(i=1; i<=m; i++) {
scanf("%d %d %d",&t1,&t2,&t3);
e[t1][t2]=t3;
}
//初始化dis数组,这里是1号顶点到其余各个顶点的初始路程
for(i=1; i<=n; i++)
dis[i]=e[1][i];
//book数组初始化
for(i=1; i<=n; i++)
book[i]=0;
book[1]=1;
//Dijkstra算法核心语句
for(i=1; i<=n-1; i++) {
//找到离1号顶点最近的顶点
mi=inf;
for(j=1; j<=n; j++) {
if(book[j]==0 && dis[j]<mi) {
mi=dis[j];
u=j;
}
}
book[u]=1;
for(v=1; v<=n; v++) {
if(e[u][v]<inf) {
if(dis[v]>dis[u]+e[u][v])
dis[v]=dis[u]+e[u][v];
}
}
}
//输出最终的结果
for(i=1; i<=n; i++)
printf("%d ",dis[i]);
getchar();
getchar();
return 0;
}
输入:
6 9
1 2 1
1 3 12
2 3 9
3 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4
输出:
0 1 8 4 12 173.spfa算法
队列优化,去掉一些无用的松弛操作,用队列来维护松弛造作的点。继承了Bellman-Ford算法的思想,但时间复杂度相对来说提高了很多。
与BFS的算法有一些类似,利用了STL队列。
注意:spfa能处理负权边。
注意:虽然大多数情况spfa跑的比较快,但时间复杂度仍为(Onm),主要用应用于有负边权的情况(如果没有负边权,推荐使用Dijkstra算法)。利用了邻接表建图,数据结构的基础一定要掌握好,而且该算法很容易超时,被卡,必须要谨慎选择该算法。
算法分析:
1.用dis数组记录点到有向图的任意一点距离,初始化起点距离为0,其余点均为INF,起点入队。
2.判断该点是否存在。(未存在就入队,标记)
3.队首出队,并将该点标记为没有访问过,方便下次入队。
4.遍历以对首为起点的有向边(t,i),如果dis[i]>dis[t]+w(t,i),则更新dis[i]。
5.如果i不在队列中,则入队标记,一直到循环为空。
实战题目1的代码,在题目的最下面,spfa。
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10; //范围
int k=0; //全局变量
struct sb {
int next,to,dis;//下一个(尾巴),去哪里,距离
} num[N];
int head[N]; //下一个的上一个,就是头
const int inf=2147483647;//最大值
bool vis[N];
int dis[N];
void fun(int a,int b,int c) {
num[++k].next=head[a];
num[k].to=b;
num[k].dis=c;
head[a]=k;
}
int main() {
int n,m,ans;
cin>>n>>m>>ans; //城市,路,城市ans(求城市ans到各个城市的最短距离)
for(int i=1; i<=m; i++) { //m条路
int e,r,t;
cin>>e>>r>>t;
fun(e,r,t);
}
queue<int>q; //队列
for(int i=1; i<=n; i++) {
dis[i]=inf;
vis[i]=0;
}
q.push(ans);
dis[ans]=0;
vis[ans]=1;
while(!q.empty()) {
int u=q.front();
q.pop();
vis[u]=0;
for(int i=head[u]; i; i=num[i].next) { //这里的u是,起点ans,head[u]代表是i前面的一个数,而它后面的数就是num[i].next(下一个),从head[u]直接跳到num[i].next
int v=num[i].to; 遍历以i为起点的边
if(dis[v]>dis[u]+num[i].dis) {
dis[v]=dis[u]+num[i].dis;
if(!vis[v]) {
vis[v]=1;
q.push(v);
}
}
}
}
for(int i=1; i<=n; i++)
printf("%d ",dis[i]);
return 0;
}4.Bellman-Frod———解决负权边
这个也是核心代码只有三行的算法。
for(int k=1; k<=n-1; k++) //Bellman-Rord核心语句
for(int i=1; i<=m; i++)
dis[v[i]]=min(dis[v[i]],dis[u[i]]+w[i]);一样的,n个地方,m条路。
输入:
5 5
2 3 2
1 2 -3
1 5 5
4 5 2
3 4 3输出:
0 -3 -1 2 4#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
const long long inf=0x3f3f3f3f;
int u[N],w[N],v[N],dis[N]; //起点,终点,两者的距离,最短距离
int n,m,t=0,sum=0;
int main() {
cin>>n>>m; //n个地方,m条路线
for(int i=1; i<=m; i++)
cin>>u[i]>>v[i]>>w[i]; //起点,终点,两者距离
for(int i=1; i<=n; i++)
dis[i]=inf; //初始化dis数组,这里是1号到各个顶点的最短距离
dis[1]=0;
for(int k=1; k<=n-1; k++) //Bellman-Rord核心语句
for(int i=1; i<=m; i++)
dis[v[i]]=min(dis[v[i]],dis[u[i]]+w[i]);
for(int i=1; i<=n; i++)
printf("%d ",dis[i]);
return 0;
}
检查是否含有负权回路
for(int k=1; k<=n-1; k++) //Bellman-Rord核心语句
for(int i=1; i<=m; i++)
dis[v[i]]=min(dis[v[i]],dis[u[i]]+w[i]);
int flag=0; //检查负权回路
for(int i=1; i<=m; i++)
if(dis[v[i]]>dis[u[i]]+w[i])
flag=1;
if(flag)printf("此图含有负权回路\n");稍微优化一下下(不更新,提取结束循环)
#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
const long long inf=0x3f3f3f3f;
int u[N],w[N],v[N],dis[N]; //起点,终点,两者的距离,最短距离
int n,m,t=0,sum=0;
int main() {
cin>>n>>m; //n个地方,m条路线
for(int i=1; i<=m; i++)
cin>>u[i]>>v[i]>>w[i]; //起点,终点,两者距离
for(int i=1; i<=n; i++)
dis[i]=inf; //初始化dis数组,这里是1号到各个顶点的最短距离
dis[1]=0;
for(int k=1; k<=n-1; k++) { //Bellman-Rord核心语句
int check=0;
for(int i=1; i<=m; i++) {
if(dis[v[i]]>dis[u[i]]+w[i]) {
dis[v[i]]=dis[u[i]]+w[i];
check=1;
}
}
if(check==0)break; //如果没有更新,提取结束循环,节省时间
}
// int flag=0; //检查负权回路
// for(int i=1; i<=m; i++)
// if(dis[v[i]]>dis[u[i]]+w[i])
// flag=1;
// if(flag)printf("此图含有负权回路\n");
for(int i=1; i<=n; i++)
printf("%d ",dis[i]);
return 0;
}5.Bellman-Ford的队列优化
书中有一个很好的概括,为什么会出现无效松弛?即每一次松弛后都会有顶点已经求得最短路,要是换作在Dijkstra,是要被book数组标记1的。那这些就是后续不用松弛的,而哪些边需要继续松弛?即最短路径信息dis[]发生变化的顶点的所有出边都要松弛。
简单解释一下:如果有一个顶点(非起始点)到起始点的距离变化了——即它的dis[]数组变化了,那么它的所有出边(即以它为起点的边)都要进行松弛,即再次判断这些出边抵达的点,到起始点的距离是否能够缩短。
如何记录哪些是发生变化的点,怎么样找到与发生变化的点的所有出边?这样我们用到队列来优化,并用邻接表进行存储(这样就能线性找到相关的所有出边)
代码如下:
#include <stdio.h>
int main()
{
int i, j, k;
int n, m;
int first[10], next[10]; // first应该比n大1,next应该比m大1
int u[10], v[10], w[10];
int que[10];
int head = 1, tail = 1;
int book[10] = {0};
int dis[10];
int inf = 99999;
printf("请输入图的结点数和边数:\n");
scanf("%d %d", &n, &m);
for (i = 1; i <= n; i++)//dis数组初始化
dis[i] = inf;
dis[1] = 0;
for (i = 1; i <= n; i++)//邻接表初始化
first[i] = -1;
printf("请输入相邻有边的结点和其边权:\n");
for (i = 1; i <= m; i++)
{
scanf("%d %d %d", &u[i], &v[i], &w[i]);
next[i] = first[u[i]];//将边的信息存进邻接表
first[u[i]] = i;
}
que[tail] = 1;//初始化队列
que[tail] = 1;
tail++;
book[1] = 1;
while (head < tail)
{
k = first[que[head]];
while (k != -1) //只分析当前头结点的每一条边
{
if (dis[v[k]] > dis[u[k]] + w[k])
{
dis[v[k]] = dis[u[k]] + w[k];
if (book[v[k]] == 0)//如果能够松弛,且边所抵达的结点还没确定
{
que[tail] = v[k];//让它入队,进队后,就能再判断它的所有出边了
tail++;
book[v[k]] = 1;
}
}
k = next[k];//找相关结点的下一条出边
}
book[head] = 0;//这步很关键,后续还可能松弛。
head++;//分析完所有出边后,头结点出队
}
for (i = 1; i <= n; i++)
printf("%d ", dis[i]);
}
6.四种算法的区别
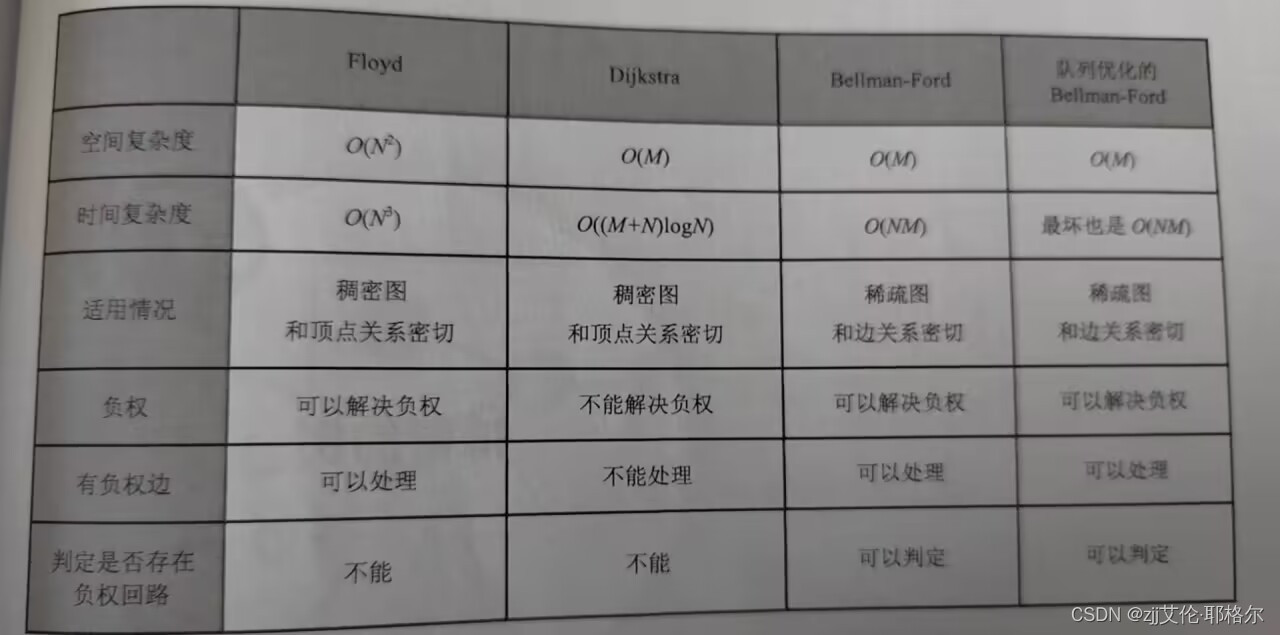
Floyd算法虽然总体时间复杂度高,但是可以处理带有负权边的图(但不能有负权回路) 并且均摊到每一点对上,在所有的算法中还是属于较优的。另外,Floyd算法较小的编码复杂度也是它的一大优势。所以,如果要求的是所有点对间的最短路径,或者如果数据范围较小,则Floyd算法比较适合。Djkstra算法最大的弊端是它无法处理带有负权边以及负权回路的图,但是Dijkstra具有良好的可扩展性,扩展后可以适应很多问题。另外用堆优化的Dijkstra算法的时间复杂度可以达到O(MlogM)。当边有负权,甚至存在负权回路时,需要使用Bellman-Ford算法或者队列优化的Bellman-Ford算法。因此我们选择最短路径算法时,要根据实际需求和每一种算法的特性,选择适合的算法。
二.实战题目
1.题目:【模板】单源最短路径(弱化版)

输入:
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4输入:
0 2 4 3正常的Dijkstra,没优化的,实际上数据过不了,因为二维数组存不下。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
const long long inf=0x3f3f3f3f;//用inf(infinity的缩写)存储一个我们认为的正无穷值
int e[N][N],book[N],dis[N];
int n,m,i,j,t1,t2,t3,u,v,mi;
int main() {
//读入n和m,n表示顶点个数,m表示边的条数
scanf("%d %d",&n,&m);
//初始化
for(i=1; i<=n; i++)
for(j=1; j<=n; j++)
if(i==j) e[i][j]=0;
else e[i][j]=inf;
//读入边
for(i=1; i<=m; i++) {
scanf("%d %d %d",&t1,&t2,&t3);
e[t1][t2]=t3;
}
//初始化dis数组,这里是1号顶点到其余各个顶点的初始路程
for(i=1; i<=n; i++)
dis[i]=e[1][i];
//book数组初始化
for(i=1; i<=n; i++)
book[i]=0;
book[1]=1;
//Dijkstra算法核心语句
for(i=1; i<=n-1; i++) {
//找到离1号顶点最近的顶点
mi=inf;
for(j=1; j<=n; j++) {
if(book[j]==0 && dis[j]<mi) {
mi=dis[j];
u=j;
}
}
book[u]=1;
for(v=1; v<=n; v++) {
if(e[u][v]<inf) {
if(dis[v]>dis[u]+e[u][v])
dis[v]=dis[u]+e[u][v];
}
}
}
//输出最终的结果
for(i=1; i<=n; i++)
printf("%d ",dis[i]);
getchar();
getchar();
return 0;
}
那就看看其他大佬写的优化版本!
**1.**定义ans[100000],ans[i]代表到达i点的最小花费
**2.**定义bool数组visit,代表是否来过这里
- 注意:这里的访问过,是指“以这个点为中心计算过”,而不是ans值被更新过
**2.**ans[起点]=0,其余的赋值为inf
**3.**定义一个curr变量,visit[current]=1(访问过),代表现在的位置,初始值为起点。
**4.**列举所有与curr相联通的的点,将这些点(i)的ans值更新:
ans[i]=min(ans[i],ans[curr]+到这些点需要的花费 )
5. 列举所有没有过的的点,找到ans值最小的点,赋值给curr,visit[current]=1(访问过)
6 所有点都访问过(visit[i]都==1),程序结束。此时,ans[i]代表从起点到i的最短路径
#include<iostream>
using namespace std;
int head[100000],cnt;
long long ans[1000000];
bool vis[1000000];
int m,n,s;
struct edge
{
int to;
int nextt;
int wei;
}edge[1000000];
void addedge(int x,int y,int z)
{
edge[++cnt].to=y;
edge[cnt].wei=z;
edge[cnt].nextt=head[x];
head[x]=cnt;
}
int main()
{
cin>>m>>n>>s;
for(int i=1;i<=n;i++)
{
ans[i]=2147483647;
}
ans[s]=0;
for(int i=1;i<=n;i++)
{
int a,b,c;
cin>>a>>b>>c;
addedge(a,b,c);
}
int pos=s;
while(vis[pos]==0)
{
long long minn=2147483647;
vis[pos]=1;
for(int i=head[pos];i!=0;i=edge[i].nextt)
{
if(!vis[edge[i].to]&&ans[edge[i].to]>ans[pos]+edge[i].wei)
{
ans[edge[i].to]=ans[pos]+edge[i].wei;
}
}
for(int i=1;i<=m;i++)
{
if(ans[i]<minn&&vis[i]==0)
{
minn=ans[i];
pos=i;
}
}
}
for(int i=1;i<=m;i++)
{
cout<<ans[i]<<' ';
}
}还有这个spfa!
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10; //范围
int k=0; //全局变量
struct sb {
int next,to,dis;//下一个(尾巴),去哪里,距离
} num[N];
int head[N]; //下一个的上一个,就是头
const int inf=2147483647;//最大值
bool vis[N];
int dis[N];
void fun(int a,int b,int c) {
num[++k].next=head[a];
num[k].to=b;
num[k].dis=c;
head[a]=k;
}
int main() {
int n,m,ans;
cin>>n>>m>>ans; //城市,路,城市ans(求城市ans到各个城市的最短距离)
for(int i=1; i<=m; i++) { //m条路
int e,r,t;
cin>>e>>r>>t;
fun(e,r,t);
}
queue<int>q; //队列
for(int i=1; i<=n; i++) {
dis[i]=inf;
vis[i]=0;
}
q.push(ans);
dis[ans]=0;
vis[ans]=1;
while(!q.empty()) {
int u=q.front();
q.pop();
vis[u]=0;
for(int i=head[u]; i; i=num[i].next) { //这里的u是,起点ans,head[u]代表是i前面的一个数,而它后面的数就是num[i].next(下一个),从head[u]直接跳到num[i].next
int v=num[i].to; 遍历以i为起点的边
if(dis[v]>dis[u]+num[i].dis) {
dis[v]=dis[u]+num[i].dis;
if(!vis[v]) {
vis[v]=1;
q.push(v);
}
}
}
}
for(int i=1; i<=n; i++)
printf("%d ",dis[i]);
return 0;
}2.题目:【模板】单源最短路径(标准版)

输入:
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4输出:
0 2 4 3
#include<bits/stdc++.h>
#define M(x,y) make_pair(x,y)
using namespace std;
int fr[100010],to[200010],nex[200010],v[200010],tl,d[100010];
bool b[100010];
void add(int x,int y,int w){
to[++tl]=y;
v[tl]=w;
nex[tl]=fr[x];
fr[x]=tl;
}
priority_queue< pair<int,int> > q;
int main(){
int n,m,x,y,z,s;
scanf("%d%d%d",&n,&m,&s);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
}
for(int i=1;i<=n;i++) d[i]=1e10;
d[s]=0;
q.push(M(0,s));
while(!q.empty()){
int x=q.top().second;
q.pop();
if(b[x]) continue;
b[x]=1;
for(int i=fr[x];i;i=nex[i]){
int y=to[i],l=v[i];
if(d[y]>d[x]+l){
d[y]=d[x]+l;
q.push(M(-d[y],y));//懒得重载运算符
}
}
}
for(int i=1;i<=n;i++) printf("%d ",d[i]);
return 0;
}3.题目:医院设置

输入:
5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0Floyd算法!!!
#include<cstdio>
using namespace std;
int a[101],g[101][101];
int main()
{
int n,l,r,min,total;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
g[i][j]=1000000;
}
}
for(int i=1;i<=n;i++)//读入、初始化
{
g[i][i]=0;
scanf("%d%d%d",&a[i],&l,&r);
if(l>0)g[i][l]=g[l][i]=1;
if(r>0)g[i][r]=g[r][i]=1;
}
for(int k=1;k<=n;k++)//用Floyed求任意两结点之间的最短路径
{
for(int i=1;i<=n;i++)
{
if(i!=k)
{
for(int j=1;j<=n;j++)
{
if(i!=j&&k!=j&&g[i][k]+g[k][j]<g[i][j])
g[i][j]=g[i][k]+g[k][j];
}
}
}
}
min=0x7fffffff;
for(int i=1;i<=n;i++)//穷举医院建在N个结点,找出最短距离
{
total=0;
for(int j=1;j<=n;j++)
total+=g[i][j]*a[j];
if(total<min)min=total;
}
printf("%d",min);
return 0;
}4.题目:邮递员送信

输入:
5 10
2 3 5
1 5 5
3 5 6
1 2 8
1 3 8
5 3 4
4 1 8
4 5 3
3 5 6
5 4 2输出:
83注意:要判断重边如果输入了1 4 5和1 4 3就要有最小值,a[x][y]=min(a[x][y],z)!
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N][N];
int sum=0;
int n,m;
int main() {
cin>>n>>m; //n个地方,m条路线
memset(a,1e4+5,sizeof(a));
int x,y,z;
for(int i = 1; i <=m; i ++) { //m条路线的距离
cin>>x>>y>>z;
a[x][y]=min(a[x][y],z);
}
for(int k=1; k<=n; k++) { //这三个循环是Floyd-Warshall算法的核心代码
for(int i=1; i<=n; i++) { //a[i][j]表示i到j的最短距离
for(int j=1; j<=n; j++) { //意思是从i出发,经过k,然后到达j。
a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
}
}
}
for(int i=2; i<=n; i++)
sum+=a[1][i]+a[i][1];
printf("%d",sum);
return 0;
}




















 855
855











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








