Maple 第四章 表达式的处理和化简 (4.2有理分式)

一个有理分式通常可以写成两个多项式的商f/g,其中g是非零多项式.

对于有理分式,可以使用numer和denom命令分别求出有理分式的分子和分母

与有理数的计算不同的是Maple不会自动化简有理分式.只有当Maple能立即识别公因式时候,才能自动消去公因式

但是,新版本的Maple是可以自动化简的,如下图中所示,但这也可能会给计算带来麻烦,比如可能会忽略掉某些情况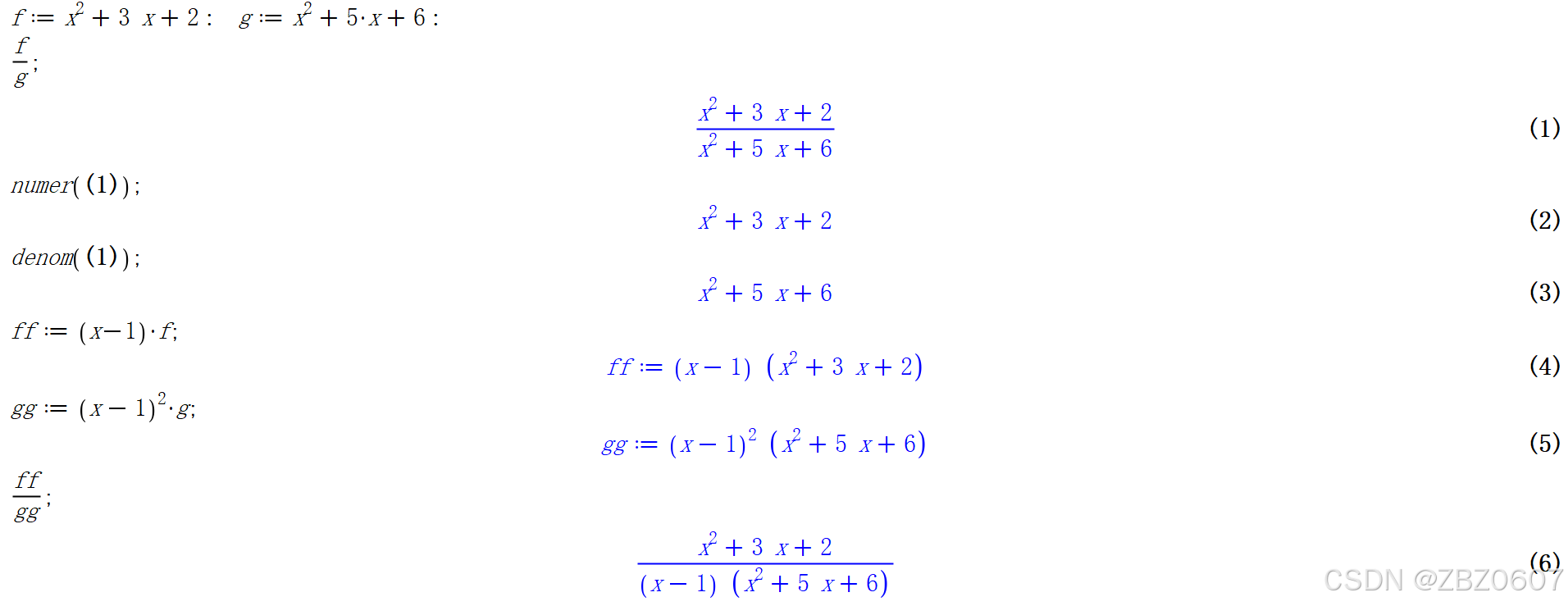

对于消去分子和分母的公因式的方法有两种,一个是使用命令factor(这个在上一节中也有所介绍)这个方法可以同时将分子分母的多项式分解因式,然后Maple回自动消去分子分母的公因式

另一种方法是使用normal命令,它的作用是将有理分式转化为规范形式.这个过程包括以下几个步骤:首先对于一个包含分式的表达式进行通分,转换成一个大分式,然后消去分子和分母中的公因式,从而得到较简单的表达式。normal命令一般将分子展开,不展开分母,如果想要normal也展开分母的话,可以用他的第二个参数expanded.

另外normal命令还可以递归地作用于函数、集合和列表上。

由上面的最后一个例子可以看出，normal命令不知道如何化简三角表达式,这次终于不是新版本解决掉得问题了.仅仅对有利函数有效.

既然normal命令有如此多的功能,Maple为什么不将有理分式自动化简为规范形式?原因有三:

1)有理分式的规范形式未必是最简的形式,例如(x^100-1)/(x-1)的规范形式就将包含100项

2)将有理分式化为规范形式将耗费Maple许多时间

3)用户有时需要对有理分式进行其他处理,例如分解为部分分式

在有限域和代数扩域上同样可以计算有理分式的规范形式,此时应当使用Normal命令,在有限域上计算规范形式的方法是Normal(a)mod p.其中a是有理分式,p是素数为有限域的特征.在代数域上计算有理分式的规范形式则需要使用evala命令.

对于有理分式也可以使用expand命令,它的作用是展开有理分式的分子

通常认为有理表达式在分母上没有分数指数的形式比较好.ration-alize命令通过有理式的分子和分母同时乘一个适当的因子来去除其分母上的根式

通常有理化后的结果比原来要长