大学物理期末复习知识点

01 高斯定理

性质

静电学中的高斯定理

• 描述了电场强度通过任意闭合曲面的通量等于该闭合曲面内所有电荷的代数和除以真空介电常数 ε0​ 。
• 表明静电场是有源场，电场线的起点和终点分别是正电荷和负电荷

磁场学中的高斯定理

• 指出通过任意闭合曲面的磁通量总是为零。
• 表明磁场是无源场，磁感线总是闭合曲线，没有独立的磁单极子

公式表示

静电学

• 
• 其中， ​ 是电通量，是电场强度，  是面元， ρ 是电荷密度， V 是闭合曲面 S 所包围的体积
• 

磁场学

• 
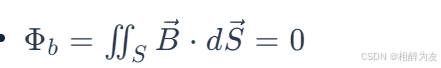
• 其中， Φb​ 是磁通量，  是磁感应强度

应用

计算电场强度

• 对于具有高度对称性的电荷分布（如均匀带电球体、无限大均匀带电平面等），可以使用高斯定理简便地计算电场强度

检验库仑定律

• 通过测定导体内部是否有净电荷，可以检验库仑定律的正确性

研究磁场特性

• 高斯定理在磁场学中的应用有助于理解磁场的无源性和磁感线的闭合特性

 

02 静电场环路定理

在静电场中，电场强度沿任意闭合路径的线积分等于零

这表明静电场是一个保守场，即电场力做功与路径无关，只与起点和终点的位置有关

 

03 磁感应强度计算

弧形导线产生的磁感应强度：

直线导线对特定点的磁感应强度：

无限长使用安培环路定律来计算：

有限长可用比奥-萨伐尔定律：

不能用安培环路~

θ1​ 和 θ2​ 是导线两端与观察点连线和导线之间的夹角

04 感应电动势的计算

法拉第电磁感应定律：

动生电动势：E=BLvsin(θ)

B 是磁感应强度， L 是导体长度， v 是导体运动速度， θ 是速度方向与磁场方向的夹角

感生电动势：

当磁场随时间变化时，即使导体静止，闭合电路中也会产生感应电动势。这种情况下，感应电动势的大小与磁场变化率成正比

交流发电机最大感应电动势：

其中 n 是线圈匝数， B 是磁感应强度， S 是线圈面积， ω 是角速度