一、逻辑回归基本介绍
逻辑回归是一种用于解决分类问题的统计学习方法,尽管其名称包含 “回归”,但实际用于处理因变量为二分类或多分类的场景(最常见的是二分类问题,如 “是 / 否”“0/1”)。它通过构建模型来预测样本属于某个类别的概率,进而实现分类。
1.1 核心原理
1.1.1. 线性回归的延伸
逻辑回归基于线性回归模型:,也可写成
,通过逻辑函数(Sigmoid函数)将线性输出映射到概率值[0,1]之间。
Sigmoid函数:
函数图像呈“S”型,当z趋近于正无穷时,σ(z)趋近于1;当z趋近于负无穷时,σ(z)趋近于0。
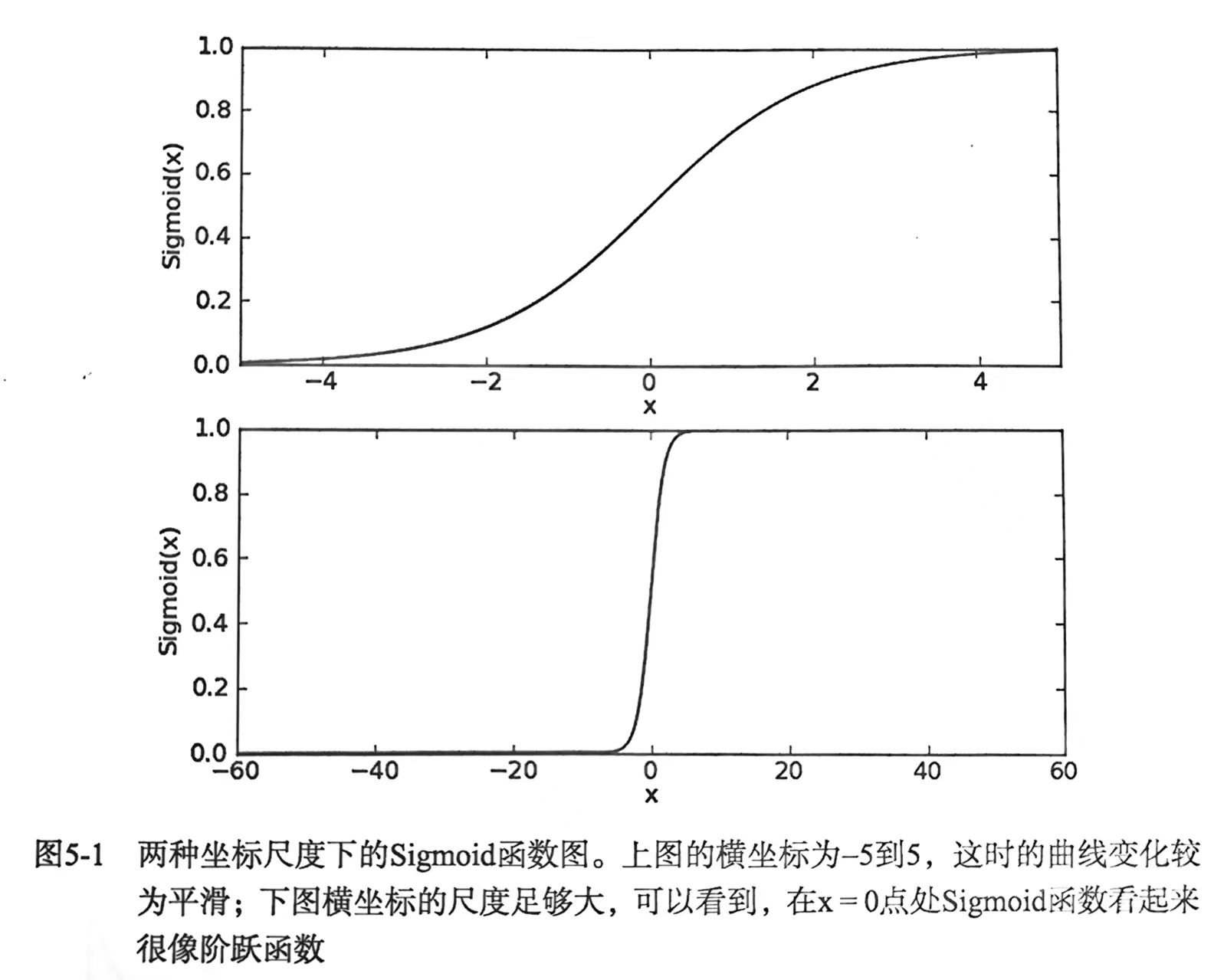
1.1.2.概率与分类决策
对于二分类问题(如正类“1”和负类“0”),模型输出样本属于正类的概率P(y=1|x) = σ(z),属于负类的概率为P(y=0|x) = 1 - g(z)。
分类阈值:通常设定阈值为0.5,若P(y=1|x) ≥ 0.5,则预测为正类,否则为负类。
1.2 数学模型与参数估计
1.2.1 二分类逻辑回归模型
设样本特征为 x = (x1,x2,...,xn),参数为 θ = (θ1,θ2,...,θn),则有:
,
合并表示为:
1.2.2. 参数估计:极大似然估计(MLE)
通过最大化样本的似然函数来求解参数θ。对数似然函数为:

通常使用梯度上升法或其优化变体(如牛顿法、拟牛顿法)求解最优参数。
1.3 适用场景
二分类问题:医学诊断(如是否患病)、金融风控(如是否违约)、垃圾邮件分类等。
多分类问题:可通过“一对多”(One-vs-Rest)或“多分类逻辑回归”(Softmax回归)扩展到多类别场景(如手写数字识别)。
1.4 与线性回归的区别
| 逻辑回归 | 线性回归 |
|---|---|
| 用于分类问题 | 用于回归问题 |
| 因变量为离散型(如 0/1) | 因变量为连续型(如房价、温度) |
| 通过 Sigmoid 函数映射到概率 | 直接输出连续值 |
| 损失函数为交叉熵损失,也称为对数损失(Log Loss) | 损失函数为均方误差(MSE) |
| 可以用梯度上升法直接最大化对数似然函数,但通常选择用梯度下降法最小化交叉熵损失 | 用梯度下降法最小化损失函数 |
二、逻辑回归的优化目标
2.1 损失函数
损失函数(Loss Function)是机器学习中用于衡量模型预测结果与真实标签之间差异的函数,本质上是对 “预测错误程度” 的量化。它是模型优化的核心目标,直接决定了模型训练的方向(如最小化损失或最大化收益)。
核心作用:
1. 量化误差:将预测值与真实值的差异转化为具体数值,便于数学优化。
例如:真实标签 y = 1,模型预测 y = 0.8,损失函数计算两者的差异(如交叉熵为-log(0.8) ≈ 0.223)。
2. 指导模型学习:通过损失函数的梯度(导数)反向传播,调整模型参数,使损失逐渐降低。
3. 评估模型性能:不同损失函数反映不同的优化目标(如回归注重数值误差,分类注重概率准确性)。
2.2 均方误差
线性回归最常用的损失函数为均方误差(MSE),定义为:

其中:
是模型预测值;
是第 i 个样本的真实值;
m 是样本数量;
θ 是模型参数(权重和偏置)。
线性回归之所以选择均方误差,是因为:
1.MSE是关于参数 θ 的凸函数,保证了全局最优解的存在性;
2.若误差项服从高斯分布,MSE等价于极大似然估计(MLE);
3.计算梯度时导数形式简洁,便于优化。
MSE关于参数 的梯度为:

2.3 交叉熵
在逻辑回归中,模型通过最大化训练数据的似然函数来估计参数。由于直接最大化似然函数在数学上不方便处理,通常会最小化负的对数似然函数,也称为交叉熵损失。
对于二分类问题(标签 y ∈ {0,1} ),逻辑回归通过Sigmoid函数将线性输出转换为概率:
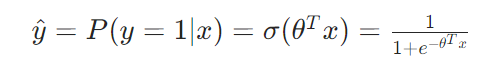
单个样本的交叉熵损失为:

- 当真实标签 y = 1 时,损失为
,若模型预测概率
接近 1,损失趋近于 0;若
接近 0,损失趋向无穷大;
- 当真实标签 y = 0 时,损失为
,若模型预测概率
接近 0,损失趋近于 0;若
接近 1,损失趋向无穷大。
整体的交叉熵损失函数为(m个样本的平均):

极大似然估计的目标是最大化 L(θ),而交叉熵损失函数 J(θ) = -L(θ)/m 正是对数似然的负值取平均,因此最小化交叉熵等价于最大化对数似然。
逻辑回归之所以选择交叉熵,是因为:
1. 交叉熵损失是关于参数 θ 的凸函数,保证了全局最优解的存在性;而 MSE 对于Sigmoid 函数是非凸的,存在多个局部最优解,梯度下降可能陷入局部极小值;
2. 梯度形式简洁,便于高效计算:

3. 交叉熵对错误预测的惩罚是指数级的,从而迫使模型对 “确信的错误” 进行更大幅度的参数调整。
三、优化算法
3.1 梯度下降法
梯度下降(Gradient Descent)是一种优化算法,用于寻找函数的局部最小值。在机器学习中,它是训练模型(如线性回归、逻辑回归、神经网络)最常用的优化方法之一,通过迭代更新模型参数来最小化损失函数。
3.1.1 核心思想与数学原理
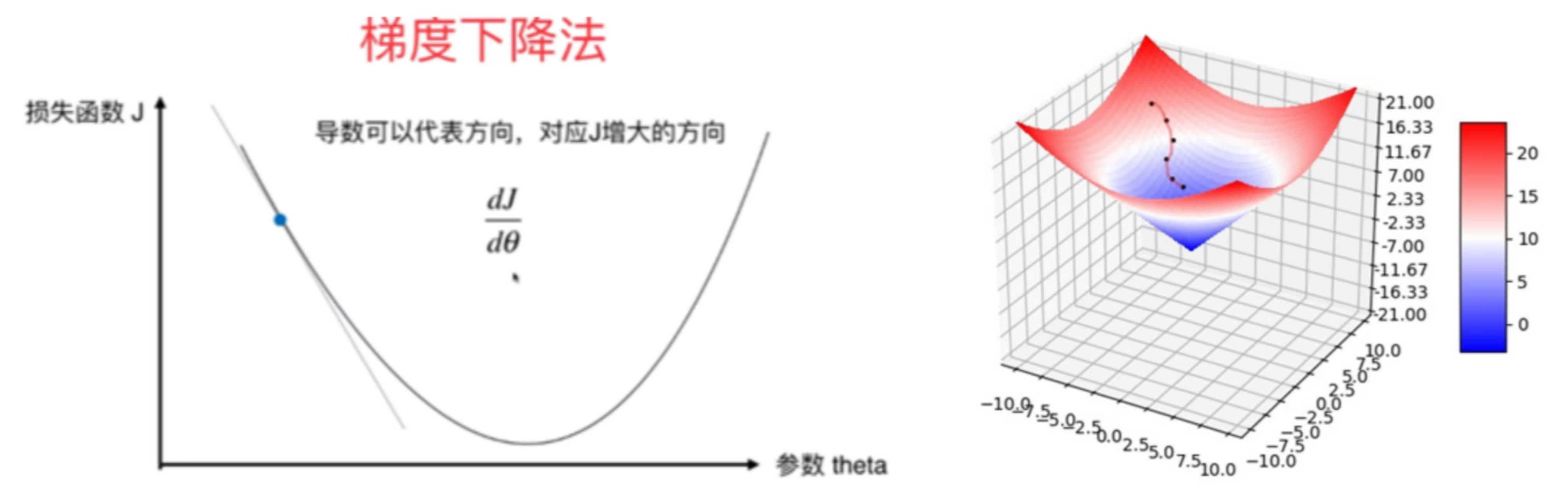
梯度下降的基本思想可以用 “下山” 来比喻:
假设你站在一座山上,想要最快到达山脚(最小值点),每一步,你选择当前位置下降最快的方向(即梯度的反方向)前进一小步,重复这个过程,直到无法继续下降(接近最小值点)。
数学原理:
对于函数 J(θ),其在点 θ 处的梯度 ▽J(θ) 指向函数值增长最快的方向。因此,梯度的反方向就是函数值下降最快的方向。
3.1.2 数学公式与迭代过程
梯度下降的参数更新公式为:θ = θ - α * ▽J(θ)
其中:
θ 是模型参数(如线性回归中的权重和偏置);
α 是学习率(Learning Rate),控制每次更新的步长;
▽J(θ) 是损失函数 J(θ) 关于参数 θ 的梯度。
迭代过程:
1. 初始化参数 θ (通常为随机值或全零);
2.计算当前参数下的梯度 ▽J(θ) ;
3.沿梯度反方向更新参数:θ ← θ - α * ▽J(θ) ;
4.重复步骤2-3直到满足收敛条件(如梯度接近零、损失变化小于阈值、达到最大迭代次数)。
3.1.3 学习率的影响
学习率 α 是梯度下降的关键超参数,其选择直接影响算法的收敛性:
学习率过大:参数更新步长过大,可能导致跳过最小值点,甚至发散(损失函数值不断增大);
学习率过小:参数更新步长过小,收敛速度极慢,需要更多迭代才能达到最小值。
3.1.4 应用场景与局限性
适用场景:
损失函数可导:梯度下降依赖于计算梯度,因此要求损失函数可微;
大规模优化问题:尤其适用于参数众多的模型(如神经网络);
局限性:
对于非凸函数,可能陷入局部最小值而非全局最优;
在高维空间中,梯度为零的鞍点可能导致算法停滞;
在深度神经网络中,梯度可能变得极小或极大,导致训练困难。
3.2 梯度上升法
梯度上升法(Gradient Ascent)是一种优化算法,用于寻找函数的局部最大值。也是训练模型(如极大似然估计、强化学习(策略梯度))的常用优化方法,通过迭代更新模型参数来最大化目标函数。
3.2.1 核心思想与数学原理
梯度上升的核心思想可以用 “爬山” 来比喻:
假设你站在一座山上,想要最快到达山顶(最大值点),每一步,你选择当前位置上升最快的方向(即梯度方向)前进一小步,重复这个过程,直到无法继续上升(接近山顶)。
数学原理:
对于目标函数 f(θ),其在点 θ 处的梯度 ▽f(θ) 指向函数值增长最快的方向。因此,梯度方向就是函数值上升最快的方向。
3.2.2 数学公式与迭代过程
梯度上升的参数更新公式为:θ = θ + α * ▽f(θ)
迭代过程:
1. 初始化参数 θ (通常为随机值或全零);
2.计算当前参数下的梯度 ▽f(θ) ;
3.沿梯度反方向更新参数:θ ← θ + α * ▽f(θ) ;
4.重复步骤2-3直到满足收敛条件(如梯度接近零、损失变化小于阈值、达到最大迭代次数)。
3.2.3 学习率的影响
学习率过大:参数更新步长过大,会导致参数震荡或发散;
学习率过小:参数更新步长过小,会导致收敛缓慢。
3.2.4 应用场景与局限性
适用场景:
极大似然估计(MLE):最大化对数似然函数估计模型参数,如逻辑回归、高斯混合模型;
强化学习(策略梯度):最大化累积奖励函数,优化策略网络参数;
对抗生成网络(GANs):判别器网络通过梯度上升最大化判别准确率;
局限性:
对于非凸函数,可能陷入局部最大值而非全局最优;
对于复杂函数,梯度可能在某些区域变得非常大或非常小,需进行梯度缩放或归一化。
四、示例:利用给定数据集完成逻辑回归
4.1 数据加载与预处理
给定数据集:

从文件加载数据集,提取特征矩阵 X 和标签向量 y。文件为制表符分隔的文本,共包含100个样例,文本前两列为特征值,最后一列是标签(0/1),即所属类别。
4.2 自定义逻辑回归实现
1. 初始化参数
学习率:控制梯度下降时参数更新的步长,自定义设置(我将其设置为0.1);
最大迭代次数:自定义设置(我设置为10000),防止算法无限循环。
收敛阈值:自定义设置(我设置为1e-4),当梯度的范数小于设置值时,认为算法已收敛。
参数向量:存储模型的权重和偏置,初始化为 None。
2. 调用sigmoid函数,将线性输出转换为概率值(0-1之间)
3.模型训练
添加偏置项:将输入特征矩阵X扩展为X_b,在第一列插入全 1 向量,对应偏置参数;
线性组合与概率转换:,h = σ(z)得到预测概率;
梯度计算:利用numpy库里的dot函数计算梯度(向量化实现),再用梯度下降法更新参数。
4.预测概率
添加偏置项,计算线性组合 ,通过 Sigmoid 函数转换为概率。
5.类别预测
根据预测概率和阈值将样本分类为 0 或 1,例如:若 prob = 0.65,则prob ≥ 0.5,为True,转换为整数1。
4.3 可视化数据集与决策边界
使用 meshgrid生成网格点,覆盖特征空间,通过 predict_prob计算每个网格点的预测概率,使用 contour绘制概率为 0.5 的等高线(即决策边界),使用 contourf填充不同概率区域,增强可视化效果。
4.4 模型训练对比
调用前面的自定义逻辑回归,用给定数据集训练模型,并存储模型的参数(包括偏置项和特征权重),再使用 scikit-learn 库中的 LogisticRegression类训练模型,存储模型的参数,作为对比基准,将参数对比输出,验证自定义逻辑回归的正确性。
4.5 代码实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#加载数据集
def load_data(file_path):
data = np.loadtxt(file_path, delimiter='\t')
X = data[:, :-1] #特征
y = data[:, -1].astype(int) #标签转为整数
return X, y
X, y = load_data('testSet(logistic).txt')
print("数据集大小:", X.shape[0], "样本")
#自定义逻辑回归类
class LogisticRegressionCustom:
def __init__(self, learning_rate=0.1, max_iter=10000, tol=1e-4):
self.learning_rate = learning_rate
self.max_iter = max_iter
self.tol = tol
self.theta = None
def sigmoid(self, z):
return 1 / (1 + np.exp(-z))
def fit(self, X, y):
m, n = X.shape
X_b = np.c_[np.ones((m, 1)), X]
self.theta = np.zeros(n + 1)
for iter in range(self.max_iter):
z = np.dot(X_b, self.theta)
h = self.sigmoid(z)
gradient = np.dot(X_b.T, (h - y)) / m
self.theta -= self.learning_rate * gradient
if np.linalg.norm(gradient) < self.tol:
print(f"迭代 {iter + 1} 收敛")
break
print(f"训练完成,迭代次数: {iter + 1}")
def predict_prob(self, X):
X_b = np.c_[np.ones((X.shape[0], 1)), X]
return self.sigmoid(np.dot(X_b, self.theta))
def predict(self, X, threshold=0.5):
prob = self.predict_prob(X)
return (prob >= threshold).astype(int)
#数据可视化及决策边界绘制
def plot_data_with_boundary(X, y, model):
plt.figure(figsize=(10, 6))
#绘制类别分布
scatter_0 = plt.scatter(X[y == 0, 0], X[y == 0, 1], color='red', marker='o', label='类别0')
scatter_1 = plt.scatter(X[y == 1, 0], X[y == 1, 1], color='green', marker='s', label='类别1')
#生成网格点并绘制决策边界
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100), np.linspace(y_min, y_max, 100))
#预测网格点概率并绘制阈值边界
Z = model.predict_prob(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
#绘制概率等高线(阈值0.5)
plt.contour(xx, yy, Z, levels=[0.5], colors='black', linewidths=2, linestyles='--')
#填充概率区域
plt.contourf(xx, yy, Z, levels=[0, 0.5, 1], colors=['lightcoral', 'lightblue'], alpha=0.3)
plt.xlabel('特征1')
plt.ylabel('特征2')
#手动构建handles来添加图例
handles = [scatter_0, scatter_1, plt.Line2D([], [], color='black', linestyle='--', label='Decision Boundary')]
plt.legend(handles=handles)
plt.title('类别分布与决策边界(阈值=0.5)')
plt.grid(True)
plt.show()
#训练模型
model = LogisticRegressionCustom(learning_rate=0.1, max_iter=10000)
model.fit(X, y)
#绘制合并图形
plot_data_with_boundary(X, y, model)
#对比scikit-learn模型
model_sk = LogisticRegression(max_iter=10000)
model_sk.fit(X, y)
print("\n自定义模型参数:", model.theta)
print("scikit-learn模型参数:", np.r_[model_sk.intercept_, model_sk.coef_[0]])运行测试结果截图:
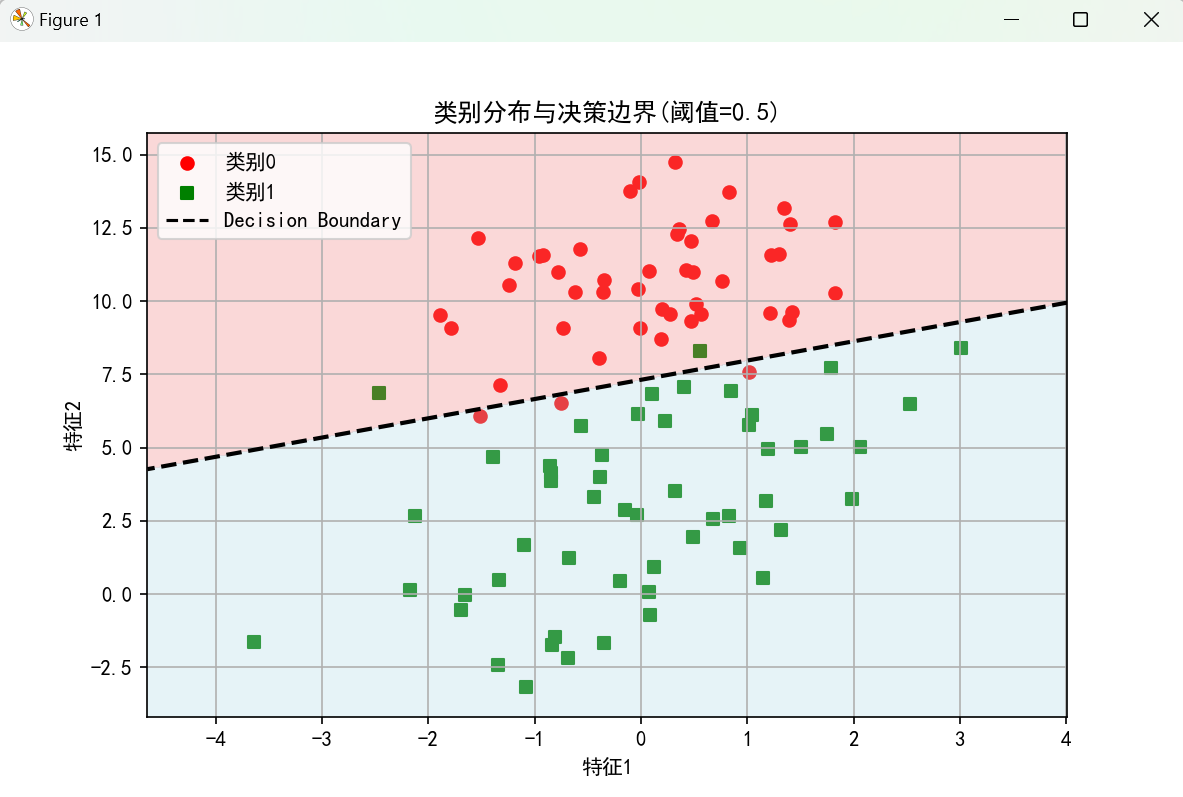

ps:更改学习率和迭代次数,模型参数值都会发生变化。
五、实验小结
优点:①计算高效:逻辑回归的训练和预测速度都非常快,因为只需要进行线性计算和 Sigmoid 转换,复杂度为 O(n);②可解释性强:逻辑回归的权重直接对应每个特征的重要性,正负号表示特征与类别之间的正相关或负相关关系;③不容易过拟合:通过正则化,可以有效防止过拟合,提高模型的泛化能力。
缺点:①对异常值敏感:由于使用对数损失函数,异常值可能对模型参数产生较大影响,需要进行数据预处理;②容易欠拟合,分类精度可能不高;
逻辑回归通过可视化权重,可以直观地看出哪些特征对预测最为重要,这在某些实际应用中非常重要(例如医学诊断);如果数据集中存在复杂的非线性关系,逻辑回归的表现会明显下降,此时应考虑使用非线性模型;可以尝试不同的学习率和迭代次数,以找到最优的训练参数。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








