一、分类模型的性能度量
分类模型的性能度量是用于评估分类算法预测效果的一系列指标和方法,它们帮助量化模型在不同方面的表现(如准确性、可靠性、泛化能力等)。
基础的分类指标:错误率和精度、精确率(Precision,查准率)和召回率(Recall,查全率)。
概率与阈值相关指标:PR曲线、ROC曲线与AUC。
二、PR曲线
PR曲线(Precision-Recall Curve)是一种用于评估分类模型性能的曲线,特别适用于类别不平衡的场景。它以精确率(Precision)为纵轴,召回率(Recall)为横轴,通过调整分类阈值(Threshold)来绘制曲线,直观反映模型在不同阈值下的表现。
2.1 混淆矩阵
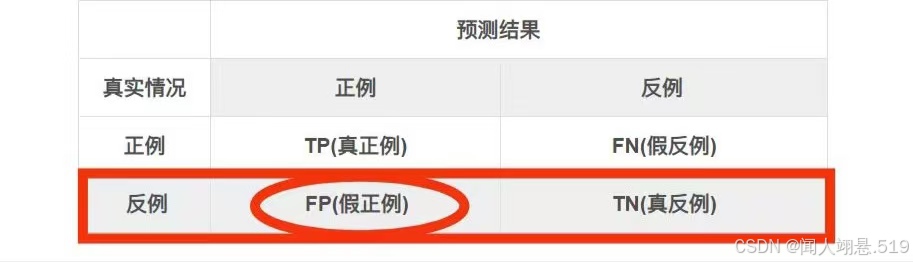
混淆矩阵(Confusion Matrix)是分类模型性能评估的核心工具,它以表格形式直观展示模型的预测结果与真实标签的对应关系,尤其适用于二分类和多分类问题。通过分析矩阵中的数值,可以计算准确率、精确率、召回率等关键指标。
| 预测结果 | |||
|---|---|---|---|
| 真实情况 | 正例 | 反例 | |
| 正例 | TP(真正例) | FN(假反例) | |
| 反例 | FP(假正例) | TN(真反例) | |
TP: 实际为正例,预测为正例的个数;
FN: 实际为正例,预测为反例的个数;
FP: 实际为反例,预测为正例的个数;
TN: 实际为反例,预测为反例的个数。
2.2 精确率(Precision)
精确率(又称查准率),是预测为正例的样本中真实为正例的比例,它特别关注预测结果的准确性,而非覆盖范围。
计算公式:

2.3 召回率(Recall)
召回率(又称查全率或灵敏度)用于衡量模型找出所有真实正例的能力。即实际为正例的样本中预测结果为正例的比例。
计算公式:

2.4 PR曲线的绘制步骤
1. 数据准备阶段
数据集选择:选择一个二分类数据集,确保数据包含特征和标签(正例/反例);
数据分割:将数据集分为训练集(70%~80%)和测试集(20%~30%),确保测试集具有代表性。
2. 训练KNN分类器
模型初始化:设置KNN的参数;
训练模型:用训练集拟合模型。
3. 获取预测概率
获取模型对正类的预测概率(非硬分类结果),调用predict_proba()方法获取。
4. 计算精确率与召回率
将概率(最高到最低)逐个设置为当前阈值,在每个阈值下对样本进行划分:大于当前阈值的为预测成正例的个数,小于当前阈值的为预测成反例的个数,从而得到多个混淆矩阵,计算不同阈值所对应的精确率和召回率。
5.绘制PR曲线
以精确率为纵轴,召回率为横轴,将每个阈值下对应的精确率和召回率作为坐标点一一标出,然后用平滑的曲线连接这些坐标点,就绘制得到PR曲线。
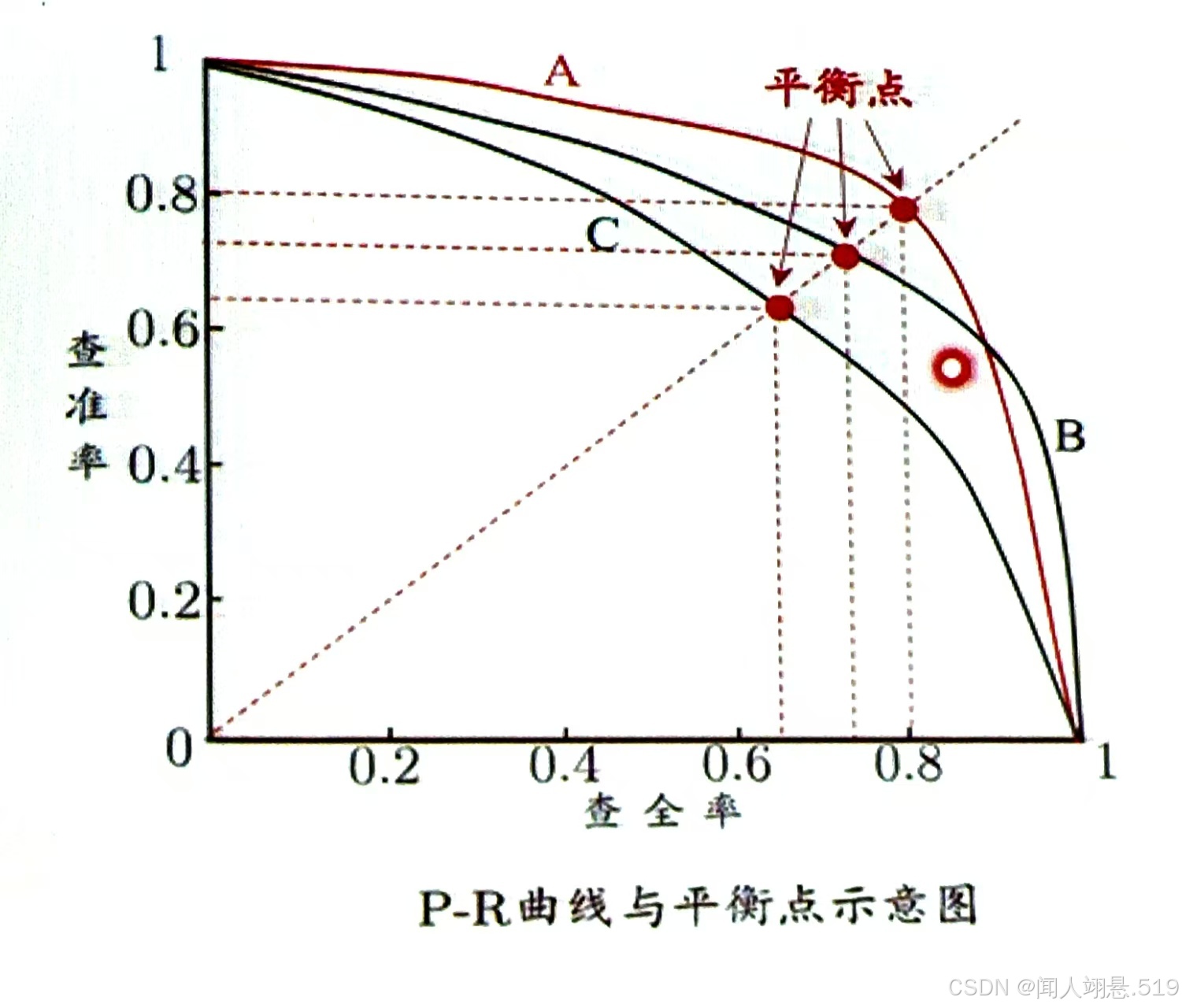
平衡点(BEP)是曲线上“精确率(查准率) = 召回率(查全率)”时的取值,可用于度量PR曲线有交叉的分类器的性能高低。
(1)PR曲线下的面积越大,则性能越好;
(2)若某个分类器的PR曲线被另一个分类器的PR曲线包住,则后者性能优于前者,例如图中 A和B的性能优于C;
(3)若分类器的PR曲线交叉,则通过平衡点进行判断,如果分类器的BEP值较大,说明该分类器的性能较好,所以PR曲线越靠近右上角性能越好,例如图中A的性能优于B。
三、ROC曲线与AUC
ROC曲线(Receiver Operating Characteristic Curve)是用于评估二分类模型性能的常用曲线,它以真正例率(TPR)为纵轴,假正例率(FPR)为横轴,通过描绘模型在不同阈值下的真正例率和假正例率的关系,直观反映模型的判别能力。
3.1 真正例率(True Positive Rate)
真正例率用于衡量模型正确识别正例样本的能力,即实际为正例的样本中预测结果为正例的比例。
计算公式:

3.2 假正例率(False Positive Rate)
假正例率用于衡量模型将反例样本错误预测为正例的能力,即实际为反例的样本中预测结果为正例的比例。
计算公式:
3.3 ROC曲线的绘制步骤
1. 数据准备阶段
数据集选择:选择一个二分类数据集,确保数据包含特征和标签(正例/反例);
数据分割:将数据集分为训练集(70%~80%)和测试集(20%~30%),确保测试集具有代表性。
2. 训练KNN分类器
模型初始化:设置KNN的参数;
训练模型:用训练集拟合模型。
3. 获取预测概率
获取模型对正类的预测概率(非硬分类结果),调用predict_proba()方法获取。
4. 计算真正例率和假正例率
将概率(最高到最低)逐个设置为当前阈值,在每个阈值下对样本进行划分:大于当前阈值的为预测成正例的个数,小于当前阈值的为预测成反例的个数,从而得到多个混淆矩阵,计算不同阈值所对应的真正例率和假正例率。
5.绘制ROC曲线
以真正例率为纵轴,假正例率为横轴,将每个阈值下对应的真正例率和假正例率作为坐标点一一标出,然后用平滑的曲线连接这些坐标点,就绘制得到ROC曲线。
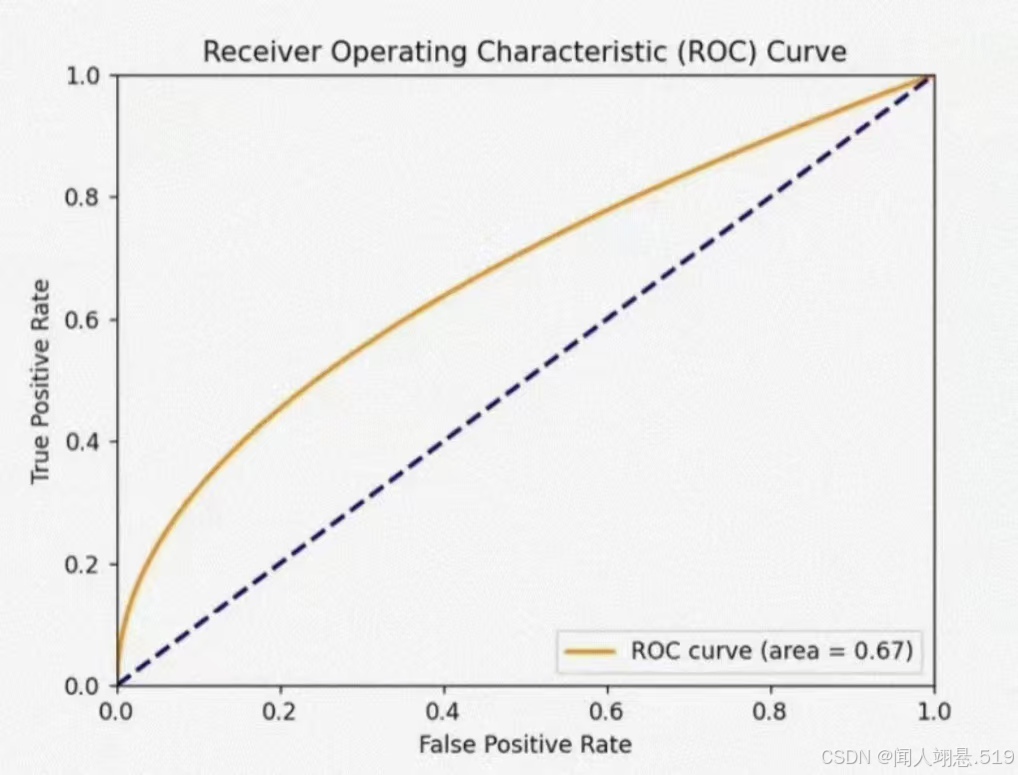
3.4 ROC AUC
ROC AUC表示ROC曲线下的面积,用于量化模型区分正反类样本的整体能力。其值范围在0.5(随机猜测)到1(完美分类)之间,越接近1说明模型性能越好。
假设ROC曲线∈{(x1,y1),(x2,y2),...,(xm,ym)}的点按序连接而成(x1=0,xm=1)
则AUC的计算公式:


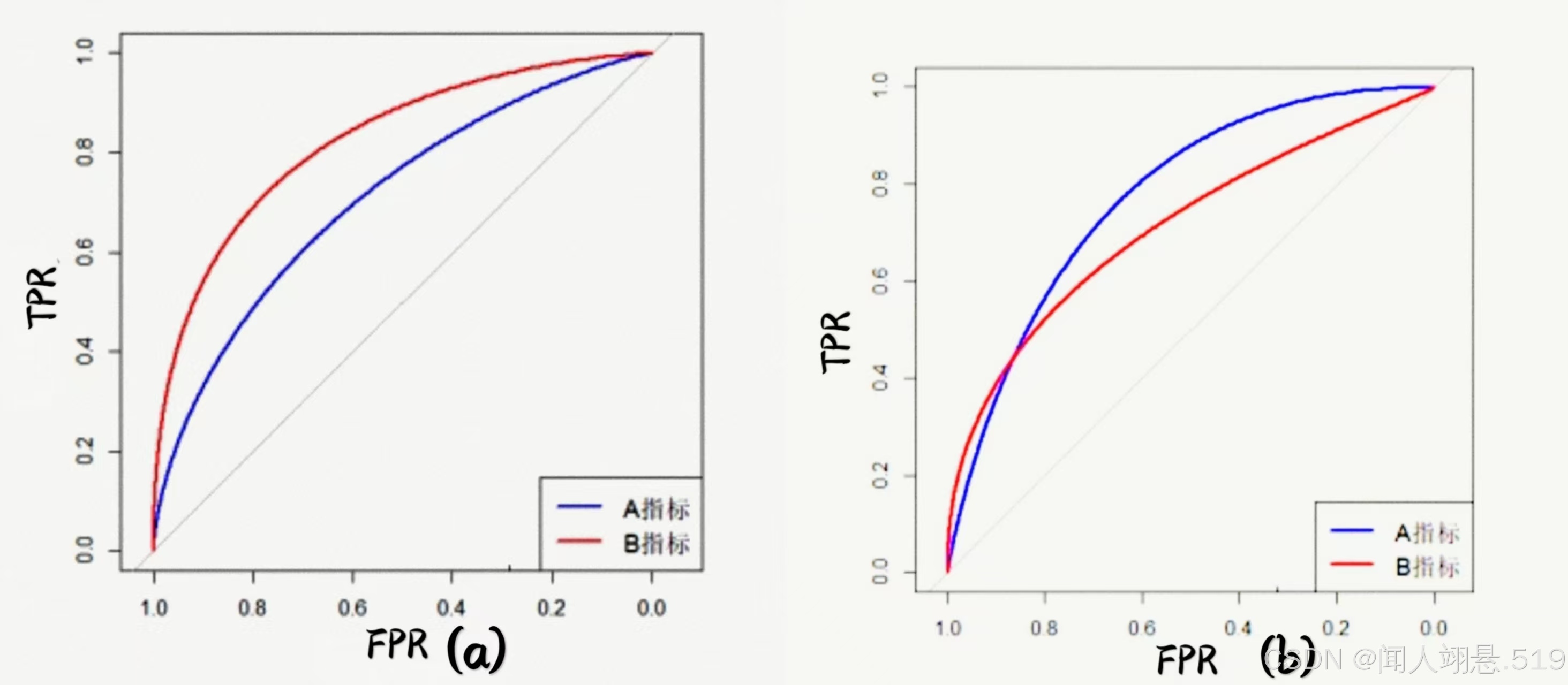
(1)若某个分类器的ROC曲线被另一个分类器的ROC曲线包住,则后者性能优于前者,例如图(a)中A的性能优于B;
(2)如果曲线交叉,则可以通过ROC AUC值进行比较,ROC AUC的值越大,则性能越好,例如图(b)中需要计算A和B的AUC值再比较;
(3)如果某个分类器的ROC曲线低于平衡线,则几乎没有存在的必要;
(4)曲线上的点表示对应假正例率下的最大真正例率,因此ROC曲线越靠近左上角性能越好。
四、代码实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import precision_recall_curve,roc_curve,auc
#第一次使用sklearn需要用命令pip install scikit-learn或py -m pip install scikit-learn进行安装
#随机数据生成
def create_data():
X, Y = make_classification(
n_samples = 5000, #生成的总样本数
n_features = 2, #每个样本的特征数量
n_classes = 2, #分类的类别数
n_informative = 2, #两个特征都具有信息量
n_redundant = 0, #无冗余特征
n_clusters_per_class = 2, #每个类别对应的聚类中心数量
random_state = 35
)
return X, Y
datas,labels = create_data()
#划分训练集和测试集
datas_train,datas_test,labels_train,labels_test = train_test_split(
datas,labels,test_size = 0.3,random_state = 35
)
#数据标准化(仅在训练集上fit,然后转换训练集和测试集)
scaler = StandardScaler()
datas_train = scaler.fit_transform(datas_train) #只在训练集上计算均值和方差
datas_test = scaler.transform(datas_test) #使用训练集的统计量转换测试集
#训练KNN模型(k = 5)
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(datas_train,labels_train)
#获取预测概率(正类的概率)
labels_scores = knn.predict_proba(datas_test)[:, 1]
#计算精确率与召回率(使用sklearn自动优化阈值)
precision,recall,thresholds = precision_recall_curve(labels_test,labels_scores)
pr_auc = auc(recall,precision) #计算AUC
#计算假正例率和真正例率
FPR,TPR,_ = roc_curve(labels_test,labels_scores)
roc_auc = auc(FPR,TPR) #计算AUC
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei'] #使用黑体显示中文
plt.rcParams['axes.unicode_minus'] = False #解决负号显示问题
#绘制双图
plt.figure(figsize=(11,5))
#绘制PR曲线
plt.subplot(1,2,1)
plt.plot(recall,precision,color='blue',lw=2,
label=f'PR curve (AUC = {pr_auc:.2f})')
#计算平衡点
#找到最接近 Precision = Recall 的点
diff = np.abs(precision - recall)
be_index = np.argmin(diff)
be_precision = precision[be_index]
be_recall = recall[be_index]
#标记平衡点
plt.scatter(be_recall,be_precision,color='red', s=40,
label=f'平衡点 (P=R={be_precision:.2f})')
plt.annotate(f'阈值={thresholds[be_index]:.2f}',
xy=(be_recall,be_precision),
xytext=(20,-30),
textcoords='offset points',
bbox=dict(boxstyle='round,pad=0.5',fc='white',alpha=0.8),
arrowprops=dict(arrowstyle="->"))
plt.xlabel('Recall(召回率)',fontsize=12)
plt.ylabel('Precision(精确率)',fontsize=12)
plt.title('PR曲线',fontsize=14)
plt.legend(loc='lower left')
#绘制ROC曲线
plt.subplot(1,2,2)
plt.plot(FPR,TPR,color='darkorange',lw=2,
label=f'ROC curve (AUC = {roc_auc:.2f})')
plt.plot([0, 1],[0, 1],'k--',lw=1) #随机猜测线
plt.xlabel('False Positive Rate(假正例率)',fontsize=12)
plt.ylabel('True Positive Rate(真正例率)',fontsize=12)
plt.title('ROC曲线',fontsize=14)
plt.legend(loc='lower right')
#显示图像
plt.tight_layout()
plt.show()
五、小结
1.数据标准化应该在训练集和测试集拆分之后进行,并且应该仅使用训练集的统计量来转换测试集,以避免数据泄露;
2.要将测试集上的训练误差作为泛化误差的近拟,因此测试集要和训练集的样本尽量互斥;
3.划分训练集和测试集的方法:留出法、交叉验证法等,本实验使用了k折(k = 5)交叉验证;
4.可以自定义规则随机生成数据(但数据简单,不能充分测试模型能力),可以调用make_classification生成更复杂、真实的分类数据;
make_classification包含多个参数,通过调整这些参数的数值,可以得到不同的绘制效果,例如若n_features = 2而n_informative = 1,那么第二个特征就是噪声;n_clusters_per_class = 1表示每个类别只有一个聚类簇(数据分布更集中),增加该值会使数据分布更复杂;random_state为随机种子,用于控制数据的可复现性,相同的random_state能保证后续使用train_test_split时得到相同的训练/测试集划分;
(random_state设置为固定值:每次生成完全相同的数据;None/不设置:每次运行生成不同的数据;不同固定值:生成不同但确定性的数据;虽然数据具体值会变,但n_informative等参数控制的核心特性(如特征相关性)会保持不变)
5.调用sklearn的内置方法precision_recall_curve,roc_curve函数自动计算得到参数指标,并且可以自动优化阈值;
6.PR曲线涉及到精确率计算,容易受到样本分布的影响,而ROC曲线对正负样本比例不敏感,可能掩盖模型在少数类上的表现,因此类别不平衡时PR曲线更可靠;
7.通过PR和ROC两种互补的评估曲线,可以全面了解模型在不同阈值下的表现,可用ROC AUC衡量模型区分能力,用PR AUC衡量正类预测精度。























 1693
1693

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








