每日一练：对称二叉树-CSDN博客

本文链接：https://blog.csdn.net/2303_78095330/article/details/142467583

一、题目要求

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

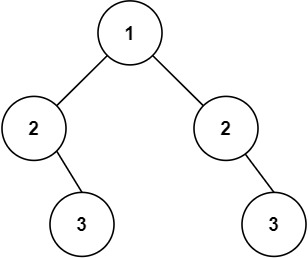
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

二、解法1-递归 O(N)

使用递归，从根开始比较左右两边的节点的val是否相同。

class Solution {
    bool _isSymmetric(TreeNode* left, TreeNode* right) {
        if (left == nullptr && right == nullptr) // 走到尾，都为空
            return true;
        if (left == nullptr && right != nullptr || // 一边走到尾，另外一般不是空
            right == nullptr && left != nullptr)
            return false;
        if (left->val != right->val) // 对称节点不相同
            return false;
        return _isSymmetric(left->left, right->right) &&
               _isSymmetric(left->right, right->left);
    }
public:
    bool isSymmetric(TreeNode* root) {
        if (!root)
            return true;
        return _isSymmetric(root->left, root->right);
    }
};

三、解法2-迭代 O(N)

迭代需要我们维护一个栈，每次循环查看栈顶的两个节点是否对称，如果对称且不为空，就插入这两个节点的四个子节点；如果为空说明走到尾了，就不插入。

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (!root)
            return true;
        stack<TreeNode*> s; // 栈
        s.push(root->left);
        s.push(root->right);
        while (!s.empty()) {
            TreeNode* root1 = s.top();
            s.pop();
            TreeNode* root2 = s.top();
            if (root1 == nullptr && root2 == nullptr) { // 为空不再插入节点
                s.pop();
                continue;
            }
            if (root1 == nullptr && root2 != nullptr ||
                root2 == nullptr && root1 != nullptr)   // 不对称
                return false;
            if (root1->val != root2->val) // 不对称
                return false;
            s.pop();
            s.push(root1->left);
            s.push(root2->right);
            s.push(root2->left);
            s.push(root1->right);
        }
        return true;
    }
};