2021年华为杯数学建模竞赛F题论文和代码

 COVID-19 疫情期间生活物资的科学管理问题

在疫情封闭式管理期间，生活物资的高效发放有助于减少人员接触，对疫情防控具有重要的意义。本文基于长春市疫情期间相关数据资料，分析了发放生活物资在疫情防控中的作用，对长春市生活物资发放方案进行了评价及优化，并制定了未来特殊时期保障居民生活物资供应的详细预案。

针对问题一，分析蔬菜包发放对疫情防控效果的影响。首先，我们将数据分为疫情严重时期和疫情后期两部分，对每个部分的新增感染者人数和发放蔬菜包数量计算斯皮尔曼相关系数从而进行相关性分析。然后，建立SIR模型预测了未发放蔬菜包情况下的感染者人数，将预测结果与现实情况进行对比。分析发现，及时高效地发放蔬菜包对疫情的发展起到了一定的抑制作用，有利于疫情防控。

针对问题二中的投放站数量分析以及优化的问题，在收集2020以及2021长春市统计年鉴数据的基础上，考虑了单位面积投放站数量、单个生活物资投放点服务人口数量、单个生活物资投放站日均发放蔬菜包重量以及单个生活物资投放站服务小区数量等指标以及长春市疫情防控物资发放中的打通最后一公里等相关政策，发现二道区投放点密度为0.0093个每平方千米，存在投放点数量较少的情况。绿园区平均每投放点服务小区数量仅为0.3106个，存在投放点数量过多、资源浪费的情况。根据上述指标建立优化模型对各个区投放站数量分布进行优化，并使用 Python+SCIP 求解器进行求解。得到9个区的投放站数量分别为朝阳区63个、南关区56个、宽城区76个、绿园区65个、二道区91个、长春新区65个、经开区62个、净月区55个、汽开区50个。优化后的投放站数量为583个，相比于优化前降低了63%。针对问题二中的储备物资和大规模物资分拣场所的选址，首先使用弗洛伊德算法求解交通网络图中的小区节点与路口节点的实际距离。在考虑建设成本等因素的基础上，建立了以运输距离最短、每个分拣场所服务人口均衡多目标优化问题模型，并使用遗传算法进行求解，得到最优储备物资和大规模物资分拣场所数量为7个并给出了相应的选址、覆盖小区数量、服务人口数量。通过调整优化目标权重，得到了3个备用储备物资和大规模物资分拣场所的选址。

针对问题三，分析蔬菜包需求和发放规律，评价并调整4月10日至 15日蔬菜包供应方案。首先，我们从蔬菜包需求量与发放量之间的关系与蔬菜包发放量和感染者人数之间的关系两个方面总结了蔬菜包需求-发放规律。然后，以蔬菜包投放量、人口密度、交通空间比例作为投入指标，新增感染人数作为产出指标，使用数据包络分析方法对4月10日至15日各区蔬菜包供应方案进行了对比评价，结果表明4月10日净月区、4月11日净月区、4月14日南关区、4月15日二道区、4月15日汽开区的蔬菜包发放数量最为合理，4月13 日宽城区的蔬菜包发放数量最不合理。最后，以各区域每日发放完蔬菜包后的库存量最小、各区域蔬菜包的发放成本之和最小、各区域蔬菜包人均需求量之间的极差最小作为优化目标，建立并求解多目标优化模型，对蔬菜包发放方案进行了优化调整。

针对问题四的生活物资供应的详细预案设计问题，在问题二的基础上，使用弗洛伊算法计算考虑人力权重以及实际道路距离下的成本权重矩阵。以最小化人力成本和与重要交通枢纽或道路之间的距离为目标建立上游各项物资来源地的选址优化问题并求解得到了9个上游各项物资来源地的位置以及附近的重要交通枢纽的情况。随后建立了人力成本最小化的中游物资集散地的位置最优选址优化问题，并使用遗传算法进行求解得到了9个区583个中游物资集散地的位置并给出了对应小区的集合。在上

一小问和第三问的基础上进一步考虑卡车配送物资，分析物资来源地一集散地一小区的蔬菜包存储量和发放量，建立了多层级储备中心集散区协同选址—配送模型，并使用了模拟退火遗传算法得到了各网络之间的物资分配、车辆分配以及最优选址结果。对比上一问得出的选址方案，进一步减少了中游集散地的数量，减少为494个，减少了车辆跨区操作和人力成本，降低了人员接触的机会。

关键字：斯皮尔曼相关系数 数据包络分析 遗传算法 模拟退火算法 多层级网络选址 弗洛伊德算法 整数规划

1 问题背景与问题重述

1.1 问题背景

2022年以来，全国报告新冠肺炎感染者人数显著增多，疫情呈现点多、面广、频发的特点，个别省份呈多链并行、隐匿传播、快速蔓延态势。目前，我国主要采取封闭式管理的方式实现新增感染人数的快速清零。在封闭式管理期间，居民生活物资的发放问题丞待解决。

疫情期间生活物资的管理和发放是一个涉及多区域、多部门的复杂系统工程[1]。相关数据表明，政府有能力调动足够的生活物资，只是生活物资的具体发放策略难以制定且发放渠道不畅，导致疫情初期存在一定程度的管理混乱，容易造成居民抢购生活物资而影响疫情防控的情况。因此，需要提前制定有效的生活物资管理方案来及时应对突发疫情。

蔬菜包作为一种以新鲜蔬菜为主的生活物资，对疫情期间居民的生活保障起到了重要的作用。但由于其具有保质期相对较短且需求量较大的特点，导致蔬菜包供应频繁，容易造成人员的大量接触，增大疫情感染风险。故本题要求对蔬菜包供应策略与疫情发展状况进行研究，根据相关数据资料建立模型，制定科学可行的蔬菜包供应方案，给今后的疫情防控工作提供参考。

1.2 问题重述

结合以上研究背景，以长春市本轮疫情为例，解决如下问题：

问题一：

根据长春市疫情期间每日新增感染人数数据(附件一) 及其他搜集到的数据对长春市发放蔬菜包前后的疫情防控效果进行判别和分析。

问题二：

结合长春市疫情期间每日生活物资相关数据(附件四) 与长春市各区交通网络和各小区位置等相关数据(附件三)，分析附件二中长春市不同区域投放点数量的合理性，并建立数学模型对其进行优化。此外，考虑未来疫情或自然灾害等特殊事件，合理规划政府储备物资和大规模物资分拣场所的最优选址数量、规模及其备用位置。

问题三：

参考长春市及各区疫情期间蔬菜包接收和方法数量(附件五)，分析蔬菜包需求和方法规律，并根据长春市各小区位置和人口信息(附件三)，评价并调整4月10日至15日期间长春市蔬菜包供应方案。

问题四：

在第二、三问的基础上，结合长春市街道和小区情况(附件三)，以有序网络图的形式提出疫情或自然灾害等特殊事件期间保障居民生活物资供应的详细预案，并考虑用卡车运送物资的情况下预案有无显著不同。

2 模型假设

1. 原始数据来源于官方网站真实数据，不存在误差。

2.疫情期间长春市处于相对封闭状态，不存在与外省市的人口流动。

3. 长春市每日蔬菜包总量固定。

4. 集散点到最近道路口的距离忽略不计。

3 符号说明

符号                        含义

 Prei              第i个区的集散点的数量(优化前)

V                     长春市9个区的集合

A₁                     第i个区的面积

P₁                    第i个区的小区数量

C₁               第i个区的日均蔬菜包发放数量

M₁                  第i个区的人口数量

N⁺                       正整数集

 Dkj              第k个小区到第j个路口的距离

H                  长春市1357个小区的集合

Q₂                 第k个小区的人口数量

⇔                  长春市9932个路口的集合

 Pij              第i天第j个区的蔬菜包需求量

 ris             第i天第j个区的蔬菜包实际发放量

8ij           第i天第j个区发放蔬菜包后的库存量

PP₂                    第j个区的人口数量

x; jt                j区在第t天执行第i个投入

 yrjt                j区在第t天第r个产出指标

μrjt            j区在第t天第r个产出的权重系数

 Vige            j区在第t天第i个投入权重系数

 att              j区在第t天第i个投入的松弛因子

878             j区在第t天第r个产出的松弛因子

θ                  目标函数的对偶变量

λ                       对偶系数

€                    非阿基米德无穷小量

V₀            小区i到路口j之间的人力成本矩阵

Y₀            小区i到路口j之间的人力成本矩阵

6

hé               第k个区上游集散点的位置向量

hé           第k个区的路口i是否被选为上游集散点

E*                  第k个区的路口集合

H'                   第k个区的小区集合

i*               第k个区中游集散点的位置向量

17          第k个区的路口i是否被选为中游集散点

qì          第k个区的路口i是否距离重要交通节点近

vǒ         第k个区的小区i到路口j之间的人力成本矩阵

 Lt         第k个区的小区i到路口j之间的匹配矩阵

 Cuj           路口i到路口j之间的最短距离矩阵

 Ctrl        第k个区的路口i到路口j之间的最短距离矩阵

 Cl ₂     第k个区的路口i到路口j之间的最短距离矩阵

I                      物资来源地集合

J                        集散地集合

K                       小区集合

N            运送物资从物资来源地到集散地的车辆集合

M              运送物资从集散地到小区的车辆集合

8:                 第i个物资来源地启用

第j个集散地启用

BTjk              第j个集散地覆盖第k个小区

xù        车辆n从第i个物资来源地运送物资至集散地j

yī           车辆m从第j个集散地运送物资至小区k

 Uni   车辆n从第i个物资来源地运送物资至集散地j 并且不返回

Vik     车辆m从第j个集散地运送物资至小区k并且不返回

d₁₂          物资来源地i至集散地j的运输距离

 djk               集散地j至小区k的运输距离

 qct               第t天c城区人均蔬菜发放量

RQ;                 第j个集散地的最大存储量

SR₁j       从第i个物资来源地运送至第j个集散地的蔬菜总量

LN₁        从物资来源地到集散地的单位车辆最大载重量

LN₂            从集散地到小区的单位车辆最大载重量

I₁              第t天全市总的蔬菜包发放量

B:                第t天全市总的蔬菜包接收量

4 问题一

4.1 问题分析

针对问题一，要求根据附件1中长春市疫情期间新增感染人数和附件5中发放蔬菜包情况，对长春市发放蔬菜包前后疫情状况进行判别和分析。首先，我们通过对蔬菜包的发放情况与疫情新增感染人数进行相关性分析，判断他们之间是否存在相关性。然后，建立传染病模型对未发放蔬菜包情况下的疫情情况进行预测，观察并比较其与现实发放蔬菜包情况下新增感染人数的区别，分析发放蔬菜包对疫情防控的作用。

4.2 问题求解

4.2.1 相关性分析

首先，对长春市此轮疫情期间病毒感染人数数据进行整理分析。附件一提供了3月4日至5月23日长春市每日新增无症状及本土感染者数量，如图4.1所示，从3月4日开始出现零星新增新冠疫情感染者，4月2日新增人数达到峰值3823人后逐渐减少，至5月9日新冠疫情新增人数基本清零。从图中可以看出，在4月13日左右新增本土感染者已降至100以下，但由于无症状感染者数量较多且难以排查，导致疫情仍继续持续了一个月左右。

根据附件5中疫情期间每日蔬菜包相关数据得知，长春市各区域从3月26日开始接收并发放蔬菜包。结合上述疫情发展情况可发现，在发放蔬菜包前，新增感染人数处于上升趋势：在发放蔬菜包后一周内，新增感染人数达到峰值并开始下降。由于病毒潜伏期的存在以及无症状感染者难以排查的原因，发放蔬菜包后经过一段延迟时间，新增感染人数才开始下降，因此，蔬菜包的发放可能与新增感染人数(疫情的发展趋势) 有一定的关联。

我们以发放蔬菜包时期(3月27日至5月1日)的数据作为样本，将附件5中每日发放蔬菜包数量和附件1中当日感染者人数之间的关系用散点图进行分析，观察发放蔬菜包数量和感染者人数之间是否存在线性关系，结果如下：

根据散点图可以发现，发放蔬菜包数量和感染者人数之间存在较强的线性关系。此外，发放蔬菜包时期的数据可以分为两部分：一部分为疫情较为严重时期(3月27日至4月15 日)，该时期发放蔬菜包数量和感染者人数之间存在一定的负相关关系如图4.3所示：另一部分为疫情缓解时期(4月16日至5月1日)，发放蔬菜包数量和感染者人数之间呈现正相关关系，如图4.4所示。

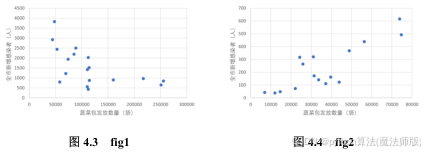
为了进一步研究并量化蔬菜包发放数量和感染者人数之间的关系，我们使用相关性分析对其之间的相关程度进行分析。通常相关分析的计算方式有两种，分别是皮尔逊( Pearson)相关系数和斯皮尔曼( Sperman)相关系数。由于样本的正态性检验结果表明其不满足正态分布，因此我们选择使用斯皮尔曼相关系数进行相关分析。斯皮尔曼相关系数计算公式如下：

 ρ=∑txi-xyi-y∑xj-x2∑1yi-y2                         (4.1)

其中ρ∈[-1，1]表示斯皮尔曼相关系数，其绝对值越接近于1时，表示两个变量之间相关性越强，ρ为正数时表示正相关，反之表示负相关。使用MATLAB计算得到两个变量之间的斯皮尔曼相关系数如下表所示：

表4.1   斯皮尔曼相关系数

时期	相关系数ρ	p值
3.27-4.15 4.16-5.1	-0.6058 0.7706	0.0090** 0.0007***

注: ***、**分别代表1%、5%的显著性水平(双尾)

由上表可知，在95%的显著性水平下，蔬菜包发放数量和新增感染人数存在相关性。在疫情上升且较为严重的时期，发放蔬菜包数量与新增感染者人数呈负相关，说明在疫情发生时及时有效地发放蔬菜包等生活物资可以有效减少人们自行外出购买而导致的人员接触聚集，降低病毒感染率，有助于对疫情的控制：在疫情受到控制逐渐缓解的时期，发放蔬菜包数量与新增感染者人数呈正相关，究其原因可能是由于疫情发展到后期，大部分被感染者已经被采取隔离等措施，由于流动的被感染者减少，政府不需再统一供应蔬菜包等生活物资。

4.2.2 SIR 传染病模型预测

为进一步观察长春市实行蔬菜包发放对疫情防控的影响，我们构建了一个 SIR传染病模型，观察在未实行蔬菜包发放政策下，本土感染病例与无症状感染病例的变化情况，并将预测结果与实行蔬菜包发放政策后的病例结果进行比较，得到蔬菜包发放对疫情防控的影响，最后对蔬菜包的发放给出相应的建议。

首先对模型进行假设，假设模型中总人数N不变； 假设感染率α与移除率β为常数：假设被隔离者与外界隔离后，不会进行传染：假设痊愈患者解除隔离后，不具备传染能力以及不会被再次感染；假设移除者中，死亡人群不具有感染性。根据模型分析，我们建立SIR模型常微分方程：

(4.2)

其中S₂表示t时刻的易感染人数，I₂表示t时刻的感染人数，R₁表示t时刻的移除人数，α为感染率，β为移除率。通过观察式(4.2) 可知，S₂为递减的函数，与常态化的疫情防控情况相符。当感染者 I₂开始递减时，我们可以获得以下方程：

 jc=fraenSiIkN-βIt=0.                          (4.3)

由于数据是以天为时间单位进行采集的，因此我们需要对上述模型进行离散化，离散后的系统状态方程如下：

(4.4)

利用 Matlab中的龙格-库塔法，求解上述离散状态方程，可以预测出下一天的易感染人群数量、感染者数量以及移除者数量。

通过式 (4.4)，我们可以看出，预测精度主要受感染率α和移除率β的影响。我们利用附件一的数据，收集3月4日至3月26日的本土感染者、痊愈患者以及易患病感染者的人数变化，将其与预测

模型输出的预测值进行比较，建立如下优化问题求解感染率α和移除率β：

 min.J=Snx-Sn2+Iνκ-Ip2+R-Rp2,                 (4.5)

 8.l.0.01003≤α≤0.00101,                                 (4.6)

0.0533≤β≤0.1496,                                     (4.7)

其中    Sᵣₛ,lᵣ、Rᵣₛ分别表示实际易感染人数、实际感染人数以及实际移除人数：               Sₚ,lₚ,Rₚ分别表示预测易感染人数、预测感染人数以及预测移除人数。0.0003, 0.0004, 0.0533, 0.1496是对式 (4.4)进行线性回归拟合，得到的未知参数α和β的范围。将3月10日至4月1日的实际数据输入至式(4.5), 并运用 Matlab中的 finincom函数进行求解,得到未知参数α和β的最优解为:                    α=0.00113,β=0.1014。基于发放蔬菜包之前(3月4日至3月25日)的新增感染人数数据，利用MATLAB求解该模型，对无蔬菜包发放情况下的新增感染者人数进行逐日预测，并将预测结果与现实数据进行对比，如下图所示：

SIR 模型预测未发放蔬菜包情况下新增感染者人数峰值为4686人，而发放蔬菜包的现实数据中感染者人数峰值为3823人，且其模型预测峰值出现时间比现实数据晚6天左右。说明发放蔬菜包等防疫措施对疫情的发展起到了一定的抑制作用，有助于提前扑灭疫情。

问题二分为两个小问。第一问考虑物资投放点，需要根据附件2、附件3以及附件4中的数据来讨论投放点数量的合理性并给出合理的投放点的数量分布。第二问考虑物资分拣场所，需要根据附件2、附件3以及附件4中的数据分析得出物资分拣场所的位置分布以及数量规模的选址策略，同时还要给出备用物资分拣场所的选址策略。

在数据处理部分，对位置相同的小区的数据进行合并，随后建立了一个包含所有道路节点以及连接关系的城市交通数据无向图用于辅助建模以及计算距离，同时依照长春市疫情期间的物资发放流程，建立小区节点与路口节点的对应关系，辅助后续最优路径的选取。

在第一小问中，我们分析了附件数据以及2021年长春市统计年鉴中的数据中的隔离人口数(万人)、生活物资投放点数量(个)、小区数量(个)、总感染人数(人)、每万人感染人数、日均蔬菜包接收以及自采数量、日均蔬菜包接收以及自采总重量日均蔬菜包发放数量(袋)、日均蔬菜包发放重量(吨)、区域面积(平方千米)等数据，发现当前的投放点数量分布不合理，容易发放时间慢、拥堵严重能状况。因此，在查阅相关文献的指标以及政府文件后，根据单位面积投放站数量、单个生活物资投放点服务人口数量、单个生活物资投放站日均发放蔬菜包重量以及单个生活物资投放站服务小区数量等指标建立了优化模型。该问题是一个整数规划模型，我们使用 Python+SCIP 求解器进行求解，得到了优化后的投放站数量分布。

在第二小问中，我们使用了弗洛伊德算法计算了各个小区到各个路口之间的距离，建立了一个用于描述距离的矩阵。同时根据相关文献将物资分拣场所设置在路口，简化了分拣场所的位置选择。随后我们在考虑人口分布的基础上建立了以最小化分拣场所到小区之间的距离、最小化分拣场所数量的多目标优化问题并使用遗传算法进行求解根据距离矩阵建立了基于最短距离以及的优化问题。针对该优化问题，我们使用遗传算法进行求解，得到了物资分拣场所的初步位置以及服务的小区范围。最后根据小区和道路的分布位置，适当调整分拣场位置，得到最终的分拣场选址。针对备用场所选址问题，我们在原有模型的基础上，提高分检场数量约束项的权重，即希望分检场的数量较少，得到了备用分检场选址。

5.2 数据处理

5.2.1 重复数据处理

首先，对小区重复数据进行处理。分析附件3“各区主要小区数据”，部分小区横、纵坐标重复，如表5.1所示。对比长春市地图发现，这些小区为同一个小区或同一个小区的南北片区。如表5.2所示，我们对这些横纵坐标一致的小区数据进行合并相加，对于同一地理位置的小区，仅保留其中一个。合并前小区数量有1409个，合并后为1357个。

表5.1    小区重复数据处理前

小区编号     小区栋数     小区户数    小区人口数      小区横坐标    小区纵坐标 所属区域

1139       19         1311       2681       83.84275        17.495      净月区

1202       19       404          964         83.84275       17.495       净月区

960         14         1533       3375         78.4925       45.11033     经开区

970          7         852         1876        78.4925       45.11033     经开区

950          8       1106       2455        74.57675      39.90533     经开区

12

964          6         674         1372       74.57675      39.90533     经开区

247        22       1296       3384        73.27525        57.13        二道区

310         10         1362       3557        73.27525        57.13        二道区

277          2         282          706         69.81875      38.92933     二道区

328          3         188         426         69.81875      38.92933      二道区

表5.2   小区重复数据处理后

小区编号	小区栋数	小区户数	小区人口数	小区横坐标	小区纵坐标	所属区域
1139	38	1715	3645	83.84275	17.495	净月区
960	21	2385	5251	78.4925	45.11033	经开区
950	14	1780	3827	74.57675	39.90533	经开区
964 247	32 5	2658 470	6941 1132	73.27525 69.81875	57.13 38.92933	经开区 二道区

5.2.2 建立交通网络

根据附件3中的交通节点的位置信息、交通节点之间的距离信息、小区位置信息，使用 Python的 networkx 工具建立了如图5.1所示的一个交通网络分布以及小区分布的网络。

依照长春市疫情期间的物资发放的流程，物资发放采取由供应平台集中送货至配送点，再由小区物业、居委会及志愿者组成的配送队伍送货入楼入户的配送模式，保障了疫情期间居民必需品(如蔬菜包)供应。根据配送流程，运输车均不会进入小区，因此我们假定物资运输车停在小区最近的路口，并由小区相关工作人员或志愿者从运输车处搬运蔬菜包送入小区。综上，我们对小区节点和路口节点之间的关系进行处理，连接小区节点以及与小区节点相邻的路口节点，并设置这段距离长度为1，如图5.2所示。小区775与最近的路口7469进行连接，小区821与最近的6840进行连接。

5.3投放站数量分析以及优化

5.3.1 投放站数量分析

首先，我们收集并分析了附件数据以及2020年长春市统计年鉴中的数据，分析结果以及部分数据如表5.3所示。分析发现，二道区和汽开区的投放点密度较低，分别只有0.0093个每平方千米以及0.0833个每平方千米，服务范围分别是107平方千米和12平方千米，这与长春市做疫情防控物资发放中的打通最后一公里的愿景相背。同时我们发现，二道区和汽开区每投放点平均每日服务人数以及每投放点蔬菜日均发放量也存在问题，服务人数过多，投放点蔬菜发放量过高。一方面这会增加投放点压力，降低投放效率，影响居民的日常饮食； 另一方面，同一投放点服务小区数量过多也容易引发人员的频繁接触，增加感染的风险。此外，根据上海等城市的物资投放点的分布情况以及发放情况，长春市可以发挥商超资源优势，通过协调这些资源来保障民生需求。综上，我们认为目前的投放点的数量分布是不合理的，需要进行调整。

表5.3  分析后投放点合理性相关指标

区域名称                朝阳区     南关区      宽城区     绿园区      二道区

隔离人口数 (万人)                    57.8       48.9       32.6       38.5       42.6

生活物资投放点数量(个)                94        261       181     470        9

小区数量 (个)                    200      169      114        146      168

日均蔬菜包接收及自采数量(个/天)                    11982      6701      16273     18236       8659

日均蔬菜包接收及自采重量(吨/天)                   118.14     63.18       133.60      129.54     84.25

区域面积(平方千米)                    237        497      167       301      965

每投放点服务人数(万人/个/日) 每投放点蔬菜日均发放量 (千克/个/日) 投放点密度 (个/平方千米) 每投放点服务小区数量	0.6149    0.1876 1256     242 0.3966    0.5252 2.1277    0.6475	0.1801 738 1.0841 0.6298	0.0819 276 1.5615 0.3106	4.7333 9361 0.0093 18.6667
区域名称	长春新区(高新)	经开区	净月区	汽开区
隔离人口数 (万人)	36.8	20.3	22.8	21.7
生活物资投放点数量 (个)	215	37	279	10
小区数量 (个)	184	202	141	85
日均蔬菜发放数量 (个/天)	8832	9420	5820	4344
日均蔬菜发放重量 (吨/天)	80.27	118.80	57.22	56.15
区域面积 (平方千米)	499	112	478	120
每投放点服务人数(万人/个/日)	0.1712	0.5486	0.0817	2.1700
每投放点蔬菜日均发放量 (千克/个/日)	373	3210	205	5614
投放点密度 (个/平方千米) 每投放点服务小区数量	0.4309 0.8558	0.3304 5.4595	0.5839 0.5054	0.0833 8.5

5.3.2 投放站数量优化

基于民生物资的保障角度，投放站建立的目的就是为了保证居民的物资需求，因此投放站分布应当考虑单位面积投放站数量、单个生活物资投放点服务人口数量、单个生活物资投放站日均发放蔬菜包重量以及单个生活物资投放站服务小区数量等指标。但投放站的数量并不是越多越好，要考虑投放站的运营成本以及是否会增加感染风险。过多的投放站势必会造成人力资源的浪费以及交叉感染的风险的提升。综合考虑上述因素，我们建立了各区的投放点数量优化模型。

对于优化问题的目标函数，我们要考虑居民的物资需求的保障，因此希望每个投放点服务人数(万人/个) 尽可能少、每个投放点发放蔬菜包数量(个/个) 尽可能少、每个投放点服务的小区数量(个/个) 尽可能少。设定目标函数为

 min∑t∈VWP+CxMk2xn                          (5.1)

其中W是一个1×3 维的一个系数矩阵，起到了消除各个参数之间数量级不同以及设置权重的功能。优化问题的约束条件为

 xλ0.318A,i∈V                              (5.2)

 ∑k∈Vxi≤∑i∈VPrϵi,1.2                            (5.3)

 x3∈N*,i∈V                               (5.4)

本问题中，x：为优化变量，代表了优化后第i个区的投放点的数量。约束5.2是基于长春市长春市做疫情防控物资发放中的打通最后一公里的愿景，设置平均一个投放站数量服务的面积应不大于3.14平方公里，即每平方公里至少要有0.318个投放站。约束5.3是投放站数量的约束，出于人力成本考虑，优化后的投放站数量应不超过优化前的1.2倍。

代码

 clo; clear

 load 'questionlSIR. mat'

[t,x]=ode45('SIR  differential   equation',[1:500], [N-10 i0 0]);

x = round(x);

 figure(1)

 plot(t,x(:,2),"b-',' Linewidth',1.5)

 legend('患者I')

SIR  differential   equation. m

 function dx=SIR  differential   equation{t,x}

 beta= 0.0013; % 感染率

 gamma = 0.1014; % 移出率

 dx = zeros(3,1); % x(1)表示3 x(2)表示I x(3)表示R

C = x(1)+x(2); % 传染病系统中的有效人群

 dx(1) = - beta*x(1)*x(2)/C;

 dx(2} = beta*x(1)*x(2)/c- gamma*x(2);

 dx(3) = gamma*x(2);

 end

B.2     问题2代码

 myflowd. m

 function [ dist, mypath]= myflowd(a, sb, db);

n= size(a,1); path= zeros(n);

 for k=1:n

 for i=1:n

 for j=1:n

 if a(i,j)>a{i,k}+a(k,j}

a(i,j)=a(i,k)+a(k,j);

 path(i,j}=k;

 end

 end

 end

 end

 dist=a( sb, db);

 parent= path( sb,:);

 parent( parent==0)= sb;

 mypath= db;t= db;

 while t-= sb

p= parent(t); mypath=[p, mypath];

t=p;

 and

 end

$A. m

 function [ dist,= ypath]= myflowd(a, sb, db);

n= size(a,1); path= zeros(n);

 for k=1:n

 for i=1:n

 for j=1:n

 if a(i,j)>a(i,k)+a(k,j)

a(i,j)=a(i,k)+a(k,j);

 path(i,j}=k;

 end

 and

 end

 end

 dist=a( sb, db);

 parent= path( sb,:);

 parent( parent==0)= sb;

 mypath= db;t= db;

 while t-= sb

p= parent(t); mypath=[p, mypath];

t=p;

 end

 end

B.3     问题3代码

DEA. m

 clear

 clo

 format long

 load ' question 3DEA. mat'

X=DEAdata([1:3],:); %投入指标数据

Y=DEAdata(4,:}; 行出指标数据

Y = { max(Y) - Y)/ max(Y)- min(Y): 对产出数据进行正向化

[m,n]= size(X); %输入变量个数与样本数

s= size(Y,1); %输出变量个数

A=[X' Y'];

b= zeros(n,1);

LB= zeros(m+s,1);UB=[];

 for i=1;n

f=[ zeros(1,m) -Y(:,i)'];

 Aeq=[X(:,i)', zeros(1,s)];

 beq=1;

w(:,i)= linprog(f,A,b, Aeq, beq,LB,UB) ;

E(i,i)=Y(;,i)'*ω(m+1;m+s,i};

 for j=1:100

w(:,i)= linprog(f,λ,b, Aeq, beq,LB,UB, randn(11,1));

D(i,i)=Y(:,i)'*w(m+1;m+s,i);*产出值乘产出系数

 if D(i,i)<E(i,i)

E(i,i}=D(i,i)

 end

 end

 end

 theta= diag(E)';

fprintf('使用数据包络分析方法对各决策单元的相对评价结果为：\n')；

 disp( theta);

B.4     问题4代码

DEA. m

# data from excel

 supply   capacity = []

 demand = []

 fix   cost  1st = []

 location = np. random. randint(0,2,5)

 import pandas as pd

 import numpy as np

 import pulp

 import math

 import matplotlib. pyplot as plt

 data = pd. read   csv(r' transcost. csv'}

demand = [729, 630, 321, 293, 251, 573, 207, 732, 481, 783]

 supply   capacity = [4500, 3500, 5000, 3000, 2500]

 fix   cost   lst = [304, 281, 459, 292, 241]

 dic = {0:'A',1:'B',2:'C',3:'D',4:'E'}

 def Cal   total   capacity( location, capacity):

 total   capacity  1st = [ capacity[i] for i in range( len{ location}) if location [i] == 1]

 return sum( total   capacity   lst)

 def fixpop( location, capacity, demand):

 while sum( demand) > Cal   total   capacity( location, capacity):

 ind = np. random. randint(0, len( location))

 if location[ ind] == 0:

 location[ ind] = 1

 return location

 def Get   Translist( location, data, dic):

 transcost = [ list( data[ dic[i]]) for i in range( len( location)) if location[i ] == 1]

 return transcost

 def transportation   problem( costs, x  max, y  max):

 row = len( costs)

49

 col = len( costs[0]}

 prob = pulp. LpProblen(' Transportation Problem', sense= pulp. LpMinimize)

 var = [[ pulp. IpVariable(f'x{i}(j}', lowBound=0, cat= pulp. LpInteger} for j  in range( col)] for i in range( row)]

 flatten = lambda x: (y for l in x for y in flatten(l)] if type(x) is list  else [x]

 prob += pulp. lpDot( flatten( var), costs. flatten())

 for i in range( row):

 prob += ( pulp. lpSum( var[i]) <= x  max[i])

 for j in range( col}:

 prob += { pulp. lpSum([ var[i][j] for i in range( row}]) == y  max[j])

 prob. solve()

 return {' objective': pulp. value( prob. objective), ' var': [[ pulp. value( var[i][j]) for j in range( col)] for i in range( row)]}

 def Cal   cost( location):

 pop = fixpop( location, supply   capacity, demand)

 fix   cost = 0

 capacity   new = []

 for i in range( len( pop)}:

 if pop[i] == 1:

 fix   cost += fix   cost   lst[i]

 capacity   new. append( supply   capacity[i])

 translist = Get   Translist( pop, data, dic)

 max   plant = capacity   new

 max   cultivation = demand

 res = transportation   problem( costs, max   plant, max   cultivation)

 return res[' var'], res[" objective"] + fix   cost

 def GetInitialTem( location):

cost1 = 0 ; cost2 = 0 ; dif = 0

 for i in range(10):

 location l = list( np. random. permutation( location))

 location 2 = list( np. random. permutation( location))

cost1 = Cal   cost( locationl)[1]

cost2 = Cal   cost(location2)[1]

difNew = abs(cost1 - cost2)

 if difNew > dif:

 dif = difNew

 pr = 0.5

TO = dif / pr

 return TO

 def Disturbance( location   old):

 location   new = location   old. copy()

 ind = np. random. randint(0, len( location   new))

 if location   new[ ind] == 0:

 location   new[ ind] = 1

 else:

 location   new[ ind] = 0

 return location   new

 def Judge(deltaE,T):

 if deltaE < 0:

 return 1

 else:

 probility = math. exp(-deltaE/T)

 if probility > np. random. random():

 return 1

 else:

 return 0

 location = np. random. randint(0,2,5)

ValueOld = Cal   cost( location) [1]

 count = 0

 record   value = []

 tmp = GetInitialTem( location)

 tmp   min = 1e-5

 alpha = 0.98

 while ( tmp > tmp   min and count < 2000):

 location  n = Disturbance( location)

 location   new = fixpop( location  n, supply   capacity, demand)

ValueNew = Cal   cost( location   new) [1]

deltaE = ValueNew - Value0ld

 if Judge(deltaE, tmp) == 1:

 location = location   new

# print(ValueNew)

Value0ld = ValueNew

 record   value. append(ValueNew)

 if deltaE < 0 :

 tmp = tmp * alpha

 else:

 count += 1

 print('='*80,'\n',

' The minvalue is: ()'. format( min( record   value)),'\n',

' The best location is: (I'. format( location),'\n',

' The best transport schedule is: ()'. format( Cal   cost( location)[0]),'\n',

'='*80}

x = len( record   value)

 index = [i+1 for i in range(x)]

 plt. plot( index, record   value)

 plt. xlabel(' iterations')

 plt. ylabel(' minvalue')

 plt. title(' Simulated Annealing')