2023年华为杯数学建模竞赛题D论文和代码

双碳目标下基于 kaya-LMDI模型的区域碳排放预测及路径设计

步入新发展阶段，能否平衡区域经济增长与“双碳”目标实现是关乎一地区经济能否高质量发展的关键所在。面对日益严峻的碳排问题，亟需探究区域能源消费碳排放的驱动因素，寻求其与经济增长之间的脱钩趋势。本文以能源利用效率和非化石能源消费比重为切入点，依照“现状分析-趋势预测-路径规划”框架，利用数据挖掘、数据分析、统计建模等方法，积极探索双碳背景下破解发展与减排矛盾的合理路径。

针对问题一：首先，结合附件数据，基于传统 kaya模型构建指标体系，分部门对经济发展、人口规模、能源消费量和碳排放量进行描述：其次，通过绘制该区域十二五、十三五期间碳排放总量与上述指标的时序图，可视化分析2011-2020年碳排放量现状，并从4个方面分析该区域实现双碳目标的主要挑战，为该区域双碳路径设计中的路径选择提供依据：最后，在 kaya模型的基础上构建 kaya-LMDI模型，分析对该区域碳排放量产生影响的各因素，同时探究相关指标变动带来的影响，结合双碳政策与技术进步等多重效应，最终确定碳排放预测模型参数。

针对问题二：首先对中国式现代化两个节点的奋斗目标进行分析，以2020年为基期，结合收获函数, 选取改进的 Logistic 增长模型和ARIMA 模型分别对2021-2060年该区域人口和GDP进行预测，同时借助线性多元回归方程预测能源消费量的变化趋势； 然后在问题一建立的指标体系基础上，新增能源能效这一指标。并利用能源能效、能源消耗强度、能源结构强度、经济发展和人口规模这五大因素构建预测区域碳排放量的STIRPAT 模型，最终得到满足条件要求的区域碳排放预测模型。

针对问题三：首先，设计基准情景(BAU)、低碳情景(S1) 、达峰情景(S2) 、强化达峰情景 (S3)、中和情景(S4) 以及强化中和情景(S5)6类碳中和碳达峰的路径情景。其次，运用LEAP模型对各情景、各部门逐年能源消费、碳排放量及碳排放达峰时间进行预测分析。同时基于问题二所建立的预测模型，对区域碳排放量进行双碳目标和中国现代化两个要求的约束，从而得到指标预测值。最后，对该区域实现双碳目标进行路径设计及定量与定性分析。

关键词:双碳目标 kaya-LDMI模型 STIRPAT 模型 LEAP 模型 路径研究

1 问题综述

1.1 问题背景

据2021年国际能源署(IEA)数据显示，中国二氧化碳总排放量达到119亿吨以上，占全球碳排放总量的33%，已经成为世界碳排量第一大国。作为世界上最大的二氧化碳排放国，中国政府在第七十五届联合国大会一般性辩论上郑重提出2030年“碳达峰”与2060年“碳中和”的“双碳”目标。随后，国家出台了一系列政策进行战略部署与执行，如《关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见》《2030年前碳达峰行动方案的通知》《工业领域碳达峰实施方案》等。2022年，党的二十大报告再次强调要积极稳妥地推进“双碳”目标的达成，并从碳排放双控、能源革命、健全碳市场、提升碳汇能力等方面进行了具体部署。

当前，我国经济发展正处于由高速增长向高质量发展的转型关键期，党的二十大报告提出，全面建成社会主义现代化强国，总的战略安排是分两步走：从二○二○年到二○三五年基本实现社会主义现代化； 从二○三五年到本世纪中叶把我国建成富强民主文明和谐

1 数据来源: Our World in Data

关注数模加油站，助力竞赛赢满贯

美丽的社会主义现代化强国。因此，我们迫切需要统筹“双碳目标”与“中国式现代化目标”，破解碳减排与经济发展之间的矛盾，在积极推动双碳目标达成的同时实现我国经济的高质量发展。

能源消费是碳排放的重要来源。分析区域能源消费碳排放的驱动因素探究其与经济增长之间的脱钩趋势是当前亟待解决的重要问题。为了寻求经济增长与碳排放量的负相关变化，本赛题聚焦提高能源利用效率和提高非化石能源消费比重两个方面。一方面，通过提高能源利用效率，实现经济增长与能源消费量增长的负相关变化； 另一方面，通过提高非化石能源消费比重，实现能源消费量与碳排放量增长的负相关变化。进一步地，可以通过实施能效提升和产品/产业升级两种手段提高能源利用效率(即降低单位GDP能耗) ，通过能源脱碳和能源消费电气化实现非化石能源消费比重的提升(即降低单位能耗碳排放)。

符号说明

符号	说明
GHG	区域碳排放量
TOE	能源消耗总量
GDP	国内生产总值
POP	人口总数
GHG TOE	碳排放强度
TOE GDP	能源消耗强度
GDP POP	人均国内生产总值
C	区域碳排放总量
C₁	第i个部门产生的碳排放量
EC₁	第i个部门化石燃料消耗量
E₁	第i个部门能源消耗量
CEC₁	第i个部门化石燃料碳排放强度
EC₁E₁	第i个部门能源结构强度
E,D	第i个部门能源消耗强度
C. C.	人均GDP
CO	基期碳排放量
CT	T期碳排放量
ΔC	基期至周期T区域碳排放变化总量
△CC	表示第i个部门化石燃料碳排放强度效应

△CEC	表示第i个部门能源结构效应
△CE	表示第i个部门能源强度效应
△Ccare	表示第i个部门经济产出效应
△C,	表示人口规模效应
S	能源结构
N	能源消耗
E	经济发展
P	人口规模
e	能源结构强度
k	能源消耗强度
λ₁	部门i在区域碳排放量中所占比重
r	表示人口增长率 (即出生率减去死亡率)
c	环境承载力
EE	能源能效
EC	能源消耗强度
ES	能源结构强度
E	经济发展
P	人口规模
BAU	基准情景
S1	强化低碳情景
S2	达峰情景
S3	强化达峰情景
S4	中和情景
S5	强化中和情景

(1) 某区域碳排放总量与宏观经济总量

某区域的宏观经济水平在“十二五”期间和“十三五”期间，GDP 总量趋于稳步的增长；碳排放量在“十二五”期间存在缓步下降的阶段，在进入“十三五”期间表现为缓步增长：某区域的人口总量在“十二五”到“十三五”期间一直保持持续的增长，但增速逐渐变慢； 某区域的能源消费量和化石燃料消耗总量总体趋于一致，在进入“十二五”期间有一个较大的增长，在“十二五”期间总体趋于平稳，在“十三五”期间处于一个缓步增长的阶段，并在“十三五”的最后一年明显降低了增速，并出现缓步降低的趋势。由于探究的各变量单位都有所不同，所以进行了取对数的处理，消除单位对各变量变化程度的影响，具体绘制如时间序列图如图3-1所示。

(2) 某区域不同产业部门的碳排放量状况

关注数模加油站，助力竞赛赢满贯

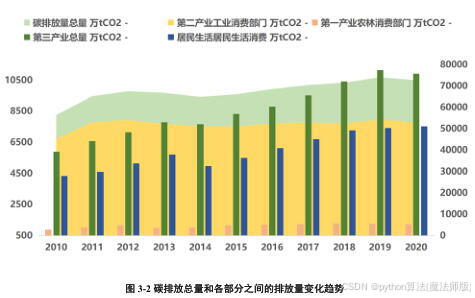
①碳排放总量。某区域的经济结构以第二产业为主，尤其是重化工业占据主导地位，是典型的工业主导型经济。该区域的三次产业及居民生活的碳排放量中，第二产业的碳排放量比重最大, 超过70%, 2012 年达到峰值, 碳排放量为54048.28t, 占比80.06%, 但从之后开始下降。第三产业比重相对比较平稳，维持在11%左右。能源消费总量处于持续上升态势，但增速自“十二五”开始持续降低。该区域的碳排放总量在“十二五”期间存在缓步下降，增长速度进入“十三五”期间表现为在波动中逐渐趋缓。碳排放总量和各部分之间的排放量变化趋势如图3-2所示。

碳排放总量和各部分之间的排放量变化趋势

②碳排放总量的增长率。该区域的碳排放总量从增速来看，2011年高达15.6%，2012年增速降至3.54%, 2013、2014年继续回落, 2015、2016年有小幅回升, 2018年增速达到4.05%。碳排放总量与各部门碳排放量增长率如图3-3所示。

 

3.2.2对某区域碳排放量产生影响的各因素及其贡献

通过3.1我们根据对区域碳排放量产生主要影响的因素建立了四种指标，分别是能源结构、能源消耗、经济发展和人口规模，本小节将基于这四种指标探究四种因素对区域碳排放量的影响贡献度。

(1) 碳排放量影响因素模型

由于本小节不计算碳排放量的综合，仅考虑碳排放量的影响因素，因此不考虑不同部门的总和，简化3.1中的公式为

 CP×ECE×EGDP×6DPP

= Pxexkxi                            (3.5)

式中, C——碳排放量(万 t) :

P———人口总数；

e——能源结构强度：

k——能源消耗强度：

i———人均GDP。

某区域碳排放在2010—2020年这段时间内(设[0,T]) , 碳排放变化从C⁰到 CT用加法模式进行分解后得3.6公式：

 ΔC=Cʳ-C⁰

 =PI×eI×kI×iT-P0×e0×k0×i0           (3.6)

=ΔP+Δe+Δk+Δi

公式等号左边为某区域碳排放的变化量，右侧表示各种驱动因素的影响。根据指数分解的定义，取目标变量对时间T的导数，得各分解因素贡献值表达式如3.7、3.8、3.9、3.10所示：

 Dcp=∑c7-c0lnCr-imC0×lnxppxpn                          (3.7)

 Dcc=∑cT-c∘lnc1-lnc0×lnXrtXo∞                            (3.8)

 Dck=∑c1-c∘lnc1-mc0×lnXitxμv                            (3.9)

 Dc1=∑c1-c0lnc1-lnC0×lnXirXi9                           (3.10)

计算所需数据选取2010-2020年某区域统计年，汇总结果如表3-2所示：

表3-2 2010——2020 年某区域碳排放驱动因素值

年份	人口规模(万人)	能源结构强度	能源消耗强度	人均GDP (万元/人)
2010	7869.340	0.964	0.569	5.258874315
2011	8022.990	0.968	0.585	5.727621498
2012	8119.810	0.963	0.553	6.239086875
2013	8192.440	0.956	0.507	6.784317004
2014	8281.090	0.947	0.467	7.288826712
2015	8315.110	0.948	0.443	7.883479593
2016	8381.470	0.946	0.424	8.431182934
2017	8423.500	0.937	0.405	8.992960348
2018	8446.190	0.925	0.388	9.569724566
2019	8469.090	0.919	0.377	10.10216374
2020	8477.260	0.913	0.354	10.46130644

(2) 碳排放影响因素结果分析

如图3-5 所示, 2010—2020年间, 某区域碳排放量增长16273.27万吨。从分解结果看，人口规模、能源消耗强度、能源消费结构三种驱动因素对碳排放呈现负效应，分别为-6.58%、-213.21%、-41.84%,其中能源消耗强度从0.569下降到0.357, 减碳效果显著。人均GDP对某区域碳排放呈现促进作用，贡献度为361.63%，某区域生产总值从2011年41383.87亿元增长到2020年88683.21 亿元,由此可见经济增长是某区域碳排放增加的主要驱动因素。

2010-2020年碳排放量影响因素的效应结果 ■人口规模■能源消耗强度1能源结构强度■人均GDP
			361.63%
6.58%	-213.21%	-41.84%
人口规模        能源消耗强度       能源结构强度			人均GDP

图3-52010-2020年碳排放量影响因素的效应结果

3.2.3某区域实现碳达峰与碳中和需要面对的主要挑战

(1) 碳排放总量基数大，减排挑战压力大

2030年实现碳达峰，2060年前实现碳中和，意味着我们要用不到十年时间扭转温室气体排放持续增长的局面，用三十年实现零碳排放，这对于工业化和城镇化迅速发展的中国来说充满挑战。西方国家工业化发展起步早、时间长、水平高，碳达峰到碳中和大多需要50—60年，如英国59年、法国59年、德国超过60年、瑞典52年，我国从碳达峰到碳中和时间仅为西方国家的一半，时间非常紧迫。

我国是世界上温室气体排放量最大的国家，  《中国2060年前碳中和研究报告》指出2014年我国温室气体排放总量相较2005年增长54%，2019、2020年碳排放量占全球碳排放量的27%、30%,2019年我国碳排放量是美国的近2.5倍, 2020年是美国的2.2倍。西方国家低碳转型建立在高水平工业发展基础上，部分国家直接通过自然达峰的形式实现碳达峰，而我国既要保证经济稳定发展，又要顺利实现“双碳”目标，时间短，任务艰巨，难度史无前例。

普通最小二乘法估计结果

部门	项目	非标准化系数		标准化系数	显著性检验		共线性检验
		系数	标准误差	标准系数	t	s1g	VIF
	常数	7.844	7.935	—	0.989	0.368	—
	LNEE	-0.201	0.074	-0.097	-2.725	0.042	1.764
农林消费部门	LNEC	1.111	0.076	0.997	14.574	0.000	6.56
	LNES	-1.043	0.205	-0.472	-5.1	0.004	11.971
	LNE	1.143	0.147	1.185	7.782	0.001	32.485
	LNP	0.184	0.868	0.037	0.212	0.841	43.906
	常数	-21.429	50.320		-0.436	0.688
	LNEE	2.075	1.689	1.331	1.228	0.274	40.863
能源供应部门	LNEC	0.558	2.546	1.098	0.219	0.835	874.521
	LNES	-0.163	0.353	-0.310	-0.461	0.664	15.683
	LNE	0.739	1.913	1.726	0.386	0.715	694.139
	LNP	3.578	5.666	0.877	0.631	0.555	66.985
	常数	20.620	13.661		1.509	0.192
	LNEE	-0.757	0.159	-1.146	-4.749	0.005	3.909
工业消费部门	LNEC	2.037	0.821	4.092	2.481	0.056	182.377
	LNES	1.147	1.112	0.672	1.031	0.350	28.441
	LNE	1.684	0.592	5.635	2.845	0.036	262.999
	LNP	-1.179	1.550	-0.583	-0.760	0.482	39.462
	常数	2.825	3.130		0.902	0.408
	LNEE	-0.022	0.037	-0.018	-0.576	0.589	33.756
交通消费部门	LNEC	0.988	0.101	0.418	9.798	0.000	64.154
	LNES	-2.017	0.766	0.068	-2.633	0.046	23.486
	LNE	0.973	0.094	0.535	10.334	0.000	94.456
	LNP	0.756	0.338	0.093	2.239	0.075	60.556
	常数	99.595	22.994		4.288	0.008
	LNEE	-0.705	0.154	-0.514	-4.584	0.006	22.019
建筑消费部门	LNEC	1.515	0.132	1.106	11.484	0.000	16.262
	LNES	0.047	0.035	0.176	1.370	0.229	28.89
	LNE	2.494	0.334	3.706	7.478	0.001	430.59
	LNP	-9.955	2.584	-1.085	-3.852	0.012	139.25
	常数	18.998	5.808		3.271	0.022
	LNEE	-0.315	0.077	-0.321	-4.563	-0.006	11.832
居民生活消费	LNEC	1.406	0.144	0.64	9.735	0.000	10.297
	LNES	-0.840	0.206	-0.124	-4.074	0.010	2.212
	LNE LNP	1.304 -1.045	0.131 0.635	0.866 -0.13	9.976 -1.672	0.000 0.155	17.954 14.501

由表4-8可知，区域碳排放量与各指标因素之间的相关性较高，为判断多重共线程度，首先对各变量采用最小二乘法进行检验，所有变量的方差膨胀因子远远高于最大容忍度10，

41

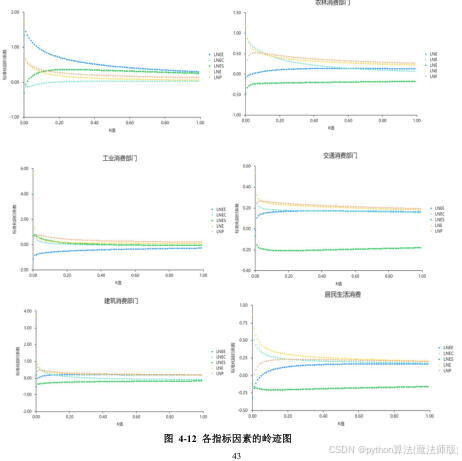
多重共线性程度较高。为避免该现象，基于STIRPAT模型，选用岭回归方法来拟合方程，得到该区域各部门碳排放量与各指标因素的岭迹图，见图4-12。

分析图4-12，不难发现K=0.01各自变量回归系数变化趋于平稳，所以本文取 K=0.01时的岭回归结果确定随机模型，从而拟合方程分别为：

 In C农林消费部门=-10.493-0.057lnEE+0.882lnEC-0.634lnES+0.735lnE+2.187LNP

 In C能源供应部门=-9.755+2.097lnEE-0.072lnEC+0.014lnES+0.234lnE+2.321lnP

 ln C工业消费部门=-2.5-0.522lnEE+0.232lnEC+1.143lnES+0.234lnE+1.493lnP

 In C交通酒费部门=-8.392+0.125lnEE+0.582lnEC-4.680lnES+0.591lnE+1.957lnP

 ln C建筑消费部门=-22.865-0.047lnEE+0.866lnEC-0.094lnES+0.58lnE+3.684lnP

 ln C居民生活消费=8.581-0.206lnEE+1.110lnEC-1.076lnES+1.022lnE+0.078ln P

K=0.01时岭回归分析结果如表4-9所示：

表 4-9 k=0.01时岭回归结果

部门	项目		非标准化系数	显著性检验	R方	F值
		系数	标准误差	t
	常数	-10.493	5.467	-1.919
	LNEE	-0.057	0.112	-0.511
农林消费部门	LNEC	0.882	0.092	9.552	0.989	97.187
	LNES	-0.634	0.214	-2.967
	LNE LNP	0.735	0.11	6.658
		2.187	0.598	3.658
	常数	-9.755	18.502	-0.527
	LNEE	2.097	0.565	3.711
能源供应部门	LNEC	-0.072	0.15	-0.477	0.844	5.404
	LNES	0.014	0.183	0.079
	LNE	0.234	0.152	1.538
	LNP	2.321	2.086	1.112
	常数	-2.5	8.215	-0.304
	LNEE	-0.522	0.15	-3.479
工业消费部门	LNEC LNES	0.232 1.143	0.226 0.835	1.024 1.369	0.829	4.865
	LNE	0.234	0.116	2.023
	LNP	1.493	0.926	1.612
	常数	-8.392	2.631	-3.19
交通消费部门	LNEE LNEC	0.125 0.582	0.033 0.069	3.732 8.467	0.999	1593.87

	LNES LNE LNP	-4.68 0.591 1.957	0.942 0.061 0.288	-4.97 9.711 6.793
	常数	-22.865	14.804	14.804
	LNEE	-0.047	0.28	0.28
建筑消费部门	LNEC LNES	0.866 -0.094	0.245 0.05	0.245 0.05	0.977	43.002
	LNE	0.58	0.14	0.14
	LNP	3.684	1.672	1.672
	常数	8.581	6.274	1.368
	LNEE	-0.206	0.087	-2.373
居民生活消费	LNEC LNES	1.11 -1.076	0.155 0.266	7.163 -4.047	0.996	235.631
	LNE LNP	1.022 0.078	0.133 0.675	7.697 0.116

由表4-9可知，各部门拟合优度R²、拟合模型的 F检验显著，各个因素的回归系数均符合现实意义检验，可知该模型拟合程度高，可进行后续的区域碳排放预测。在由此可得各部门STIRPAT 碳排放预测模型为：

C农林消费部门=e⁻¹⁰.493-0.057hEE+0.8821mEC-0.634lnE3+0.755hE+2.1871=”  (4.15)

C能源供应部门=e⁻⁹.755+2.097hnEE-0.072hnEC+0.0141mES+0.234lnE+2.321h²”    (4.16)