2023年高教社杯全国大学生数学建模竞赛题目C题蔬菜类商品的自动定价与补货决策

基于历史数据的蔬菜类商品定价与补货决策模型

农业是国民经济的重要支柱,农产品市场的稳定是国家经济平稳健康运行的有力支撑。蔬菜类农产品作为农产品一大类别，对其商品定价和补货决策问题的研究具有十分重要的意义。本文针对以上问题，根据蔬菜销售、进价和定价等数据，并基于K-S检验、ARIMA模型和 Prophet 模型等研究方法，对蔬菜销量的分布规律进行了详细分析，建立基于历史数据的蔬菜类商品定价与补货决策的模型，并使用模拟退火算法、遗传算法等对该模型进行了求解。

针对问题一，首先进行数据预处理，针对蔬菜销量流水的缺失值和异常值等进行了相应的处理操作，并对数据分类汇总以获得各单品或品类不同维度的销量数据。之后，首先先从总体的角度去分析不同品类蔬菜的分布规律及相互关系。分别使用 K-S 检验、皮尔逊相关系数矩阵、ARIMA时间序列分析等方法，对销量数据从不同的维度进行整体分析；之后认为再从周、月、年等多个维度，利用可视化分析和相关系数矩阵等方法，详细分析不同品类蔬菜的分布规律及相互关系。

针对问题二，本文首先单品数据合并为品类数据，并编制能够反映品类价格特点的量化指标。使用以销售价格为外生变量的Prophet模型，分离出品类销售总额数据的趋势项、季节项、节假日项，通过调整后的线性回归模型在小区间内建立了成本加成定价与销售总额的关联。最后将Prophet模型结合模拟退火的启发式算法，优化7月1日至7月7日的自动定价策略与补货方案。

针对问题三，首先根据 2023 年 6 月 24-30 日的市场批发价情况筛选出可以 7 月 1日可以从供应商处批发获得的蔬菜单品。之后，结合实际情况和历史数据，预测出当天各单品蔬菜的市场需求量与进货价格。此外，结合问题二的 Prophet 模型，建立出各单品蔬菜销量与其定价之间的线性关系。基于上述分析，构建出混合整数二次规划，并结合遗传算法，获得相应的最优解，提供7月1日的自动定价与补货方案。

针对问题四，结合前三个问题的分析和建模过程，提出获取疫情封控状态等数据以补足完善之前的补货和定价模型；此外，针对前文利用不足的折扣率、损耗率等数据，提出获取库存最大容量、隔天库存损耗率等数据，以更好地利用和分析这些数据，并建立相应的动态规划模型，作为补货和定价模型的补充。

关键词： ARIMA    Prophet模型   模拟退火   遗传算法

一、 问题重述

1.1  问题背景

在生鲜商超中，由于蔬菜类商品保质期较短，商超会每天进行补货。由于蔬菜每日的进货交易时间在凌晨，因此商家并不确切知道具体单品和进货价格，而只能根据各商品的历史销售和需求情况进行每日的补货决策。另外，蔬菜的定价采用“成本加成定价法”，对运损或品相变差的商品通常打折销售处理。

因此，需要对市场需求和供给进行合理分析，从而进行补货和定价决策。从需求侧看，蔬菜类商品的需求在时间上存在周期性，其销售量与时间存在一定的关联性；从供给侧来看，蔬菜的供应品种在 4 月到 10 月较为丰富，商超销售空间的限制使得合理的销售组合变得极为重要；结合需求侧和供给侧，可以分析各蔬菜品类的销售总量与成本定价之间的关系，从而进行合理的优化决策。

1.2  问题提出

          问题是层层递进，并且服务于同一主题的——如何通过分析蔬菜的已有成本、定价和销量等历史数据，从而制定出合理的补货和定价决策，实现商超利润最大化： 问题一：根据附件1和附件2，按照周、月、年等不同的分析维度，分析蔬菜各品类及单品销售量的分布关系，以及其相互关系；
          问题二：在对各蔬菜品类与单品销量分析的基础上，进一步分析决定各蔬菜品类市场需求的可能因素，从而确定不同的成本加成定价水平对市场需求的影响，并给出各蔬菜品类2023年7月1-7日的日补货总量和定价策略，使商超利益最大化；
          问题三：在可售单品总数控制在 27-33 个，且各单品订购量满足最小陈列量 2.5 千克的前提下，尽量满足市场对各品类蔬菜商品的需求，同时根据 2023 年 6 月 24-30 日的可售单品，给出7月1日的单品补货量和定价策略。

          问题四：结合以上问题的分析和建模过程，希望商家继续采集哪些相关数据，从而可以完善模型并更好地制定蔬菜商品的定价和补货决策。

二、 问题分析

问题一：研究对象为蔬菜各单品和品类的销售量，而附件2仅提供了三年内各单品蔬菜的销售流水数据，因此要先对该数据进行预处理。首先需要观察分析原始数据，检查是否有缺失值、异常值等，并进行相应的处理。其次，需要将附件1和附件2的表格进行匹配，对数据进行加总，分别获得各单品和各品类蔬菜的日销售量、周销售量等数据。之后，才能对蔬菜各单品、品类的销售分布和相互关系进行分析。

针对不同品类蔬菜的总体分布规律及相互关系，可以首先从总体的角度把握数据，如进行假设检验、模拟拟合和可视化分析等操作；之后再从周销量、月销量和年销量的角度分别详细分析其分布规律及相关系数。

问题二：在探讨成本加成定价水平与市场需求的关联时，需要先剔除由季节性、趋势性、特定时间段带来的影响。从供给端看，蔬菜市场受季节、年景等因素影响较大，不同季节上市的蔬菜单品组合亦有显著差异；从需求端看，消费者在周末、特定节假日期间会加大对蔬菜的购买力度；同时由于可供选择的蔬菜品类较多，市场需求存在显著的替代效应，因此需要编制合适的量化指标来概括品类的价格表现。由于消费者的行为直接取决于蔬菜的绝对价格，间接受到成本利润率的影响，需要先关注蔬菜销售价格与市场需求的关联，再由销售价格和批发价格反推出成本加成定价的加成比率。解决该问题首先要建立合适的预测模型，预测各蔬菜品类在2023年7月1日至2023年7月7日的市场需求，再使用优化模型建立合理的补货策略和自动定价策略（即成本加成比率）以最大化商超收益。

问题三：本问题是一个混合线性优化问题需要结合问题二中分析出的销售价格与进货量的关系，作为变量间的条件。同时，题目中要求的尽量满足品类的需求也需要结合实际的利润情况、季节性、噪点等情况，截取合适时间段内的销售记录进行分析，之后，进一步结合题目要求确定约束条件。由于变量数较多，使用启发式算法中的遗传算法进行求解。求解后需要进一步分析约束的实际满足情况，以确定是否能够在满足品类需求的同时，控制进货量保证能够符合模型假设。

问题四：应当结合前三个问题的分析和建模过程。结合问题一对销量分布规律和相互关系的分析，可以联想找出影响销量的潜在因素，从而更好地分析销量的规律；结合问题二和问题三，可以寻找出定价和补货模型中缺少的数据和信息。此外，可以从之前模型中利用不足的数据切入，例如折扣率、退货率等，思考利用可以如何分析利用这些数据，并据此补足缺乏的数据，从而更好地构造模型。

三、 模型假设与符号说明

3.1  模型基本假设

 商超的客群基本稳定，消费者行为在短期内可以预测；

 可供选择的蔬菜单品已经全部给出，不考虑新增的蔬菜单品；

 市场环境在预测期内不会发生巨大改变，经营可以保持连续稳定。

3.2  符号说明

表1 符号说明

符号

含义

市场对品类i的需求

 

Prophet模型的趋势项 Prophet模型的周期项 Prophet模型的节假日项 价格对需求的影响函数 Prophet模型的残差 单品j的销售价格 单品j的销量 单品j的批发价格 品类i的销售价格指数 品类i的总销量 品类i的批发价格指数 品类i的平均损耗率 品类i的平均折扣率

四、 问题一模型建立与求解

4.1  问题一求解思路

首先，通过代码观察分析四个附件，发现没有直观意义上的缺失值。但是，对于单个单品而言，必定有一些日期没有销售记录，甚至由于蔬菜的季节特殊性，许多单品会出现很长时间的没有销售记录。

因此，针对三年来总销量很少的单品，在计算单品间相关系数的环节，删去了总销量后25%的单品，一方面因为缺失值过多的单品之间往往无法找到相同的时间点进行销量对比，另一方面缺失值过多也会对于相关系数的计算产生偏高或者偏低的影响。而对于留下的单品，没有销售记录的日期用0来填充销量。

另外，对于分布规律的比较，由于不同的品类及不同的单品之间存在着较大的销量绝对值差异，因此按照一定时间范围内的销量比例来计算，比如计算月销量规律时，将每个品类或单品的每个月销量除以总销量，以得到月销量比例其他时间维度同理，方便不同品类或单品之间的比较。

此外，由于日常中偶然性因素，比如疫情封控、极端天气等情况，各单品蔬菜的日销量会出现部分异常的极端值。这些极端值可能会对后续分析造成不良影响，因此，借鉴箱线图的定义，记各单品蔬菜的上四分位点、中位数、下四分位点为 Q3、Q2 和 Q1，记四分位距IQR=Q3-Q1。获取各单品蔬菜中超出正常分布区间的异常值，其中正常分布区间为：

[𝑄1 − 1.5 × 𝐼𝑄𝑄，𝑄3 + 1.5 × 𝐼𝑄𝑄]

4

 

之后，求得去除异常值之后日销量的平均值，并用该平均值替换异常值，从而获得异常值处理之后的单品蔬菜日销量数据。可以从花叶类蔬菜周销量随时间变化的图中，看出替换异常值前后的效果变化。如下图所示，用黑色线条来描绘替换异常值之前的数据，用绿色线条来描绘替换异常值之后的数据。可以发现替换异常值之后，周销量数据明显变得更加平滑。

图1 花叶类蔬菜日销量箱线图

图2 数据预处理前后花叶类蔬菜周销量时间序列对比图

4.2  蔬菜类商品不同品类的分布规律及相互关系

          本部分将先从总体的角度去分析不同品类蔬菜的分布规律及相互关系，之后认为再从周、月、年等多个维度详细分析不同品类蔬菜的分布规律及相互关系。

4.3  不同品类蔬菜的总体分布规律及相互关系

本节使用三种方法分析不同品类蔬菜的总体分布规律及相互关系。首先，从 K-S 检验的角度分析不同品类蔬菜的销量是否属于同一分布；之后，使用皮尔逊系数矩阵分析不同品类蔬菜的销量之间的相关性；最后，从ARIMA模型的角度分析单一品类蔬菜的历史销量的分布规律。

 

4.3.1 K-S检验

使用K-S检验的方法分别检验各蔬菜品类两两之间的销量是否属于同一分布。本节从日销量和月销量的角度，分析了各品类蔬菜销量分布之间的关系。首先，将各蔬菜品

类每日的销售流水加总，获得各蔬菜品类每日的销售总量，之后分别两两组合进行K-S检验，共进行15次检验。

          检验步骤如下（以花叶类蔬菜与水生根茎类蔬菜的日销量分布为例）： Step1）提出假设
          原假设H0:花叶类蔬菜与水生根茎类蔬菜的日销量样本来自于同一分布。      被择假设H1:花叶类蔬菜与水生根茎类蔬菜的日销量样本来自于不同分布。

Step2）构造检验统计量

                                                                (1)

          其中，𝑓𝑚(𝑤)为花叶类蔬菜日销量的观察样本序列值，𝑓𝑚(𝑤)为水生根茎类蔬菜日销量的观察样本序列值。

Step3）计算并分析结果

          通过R语言代码，得到以下结果：
          如图所示，K-S 检验的 p-value 小于 0.001，因此有充足的把握拒绝原假设 H0:花叶类蔬菜与水生根茎类蔬菜的日销量样本来自于同一分布。

Step4）对其他组合进行检验
          对于其他品类蔬菜的组合，观察结果可以发现，K-S 检验的 p-value 均小于 0.001，因此有充足的把握拒绝各蔬菜品类之间的日销售量属于同一分布。

由于日销量存在较大的随机性，而月销量则相对消除了一定的偶然因素影响，因此

针对各品类蔬菜的月销量进行了K-S检验。结果显示，花菜类与水生根茎类的月销量之间 K-S 检验的 p-value 为 0.2106，没有充足的把握拒绝其月销量属于同一分布；除该组合之外，各品类蔬菜的月销量两两之间均不属于同一分布。

图3 花菜类蔬菜与水生根茎类蔬菜的月销量样本K-S检验结果

4.3.2 皮尔逊相关系数

使用皮尔逊相关系数来判断各蔬菜品类销量之间的相关性，并使用热力图将其可视

化。同样，本段从日销量和月销量的角度，分析各品类蔬菜销量之间的相关系数。步骤如下：

Step1）获得日销量和月销量

将各蔬菜品类的每日销量流水加总获得日销量。由于日销量具有一定的随机性，因

此又选取了月销量作为研究对象。此外，部分蔬菜品类缺少部分日销量数据，认为这是因为当日该品类蔬菜没有售出，因此用0代替。

Step2）计算皮尔逊相关系数
          皮尔逊相关系数可以用来度量两个变量之间的相关程度，其计算公式为：

(2)

          其中，𝑋𝑖和𝑋𝑖分别表示两个蔬菜品类的日（月）销量样本序列值，而X ̅和Y ̅则表示对应序列的样本均值。

通过R语言代码，得到以下结果：

图4 各品类蔬菜日总销量相关系数矩阵

图5 各品类蔬菜月总销量相关系数矩阵

Step3）画出相关系数热力图
            通过R语言代码，将相关系数矩阵以热力图的方式进行可视化：

 

图6 各品类蔬菜日总销量相关系数热力图

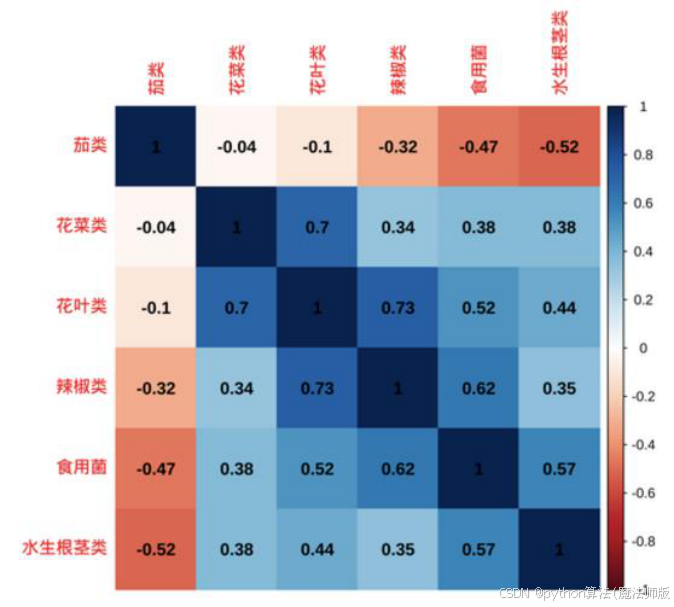
图7 各品类蔬菜月总销量相关系数热力图

          结合两图发现，花叶类与辣椒类、辣椒类与食用菌类之间的相关系数的绝对值较大，具有较强的相关性；除此之外，其余蔬菜品类间的相关性并不明显。

4.3.3 ARIMA时间序列分析

          对于蔬菜类商品同一品类内部的销量分布规律，使用ARIMA模型进行时间序列分析。ARIMA 模型的基本思想是利用数据本身的历史信息来预测未来，主要由三部分构成，分别为自回归模型（AR）、差分过程（I）和移动平均模型（MA）。对于ARIMA(p,d,q)模型中的三个参数，其中：
          p 表示自回归模型部分，描述了模型中使用观测值的滞后值，即认为观测值是它前面的p个观测值的线性组合；
          q 表示移动平均模型部分，描述了模型中使用的错误项的滞后值，即认为观测值是它前面的q个白噪声的线性组合；

 

          d表示差分过程部分，描述了差分的阶数，即将进行d阶差分之后的时间序列数据代入ARMA模型进行拟合。当d=0时，其数学表达式为：

(3)

          本节中对各品类蔬菜的周销量进行ARIMA时间序列分析的步骤如下：
Step1）获得周销量
          由于日销售量具有较大的偶然性，因此将各品类蔬菜的周销量作为研究对象。将各品类蔬菜每周的销售流水加总，获得各品类蔬菜的周销量。

Step2）根据图像分析
          以水生根茎类蔬菜为例：首先，将水生根茎类蔬菜每周的销量流水加总，获得该品

类蔬菜的周销量，并画出其时间序列图像。从时间序列图像中可以看出，水生根茎类蔬

菜售量的变化具有一定的季节性。结合生活经验，以一年为周期，并作出其ACF图像、PACF图像等以观察ARIMA模型的参数特征与拟合效果。可以发现，PACF图像呈现较好的截尾状态，但ACF并没有随滞后阶数增大而逐渐接近于0；因此用ARIMA模型并不能较好地拟合该时间序列。

Step3）获得数学表达式
          之后，使用 R 语言程序自动确定 ARIMA 模型的相关参数，可以获得ARIMA(0,0,1)(0,1,1)[52]模型。读取代码结果，可以分析出水生根茎类蔬菜周销量的数学表达式为：

                                                                                        (4)

图8 水生根茎类蔬菜周销量的时间序列图像

 

图9 水生根茎类蔬菜周销量的时间序列图像

Step4）模型评价与检验
          可以从R语言程序代码结果中获取对于该模型拟合效果的评价指标，如该模型的赤池信息准则AIC为1322.4，而该因素可以衡量ARIMA模型的拟合优度和复杂度。一般而言，比较不同的模型，AIC值越小，其模型效果越好。此外，还有BIC、对数似然值等信息去评价该模型。综合这些数据，认为ARIMA模型并不能较好的反映水生根茎类蔬菜的周销量分布规律。

图10 水生根茎类蔬菜周销量的PACF图像

图11 水生根茎类蔬菜周销量ARIMA模型结果

library("readxl") library("forecast") a = read_excel(path = "附件1.xlsx", sheet = "Sheet1") b = read_excel(path = "附件2.xlsx", sheet = "Sheet1") c = read_excel(path = "附件3.xlsx", sheet = "Sheet1") d = read_excel(path = "附件4.xlsx", sheet = "Sheet1") correspond=a[,c(1,3)] library(showtext) showtext_auto() library(dplyr) library("data.table") correspond=data.table(correspond) setkey(correspond,单品编码) bt=data.table(b) setkey(bt,单品编码) b_1=bt[correspond] b_2=aggregate((`销量(千克)`)~(分类编码+销售日期),data=b_1,FUN = sum) b_2_11=b_2[b_2$分类编码=="1011010101",] #之后会对比改进前的时间序列分析 ## 对每个单品的异常值处理(数据预处理) mylist=unique(b_1$单品编码) #获得所有蔬菜单品的编码 b_i=b_1[b_1$单品编码==mylist[1],] b_i_1=aggregate((`销量(千克)`)~(单品编码+销售日期),data=b_i,FUN = sum) #获得第一个蔬菜的每天的售量之和 remove_outlier=function(x){  names(x)[3]="a"  q1=quantile(x$a)[[2]]  q2=quantile(x$a)[[3]]  q3=quantile(x$a)[[4]]  iqr=q3-q1  minq=q1-1.5*iqr  maxq=q3+1.5*iqr  x$a[x$a>maxq|x$a<minq]=NA  x$a[is.na(x$a)]=mean(x$a,na.rm=TRUE)  names(x)[3]="销量(千克)"  return(x) } b_i_1=remove_outlier(b_i_1) bb=b_i_1 for(ii in 2:251){  b_i=b_1[b_1$单品编码==mylist[ii],]

 

if(nrow(b_i)!=1){  b_i=aggregate((`销量(千克)`)~(单品编码+销售日期),data=b_i,FUN = sum)  b_i=remove_outlier(b_i)  bb=rbind(bb,b_i)  }else{  b_i=b_i[,c(3,1,4)]  bb=rbind(bb,b_i)  } } b_i11=aggregate((`销量(千克)`)~(单品编码+销售日期),data=b_1,FUN = sum) rm=bb rm=na.omit(rm) #write.csv(rm,"remove.outlier.csv") ## 改进后的时间序列分析 rmt=data.table(rm) setkey(rmt,单品编码) b_1=rmt[correspond] b_2=aggregate((`销量(千克)`)~(分类编码+销售日期),data=b_1,FUN = sum) b_2_1=b_2[b_2$分类编码=="1011010101",] b_2_2=b_2[b_2$分类编码=="1011010201",] b_2_3=b_2[b_2$分类编码=="1011010402",] b_2_4=b_2[b_2$分类编码=="1011010501",] b_2_5=b_2[b_2$分类编码=="1011010504",] b_2_6=b_2[b_2$分类编码=="1011010801",] sxfx=function(x){  b_sxfx=x  b_sxfx$销售日期1=as.Date(b_sxfx$销售日期)  sales <- b_sxfx[, 3]  dates <- b_sxfx[, 4]    dates <- as.Date(dates)    weekly_sales <- data.frame(Week = format(dates, "%Y-%W"), Sales = sales) %>%  group_by(Week) %>%  summarise(TotalSales = sum(Sales))  #按周进行加总 再进行ARIMA分析  myts <- ts(weekly_sales[, 2], frequency = 52)  #plot(myts)  #acf(myts)  #pacf(myts)  fit <- auto.arima(myts,seasonal=TRUE)  myts <- ts(weekly_sales[, 2], frequency = 1)  plot(myts,xlab="Week",ylab="Total sales per week")  summary(fit) }

 

sxfx(b_2_1) sxfx(b_2_11) sxfx(b_2_2) sxfx(b_2_3) sxfx(b_2_4) sxfx(b_2_5) sxfx(b_2_6) ## 品类、按日、总销量算corr并画热力图 b21=b_2_1$`(\`销量(千克)\`)` b22=b_2_2$`(\`销量(千克)\`)` b23=b_2_3$`(\`销量(千克)\`)` b24=b_2_4$`(\`销量(千克)\`)` b25=b_2_5$`(\`销量(千克)\`)` b26=b_2_6$`(\`销量(千克)\`)` length(b21) length(b22) b22=c(b22,0) length(b23) length(b24) b24=c(b24,rep(0,35)) length(b25) length(b26) bbb=data.frame(花叶类=b21,  花菜类=b22,  水生根茎类=b23,  茄类=b24,  辣椒类=b25,  食用菌=b26) cor(bbb) library(corrplot) # 基础可视化-定量变量（相关性热图） bbb %>%  select_if(is.numeric) %>%  cor() %>%  corrplot(method = 'color', order = 'AOE', addCoef.col = 'black') ## 品类、按月、总销量corr并画热力图 b_2$月份 <- format(b_2$销售日期, "%Y-%m") monthly_sales <- aggregate(`(\`销量(千克)\`)` ~ (分类编码+月份), b_2, sum) bb_2=monthly_sales bb_2_1=bb_2[bb_2$分类编码=="1011010101",] bb_2_2=bb_2[bb_2$分类编码=="1011010201",]