2023年高教社杯全国大学生数学建模竞赛题目E题黄河水沙监测数据分析

小浪底水库最优监测方案研究

基于小波变换和背包模型的小浪底水库最优监测方案研究

本文针对黄河小浪底水库的水沙通量变化趋势及最优监测方案进行了研究。

        首先,对附件1、附件2、附件3的数据进行了整理，使用python软件对大量的缺失数据采用平均值进行了填补。

针对问题(1), 首先，研究含沙量与时间的关系,得出结论：一是2016、2017年的含沙量较小,但从2018年开始大幅度增长，含沙量随着年份存在周期性波动。二是每年2、3季度为旺季,每年1、4季度为淡季。三是建立了含沙量随时间（日）变化的正弦函数。其次,分别建立了含沙量与水位、水流量的双对数回归方程，得出结论：水位每增加1%,含沙量增加36.31%；水流量每增加1%,含沙量增加1.06%。第三，估算出年均水流量324亿m 3,年均总排沙量2亿吨。

针对问题(2),把数据整理成以“月”为时间点的时间序列，首先，描述性分析得出结论：各月水流量分化严重，但平均波动幅度较小，排沙量则相反。其次，季节性分析得出结论：水通量和沙通量都在每年7月比例最大，在1月占比最小；水通量、沙通量每年6月-10月是旺季,每年1月-3月、11月、12月是淡季。第三，周期性分析得出结论：水沙通量的周期为365天, 2018年有突变现象。第四，使用M-K 检验法进行突变性分析得出结论：从t=30开始出现显著的上升趋势,在t=27时出现突变点。再使用Fisher最优分割法进行验证，得出的结论与M-K法检验法一致。第五，为了详细而准确地寻找水沙通量的周期性和突变点，还使用小波变换分析法得出结论：水通量、沙通量均以20月为周期振荡，呈现了5次正负循环交替，出现了8个突变点。

针对问题(3)，首先，使用R/S分析法研究水沙通量是否在未来2年存在相同趋势、反转趋势或随机趋势。把全时段2016-2021年分为2个阶段，第一阶段（2016-2017年）用于检验，第二阶段（2018-2021年）用于预测，检验结果表明：R/S分析法具有一定的可靠性，可以用于预测，预测结果表明：水沙通量未来变化将出现反转趋势。其次，分别针对水通量、沙通量建立了傅里叶级数，预测出未来2年的水沙通量数据。第三，借用背包问题建立了0-1规划模型，获得了未来2年最优的采样监测方案。

针对问题(4),首先，使用“微元法”计算平均河底高程，观察其变化情况得出结论：每年“调水调沙”成效不佳，河底高程始终保持在45m左右，2019年成效尤其不佳，下降了0.23m。其次，考察水通量的变化情况得出结论：每年“调水调沙”成效不佳，水通量呈现逐年下降趋势，2018年成效尤其不佳，水通量下降了72%。如果不“调水调沙”，那么水通量逐年上升趋势越来越严重，2022年水通量上升幅度尤其不佳，上升了6.4%。第三，考察沙通量的变化情况得出结论：每年“调水调沙”成效不佳，2021年与2020年相比，沙通量下降了45.4%。第四，使用灰色GM（1,1）模型预测了未来十年的河底高程。

本文优点是使用季节指数、双对数回归方程、M-K 检验法、最优分割法、小波变换法、R/S分析法研究分析季节性、周期性、突变性，能够交叉验证，可靠性强；使用傅里叶级数逼近水沙通量曲线预测精度较高；在建立最优采样监测方案时巧妙转化为背包问题，存在最优解；在计算曲线的平均高度时，使用了“微元法”。不足之处是在预测未来2年的水沙通量时，难以给出突变点数值，导致在突变点处误差较大。

        本文所使用的模型或方法可以推广到水文资料分析问题中，还可以推广到其它有关季节性、周期性、突变性等问题的分析中。

关键词：双对数回归；M-K检验；小波变换；R/S分析；傅里叶级数；0-1规划；微元法

                                                              一、问题重述

通过研究黄河水沙通量的变化规律可以对沿黄流域的环境治理、气候变化和人民生活的影响做出一定判断,以及对优化黄河流域水资源分配、协调人地关系、调水调沙、防洪减灾提供帮助。对黄河的治理发展有重要的理论指导意义。

根据附件中的数据,建立数学模型,解决下列问题：
（1）研究含沙量与时间、水位、水流量的关系,并估算近6年的年总水流量和年总排沙量。

（2）分析水沙通量的突变性、季节性和周期性等特性,研究水沙通量的变化规律。

（3）根据水沙通量的变化规律,预测该水文站未来两年水沙通量的变化趋势,并为该水文站制订未来两年最优的采样监测方案,使其既能及时掌握水沙通量的动态变化情况,又能最大程度地减少监测成本资源。

        （4）分析每年 6-7 月小浪底水库进行“调水调沙”的实际效果。如果不进行“调水调沙”,10 年以后该水文站的河底高程将会带来什么结果和影响。

二、问题分析

首先,要对原始数据进行整理,主要是对空缺数据的补充。

针对问题(1),该问题分为两个方面,一是研究水位、水流量、时间与含沙量的关系,二是估算近六年的该水文站的年总流水量和年总排沙量。对于含沙量与时间的关系,可以通过时序图、季节指数、时间趋势等方法来描述。对于含沙量与水位的关系,可以通过相关分析、回归分析来解决。然后定义年总流水量和年总排沙量,并计算6年的数值结果。

针对问题(2),水通量就是径流量（亿m3），沙通量就是排沙量（亿吨），研究它们的变化规律，需要从统计特征、季节性、周期性和突变性四个方面来入手。季节性可通过月份指数、季度指数来描述。周期性可通过时序图、建立三角函数来解决。突变性可通过非参数 Mann-Kendall 检验法来解决。

针对问题(3),为预测水沙通量的变化趋势,我们借鉴R/S分析法分析水沙通量的分形特征和长期记忆过程,以判断其未来存在相同趋势、反转趋势或随机趋势。为了制订采样监测方案,使用小波分析法分析信号不同周期的时间演变规律,以掌握其丰枯旱涝情况,再根据这些情况制订最优的采样监测方案。

        针对问题(4),要评估“调水调沙”的实际效果，可以比较“调水调沙”前后河底高程、水沙通量、水流量等指标的变化。根据起点距的定义，使用“微元法”近似计算平均河底高程。

针对本文建立的模型,还需要进行敏感性分析和稳健性分析。

本文研究路径如图1所示。

三、符号说明

y：因变量 （含沙量）	x：自变量 （水位、时间、水流量）
：回归系数 1	：回归常数 0
z：表示年总水流量（亿m3）	1x ：水位
p：表示水通量（亿m 3）	tx(2) ：表示 时刻的水流量（m3/s）
q：表示沙通量（亿吨）	2x :水流量
f t ：表示t时刻的水沙通量	t：表示时刻（日）
tx ：表示t时刻的水沙通量	H：R/S分析法的统计量

注：其余符号在文中给出.

四、模型假设

为了简化问题,作如下假设：

（1）附件数据准确无误。

（2）水位和河底高程固定均以海拔72.26米为基准面。

（3） f t 表示t时刻的水沙通量，假设其满足狄利赫里（Dirichlet）条件。

（4）水通量、沙通量序列是独立序列。

（5）每年6-7月份“调水调沙”一次。

五、模型建立与求解

5.0数据整理

本文提供了以“日”“月”“年”为时间单位的时间序列。首先,检查日期是否连续,如果不连续,就补充完整。其次,由于数据存在缺失,就用邻近值代替。第三,为了排除闰年的影响,一年定为365天。附件

1的数据整理结果（样表）如表1所示。

表1 数据整理

序号	年	月	日	水位(m)	流量(m3/s)	含沙量kg/m3)
1	2016	1	1	42.79	357	0.825
2	2016	1	1	42.8	363	0.825
3	2016	1	1	42.8	363	0.796
4	2016	1	1	42.81	368	0.796
5	2016	1	1	42.84	384	0.796

…

2338

2016

12

30

42.19

217

0.415

5.1问题（1）——建立含沙量与时间、水位和水流量的关系

        问题分析：含沙量与时间的关系,可以通过时序图、季节指数、时间趋势等方法来描述。含沙量与水位、水流量的关系,可以通过相关性、建立回归方程来描述。

        建模思路：首先,研究含沙量与时间的关系,画时序图观察是否存在某种趋势,计算季节指数观察是否存在旺季和淡季。其次,以含沙量为因变量,以水位、水流量为自变量,建立回归方程。

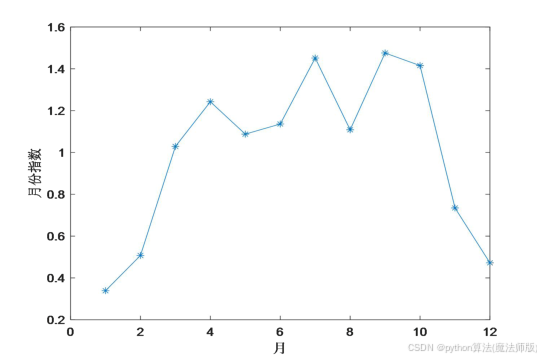
分别计算12个月的月份指数和4个季度的季度指数,如图4、图5所示,从图中可得出以下结论：（1）每年7月、9月、10月为旺季,每年1月、2月、11月、12月为淡季。
（2）每年2、3季度为旺季,每年1、4季度为淡季。

图4 含沙量的月份指数                              图5 含沙量的季度指数

5.1.1.2研究含沙量与时刻（日）的关系

使用最小二乘法进行分段拟合得,

拟合效果如图6、图7所示,从图中可知,拟合精度较高。

图6 2016-2017年含沙量函数拟合效果                图7 2018-2021年含沙量函数拟合效果

5.1.2研究含沙量与水位、水流量的关系

画出水位、水流量、含沙量两两之间的散点图,如图6所示。从图中可得出以下结论：

（1）水位与水流量之间是高度的线性正相关关系。

（2）水位与含沙量之间是线性正相关关系。

（3）水流量与含沙量之间是线性正相关关系。

        基于以上结论,可分别建立含沙量与水位、含沙量与水流量的回归方程,但不能以水位、水流量为自变量建立二元回归模型,这是因为水位与水流量高度相关的缘故。

图8 水位、水流量、含沙量的散点图

5.1.2.1一元线性回归模型简介

 

5.1.2.2含沙量与水位的回归方程

设 y表示含沙量（kg/m 3）,

1x 表示水位（m）, y和

1x 的双对数回归模型为

（6）

ln

y



 0



 1

ln

x 1





使用MATLAB软件,给定显著性水平0.05,使用最小二乘法进行参数估计,结果如表2所示。

 

画出带有正态分布概率曲线的标准化残差直方图,如图9所示,从图中可知,残差服从均值为0的正态

6

分布。

        以标准化预测值为横坐标,以标准化残差为纵坐标,画散点图,如图10所示,从图中可知,残差随机分布在 3 以内,且没有明显的趋势,表明残差的标准差是常数,且相互独立。

根据式（7）可以得出以下结论：

（1）含沙量与水位是正相关关系。

（2）水位每增加1%,含沙量增加36.31%,含沙量对水位的变化非常敏感。

from 格式转换类 import wk_format

for year in range(2016, 2022):

wk_format(year)

from openpyxl import Workbook, load_workbook

def wk_format(year):

new_wk: Workbook = Workbook()

new_sheet = new_wk.active

old_wk: Workbook = load_workbook("待整理数据表格.xlsx", data_only=True)

for row in old_wk.get_sheet_by_name(str(year)):

cell_list = []

for cell in row:

cell_list.append(cell.value)

new_sheet.append(cell_list)

new_wk.save(f"{year}.xlsx")

from pyecharts.charts import Bar

from pyecharts.options import *

from 统计工具类 import *

bar = Bar()

x = ['2016', '2017', '2018', '2019', '2020', '2021']

a, b = sum_utils()

y = a

for i in range(len(y)):

y[i] = y[i] / 100000000

bar.add_xaxis(x)
bar.add_yaxis("年总水流量(亿立方米)", y, label_opts=LabelOpts(is_show=True, position="top")) # 全局设置

bar.set_global_opts(

      legend_opts=LegendOpts(is_show=True, pos_top='2%'),
      title_opts=TitleOpts(title=f"2016-2021各年总水流量", pos_left='center', pos_bottom='2%')）bar.render("年总水流量图.html")

from pyecharts.charts import Bar

from pyecharts.options import *

from 测试代码.年总量计算类.统计工具类 import sum_utils

bar = Bar()

x = ['2016', '2017', '2018', '2019', '2020', '2021']

a, b = sum_utils()

y = b

bar.add_xaxis(x)
bar.add_yaxis("年总输沙量(亿吨)", y, label_opts=LabelOpts(is_show=True, position="top")) for i in range(len(y)):

y[i] = y[i] / 100000000

bar.set_global_opts(

      legend_opts=LegendOpts(is_show=True, pos_top='2%'),
      title_opts=TitleOpts(title=f"2016-2021各年总输沙量", pos_left='center', pos_bottom='2%')) bar.render("年总输沙量图.html")

import decimal

from math import floor

from openpyxl import Workbook, load_workbook

def get_sum(year):

wk: Workbook = load_workbook(f'{year}年日平均计算.xlsx')

sheet = wk.active

sum1 = decimal.Decimal('0.0000')

sum2 = decimal.Decimal('0.0000')

for cell in sheet['G2:G361']:

sum1 += decimal.Decimal(cell[0].value)

for cell in sheet['H2:H361']:

sum2 += decimal.Decimal(cell[0].value)

return floor(sum1), floor(sum2)

def sum_utils():

sum_list1 = []

sum_list2 = []

for year in range(2016, 2022):

value1, value2 = get_sum(year)

sum_list1.append(value1)

sum_list2.append(value2)

return sum_list1, sum_list2

from 日平均计算类 import day_start

from 月平均计算类 import month_start

from 折线图处理类 import line_start

for year in range(2016, 2022):

day_start(f'{year}.xlsx')

month_start(year)

line_start(year)

from openpyxl import Workbook, load_workbook

import decimal

def day_start(file):wk: Workbook = load_workbook(file, data_only=True)

sheet = wk.active

prev_d = 1

prev_m = 1

count = decimal.Decimal('0.0')

water_level_sum = decimal.Decimal('0.00')

flow_sum = decimal.Decimal('0.00')

sand_content_sum = decimal.Decimal('0.00')

new_wk = Workbook()

new_sheet = new_wk.active
new_sheet.append(['年', '月', '日', '平均水位', '平均流量', '平均含沙量', '径流量(立方米)', '输沙量(吨)']) flag = True

for row in sheet:

if flag:

flag = False

continue

year = row[1].value

month = row[2].value

day = row[3].value

water_level = row[4].value

flow = row[5].value

sand_content = row[6].value
water_level = decimal.Decimal(water_level).quantize(decimal.Decimal('0.000')) flow = decimal.Decimal(flow).quantize(decimal.Decimal('0.000'))
sand_content = decimal.Decimal(sand_content).quantize(decimal.Decimal('0.000')) if prev_d != day:

water_level_sum = water_level_sum / count

flow_sum = flow_sum / count

sand_content_sum = sand_content_sum / count

runoff_sum = flow_sum * 3600 * 24

sediment_load_sum = sand_content_sum * flow_sum * 3600 * 24 / 1000

new_sheet.append(
      [year, prev_m, prev_d, water_level_sum, flow_sum, sand_content_sum, runoff_sum, sediment_load_sum]) prev_d = day

prev_m = month

water_level_sum = decimal.Decimal(water_level)

flow_sum = decimal.Decimal(flow)

sand_content_sum = decimal.Decimal(sand_content)

count = decimal.Decimal('1.0')