目录
3. Information Analysis(IC 分析)
5. Rank Autocorrelation(因子稳定性)
一、Load Data 加载数据
首先需要安装对应的库
! pip install alphalens-reloaded
# 原版已不再维护,推荐使用“社区重载版(alphalens-reloaded)”
import warnings
warnings.filterwarnings('ignore')
from pathlib import Path
import pandas as pd
from alphalens.tears import create_summary_tear_sheet
from alphalens.utils import get_clean_factor_and_forward_returns
idx = pd.IndexSlice
with pd.HDFStore('data.h5') as store:
lr_predictions = store['lr/predictions']
lasso_predictions = store['lasso/predictions']
lasso_scores = store['lasso/scores']
ridge_predictions = store['ridge/predictions']
ridge_scores = store['ridge/scores']
# DATA_STORE = Path('..', 'data', 'assets.h5')
DATA_STORE = Path('data', 'assets.h5') # change to the real path 修改到真实路径
def get_trade_prices(tickers, start, stop):
prices = (pd.read_hdf(DATA_STORE, 'quandl/wiki/prices').swaplevel().sort_index())
prices.index.names = ['symbol', 'date']
prices = prices.loc[idx[tickers, str(start):str(stop)], 'adj_open']
return (prices
.unstack('symbol')
.sort_index()
.shift(-1)
.tz_localize('UTC'))
def get_best_alpha(scores):
return scores.groupby('alpha').ic.mean().idxmax()
def get_factor(predictions):
return (predictions.unstack('symbol')
.dropna(how='all')
.stack()
.tz_localize('UTC', level='date')
.sort_index()) 注意文件路径要选对:数据来源于前面几节
# DATA_STORE = Path('..', 'data', 'assets.h5')
DATA_STORE = Path('data', 'assets.h5') # change to the real path 修改到真实路径
get_trade_prices 函数:
功能:从 HDF5 数据存储中读取股票的历史价格数据,并返回指定时间段和调整后的开盘价。
get_best_alpha 函数:
功能:从一组分数中选择最佳的 alpha 值。
get_factor 函数:
功能:处理预测数据,将其转换为因子格式,并进行一些数据清洗和格式化。
二、Linear Regression 线性回归
lr_factor = get_factor(lr_predictions.predicted.swaplevel())
lr_factor.head()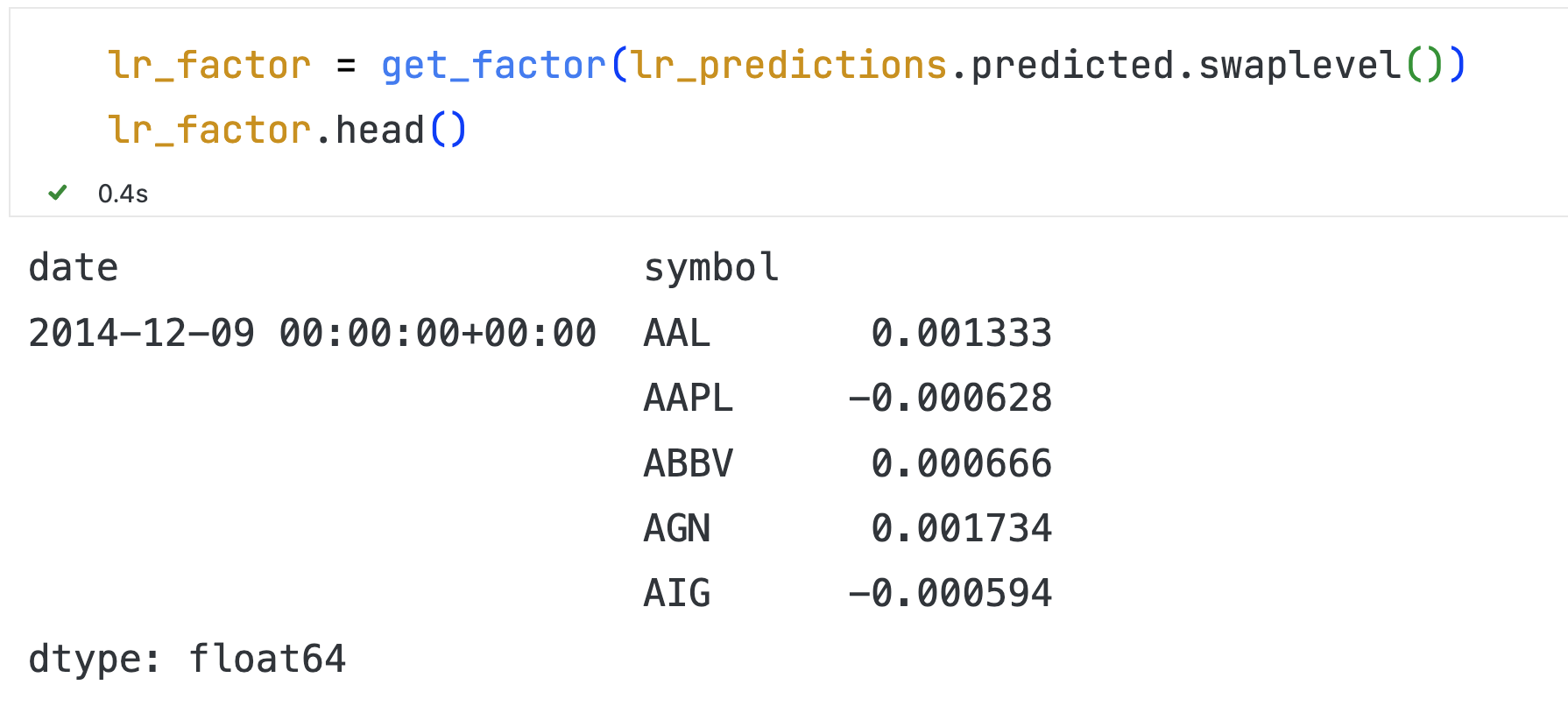
tickers = lr_factor.index.get_level_values('symbol').unique()
trade_prices = get_trade_prices(tickers, 2014, 2017)
trade_prices.info()

lr_factor_data = get_clean_factor_and_forward_returns(factor=lr_factor,
prices=trade_prices,
quantiles=5,
periods=(1, 5, 10, 21))
lr_factor_data.info()结果:
Dropped 0.0% entries from factor data: 0.0% in forward returns computation and 0.0% in binning phase (set max_loss=0 to see potentially suppressed Exceptions).
max_loss is 35.0%, not exceeded: OK!
<class 'pandas.core.frame.DataFrame'>
MultiIndex: 73812 entries, (Timestamp('2014-12-09 00:00:00+0000', tz='UTC'), 'AAL') to (Timestamp('2017-11-29 00:00:00+0000', tz='UTC'), 'XOM')
Data columns (total 6 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 1D 73812 non-null float64
1 5D 73812 non-null float64
2 10D 73812 non-null float64
3 21D 73812 non-null float64
4 factor 73812 non-null float64
5 factor_quantile 73812 non-null int64
dtypes: float64(5), int64(1)
memory usage: 3.7+ MB画图并分析
Alphalens 的 create_summary_tear_sheet 负责把单个因子拆成 5 组(quantiles)做业绩/IC/换手分析
create_summary_tear_sheet(lr_factor_data);
# 说明可以参考:alphalens入门篇 https://blog.csdn.net/u011331731/article/details/88314459
# 分析结论:短线有点信号,长线更稳,但都不强; turnover 高,费用吃利润,适合当排序信号,不适合单独对冲。Quantiles Statistics
| min | max | mean | std | count | count % | |
|---|---|---|---|---|---|---|
| factor_quantile | ||||||
| 1 | -0.043757 | 0.009896 | -0.002980 | 0.004034 | 14982 | 20.297513 |
| 2 | -0.014429 | 0.012193 | -0.000901 | 0.003243 | 14666 | 19.869398 |
| 3 | -0.012309 | 0.013843 | 0.000169 | 0.003228 | 14516 | 19.666179 |
| 4 | -0.011109 | 0.016001 | 0.001188 | 0.003352 | 14666 | 19.869398 |
| 5 | -0.009576 | 0.035734 | 0.003144 | 0.004032 | 14982 | 20.297513 |
Returns Analysis
| 1D | 5D | 10D | 21D | |
|---|---|---|---|---|
| Ann. alpha | 0.048 | 0.017 | 0.019 | 0.020 |
| beta | -0.017 | -0.068 | -0.058 | 0.041 |
| Mean Period Wise Return Top Quantile (bps) | 1.842 | 1.016 | 0.514 | 0.778 |
| Mean Period Wise Return Bottom Quantile (bps) | -1.847 | -0.613 | -0.910 | -1.259 |
| Mean Period Wise Spread (bps) | 3.689 | 1.652 | 1.433 | 2.028 |
Information Analysis
| 1D | 5D | 10D | 21D | |
|---|---|---|---|---|
| IC Mean | 0.019 | 0.017 | 0.019 | 0.023 |
| IC Std. | 0.178 | 0.165 | 0.172 | 0.156 |
| Risk-Adjusted IC | 0.107 | 0.100 | 0.111 | 0.148 |
| t-stat(IC) | 2.940 | 2.745 | 3.053 | 4.045 |
| p-value(IC) | 0.003 | 0.006 | 0.002 | 0.000 |
| IC Skew | -0.093 | 0.031 | -0.158 | -0.142 |
| IC Kurtosis | -0.212 | -0.053 | -0.107 | -0.231 |
Turnover Analysis
| 1D | 5D | 10D | 21D | |
|---|---|---|---|---|
| Quantile 1 Mean Turnover | 0.300 | 0.527 | 0.630 | 0.747 |
| Quantile 2 Mean Turnover | 0.516 | 0.705 | 0.758 | 0.797 |
| Quantile 3 Mean Turnover | 0.560 | 0.739 | 0.773 | 0.807 |
| Quantile 4 Mean Turnover | 0.515 | 0.704 | 0.756 | 0.789 |
| Quantile 5 Mean Turnover | 0.302 | 0.530 | 0.637 | 0.741 |
| 1D | 5D | 10D | 21D | |
|---|---|---|---|---|
| Mean Factor Rank Autocorrelation | 0.817 | 0.551 | 0.401 | 0.236 |
<Figure size 640x480 with 0 Axes>
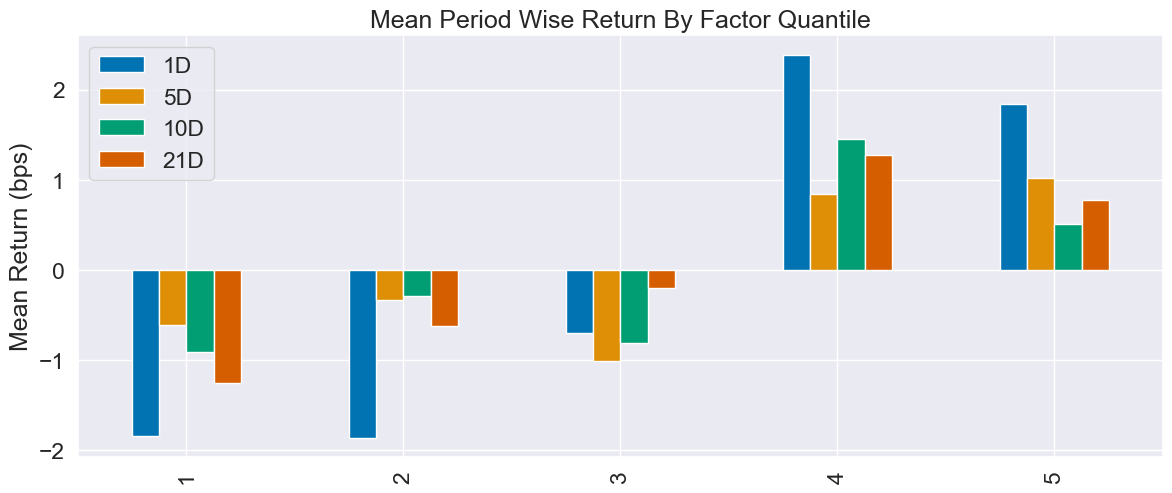
把单个因子拆成 5 组进行分析,通俗的例子就是:
因子值是“今天给学生按某科成绩排队”,
收益是“过几天再看他们总分涨了多少”,
拆 5 组就是“看看排在前面的学生是不是涨得最多”。
分析结论:短线有点信号,长线更稳,但都不强; turnover 高,费用吃利润,适合当排序信号,不适合单独对冲。
1. Quantiles Statistics(分组统计)
单调性良好:因子值从 Q1 到 Q5 递增,说明因子方向正确,没有反转。
2. Returns Analysis(收益分析)
alpha 低(<5%),beta 接近 0 ;市场中性,但超额收益也不高
多空对冲收益(spread) 1D 最高,但 5D/10D 下降,21D 略有回升。
收益不大,1D 的 3.7bps 扣掉交易成本(双边 ~2bps+滑点)后,净利很薄。
3. Information Analysis(IC 分析)
21D 的 IC 最高,t-stat 最显著(>4),说明因子在月度频率上更稳定。
但 IC 绝对值仍低于 0.03,属于“弱信号”,不能单独作为策略核心。
4. Turnover Analysis(换手率)
1D 换手率太高,双边 60%,扣掉费用后利润几乎被吃光。
21D 换手率相对可控,更适合实盘。
5. Rank Autocorrelation(因子稳定性)
短期因子排名稳定,适合短周期预测;
长期排名变化快,说明因子衰减快,不适合长周期持仓。
三、Ridge Regression 岭回归
类似的:
best_ridge_alpha = get_best_alpha(ridge_scores)
ridge_predictions = ridge_predictions[ridge_predictions.alpha==best_ridge_alpha].drop('alpha', axis=1)
ridge_factor = get_factor(ridge_predictions.predicted.swaplevel())
ridge_factor.head()
ridge_factor_data = get_clean_factor_and_forward_returns(factor=ridge_factor,
prices=trade_prices,
quantiles=5,
periods=(1, 5, 10, 21))
ridge_factor_data.info()
create_summary_tear_sheet(ridge_factor_data);结果:
Dropped 0.0% entries from factor data: 0.0% in forward returns computation and 0.0% in binning phase (set max_loss=0 to see potentially suppressed Exceptions).
max_loss is 35.0%, not exceeded: OK!
<class 'pandas.core.frame.DataFrame'>
MultiIndex: 73812 entries, (Timestamp('2014-12-09 00:00:00+0000', tz='UTC'), 'AAL') to (Timestamp('2017-11-29 00:00:00+0000', tz='UTC'), 'XOM')
Data columns (total 6 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 1D 73812 non-null float64
1 5D 73812 non-null float64
2 10D 73812 non-null float64
3 21D 73812 non-null float64
4 factor 73812 non-null float64
5 factor_quantile 73812 non-null int64
dtypes: float64(5), int64(1)
memory usage: 3.7+ MBQuantiles Statistics
| min | max | mean | std | count | count % | |
|---|---|---|---|---|---|---|
| factor_quantile | ||||||
| 1 | -0.037486 | 0.010285 | -0.003205 | 0.003644 | 14982 | 20.297513 |
| 2 | -0.011773 | 0.012590 | -0.001242 | 0.003003 | 14666 | 19.869398 |
| 3 | -0.009860 | 0.014102 | -0.000230 | 0.003023 | 14516 | 19.666179 |
| 4 | -0.008802 | 0.016130 | 0.000739 | 0.003175 | 14666 | 19.869398 |
| 5 | -0.007385 | 0.035124 | 0.002576 | 0.003867 | 14982 | 20.297513 |
Returns Analysis
| 1D | 5D | 10D | 21D | |
|---|---|---|---|---|
| Ann. alpha | 0.048 | 0.020 | 0.022 | 0.020 |
| beta | -0.018 | -0.074 | -0.065 | 0.038 |
| Mean Period Wise Return Top Quantile (bps) | 1.686 | 0.947 | 0.353 | 0.654 |
| Mean Period Wise Return Bottom Quantile (bps) | -2.010 | -0.639 | -1.074 | -1.285 |
| Mean Period Wise Spread (bps) | 3.696 | 1.612 | 1.441 | 1.937 |
Information Analysis
| 1D | 5D | 10D | 21D | |
|---|---|---|---|---|
| IC Mean | 0.019 | 0.017 | 0.020 | 0.021 |
| IC Std. | 0.179 | 0.167 | 0.174 | 0.156 |
| Risk-Adjusted IC | 0.108 | 0.103 | 0.114 | 0.137 |
| t-stat(IC) | 2.952 | 2.829 | 3.110 | 3.748 |
| p-value(IC) | 0.003 | 0.005 | 0.002 | 0.000 |
| IC Skew | -0.105 | 0.011 | -0.160 | -0.149 |
| IC Kurtosis | -0.175 | -0.024 | -0.091 | -0.244 |
Turnover Analysis
| 1D | 5D | 10D | 21D | |
|---|---|---|---|---|
| Quantile 1 Mean Turnover | 0.294 | 0.514 | 0.619 | 0.739 |
| Quantile 2 Mean Turnover | 0.507 | 0.697 | 0.752 | 0.795 |
| Quantile 3 Mean Turnover | 0.554 | 0.733 | 0.773 | 0.804 |
| Quantile 4 Mean Turnover | 0.509 | 0.698 | 0.757 | 0.786 |
| Quantile 5 Mean Turnover | 0.296 | 0.520 | 0.628 | 0.736 |
| 1D | 5D | 10D | 21D | |
|---|---|---|---|---|
| Mean Factor Rank Autocorrelation | 0.822 | 0.569 | 0.417 | 0.247 |
<Figure size 640x480 with 0 Axes>
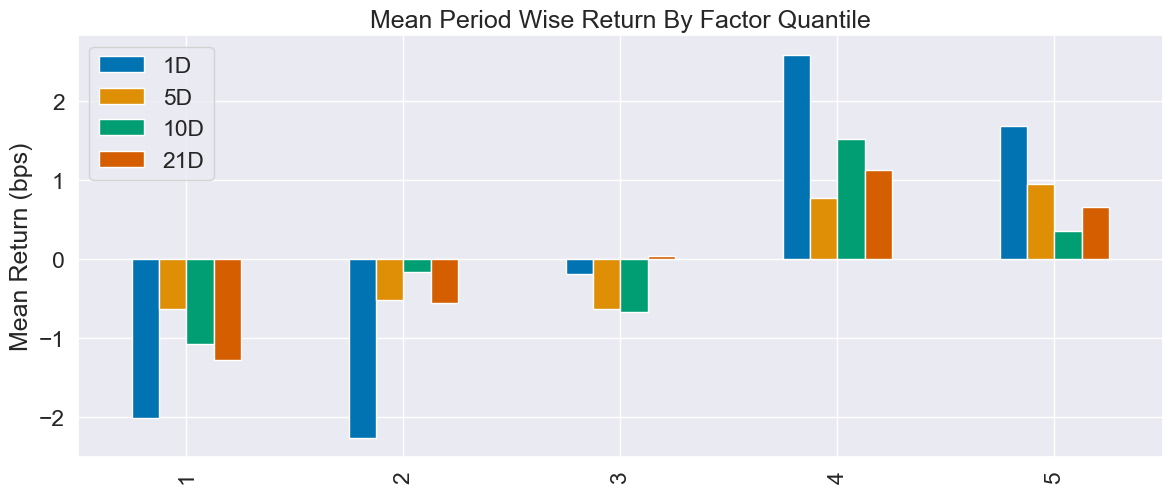
分析:
预测力:跟普通线性回归几乎打平,IC 同样“刚踩线”(0.019→0.021),t-stat 也没飞起来。
赚钱力:1D 对冲 spread 3.7 bps,跟 LR 一样“薄如纸”,扣完双边成本只剩 1 bps 左右。
稳定性:Rank 自相关更高(0.82),换手略低一点,说明岭回归“平滑”后,因子排名短期更耐操,但长周期照样衰减。
总结:岭回归只是“把 LR 的毛刺磨平”,没长出新增信息;成本端省 1 bps,收益端零提升,可留作候选
四、Lasso Regression 套索回归
代码,类似地:
best_lasso_alpha = get_best_alpha(lasso_scores)
lasso_predictions = lasso_predictions[lasso_predictions.alpha==best_lasso_alpha].drop('alpha', axis=1)
lasso_factor = get_factor(lasso_predictions.predicted.swaplevel())
lasso_factor.head()
lasso_factor_data = get_clean_factor_and_forward_returns(factor=lasso_factor,
prices=trade_prices,
quantiles=5,
periods=(1, 5, 10, 21))
lasso_factor_data.info()
create_summary_tear_sheet(lasso_factor_data);结果:
Dropped 0.0% entries from factor data: 0.0% in forward returns computation and 0.0% in binning phase (set max_loss=0 to see potentially suppressed Exceptions).
max_loss is 35.0%, not exceeded: OK!
<class 'pandas.core.frame.DataFrame'>
MultiIndex: 73812 entries, (Timestamp('2014-12-09 00:00:00+0000', tz='UTC'), 'AAL') to (Timestamp('2017-11-29 00:00:00+0000', tz='UTC'), 'XOM')
Data columns (total 6 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 1D 73812 non-null float64
1 5D 73812 non-null float64
2 10D 73812 non-null float64
3 21D 73812 non-null float64
4 factor 73812 non-null float64
5 factor_quantile 73812 non-null int64
dtypes: float64(5), int64(1)
memory usage: 3.7+ MBQuantiles Statistics
| min | max | mean | std | count | count % | |
|---|---|---|---|---|---|---|
| factor_quantile | ||||||
| 1 | -0.043925 | 0.010653 | -0.003470 | 0.004004 | 14982 | 20.297513 |
| 2 | -0.013494 | 0.012950 | -0.001383 | 0.003265 | 14666 | 19.869398 |
| 3 | -0.011373 | 0.014600 | -0.000327 | 0.003284 | 14516 | 19.666179 |
| 4 | -0.010174 | 0.016758 | 0.000706 | 0.003431 | 14666 | 19.869398 |
| 5 | -0.008641 | 0.035891 | 0.002654 | 0.004164 | 14982 | 20.297513 |
Returns Analysis
| 1D | 5D | 10D | 21D | |
|---|---|---|---|---|
| Ann. alpha | 0.048 | 0.017 | 0.019 | 0.020 |
| beta | -0.017 | -0.068 | -0.058 | 0.041 |
| Mean Period Wise Return Top Quantile (bps) | 1.842 | 1.016 | 0.514 | 0.778 |
| Mean Period Wise Return Bottom Quantile (bps) | -1.847 | -0.613 | -0.910 | -1.259 |
| Mean Period Wise Spread (bps) | 3.689 | 1.652 | 1.433 | 2.028 |
Information Analysis
| 1D | 5D | 10D | 21D | |
|---|---|---|---|---|
| IC Mean | 0.019 | 0.017 | 0.019 | 0.023 |
| IC Std. | 0.178 | 0.165 | 0.172 | 0.156 |
| Risk-Adjusted IC | 0.107 | 0.100 | 0.111 | 0.148 |
| t-stat(IC) | 2.940 | 2.744 | 3.053 | 4.045 |
| p-value(IC) | 0.003 | 0.006 | 0.002 | 0.000 |
| IC Skew | -0.093 | 0.031 | -0.158 | -0.142 |
| IC Kurtosis | -0.212 | -0.053 | -0.107 | -0.231 |
Turnover Analysis
| 1D | 5D | 10D | 21D | |
|---|---|---|---|---|
| Quantile 1 Mean Turnover | 0.300 | 0.527 | 0.630 | 0.747 |
| Quantile 2 Mean Turnover | 0.516 | 0.705 | 0.758 | 0.797 |
| Quantile 3 Mean Turnover | 0.560 | 0.739 | 0.773 | 0.807 |
| Quantile 4 Mean Turnover | 0.515 | 0.704 | 0.756 | 0.789 |
| Quantile 5 Mean Turnover | 0.302 | 0.530 | 0.637 | 0.741 |
| 1D | 5D | 10D | 21D | |
|---|---|---|---|---|
| Mean Factor Rank Autocorrelation | 0.817 | 0.551 | 0.401 | 0.236 |
<Figure size 640x480 with 0 Axes>
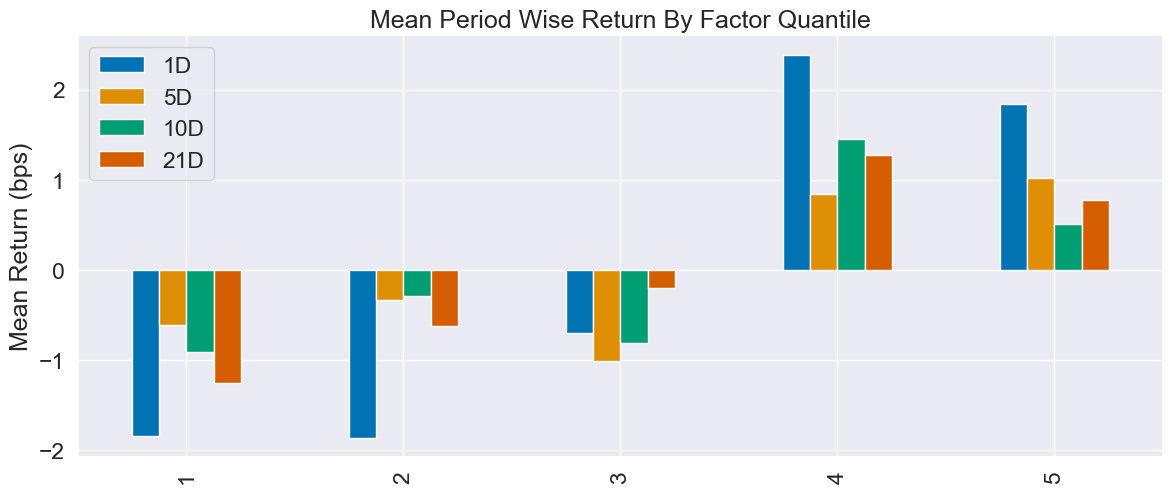
我的分析:
数字几乎跟普通线性回归重合,
Lasso 在这里只是“ LR 的影分身”,没有把任何变量真的压到 0,预测力、赚钱力、换手、衰减曲线几乎 1:1 复刻;正则化没起作用,说明原始特征里本来就没有明显冗余或共线。






















 1029
1029

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








