量子计算论文精讲 | SCIP求解MINLP问题

点击查看原文

内容简介

混合整数非线性规划(MINLP)是离散变量和连续变量混合的有限维非线性优化问题。很多实际问题可以建模成混合整数非线性规划问题，如能源生产和分配、物流、工程设计、制造以及化学和生物科学。SCIP是目前混合整数规划（MIP）和混合整数非线性规划（MINLP）最快的非商业求解器之一。SCIP求解器支持多种约束类型和目标函数类型，且可提供了丰富的插件接口，具有高效性、灵活性、可拓展性、易用性、开源性等特点，被广泛用于问题求解中。本次主要介绍两篇文章，第一篇主要关注SCIP中的基本算法、求解框架、设计原则。第二篇主要介绍SCIP在求解MINLP问题中如何处理非线性部分。

相关论文1

标题：Constraint integer programming
作者：Achterberg T

相关论文2

标题：SCIP: Global Optimization of Mixed-Integer Nonlinear Programs in a Branch-and-Cut Framework
作者：Vigerske S, Gleixner A
期刊: Optimization Methods and Software, 2018, 33(3): 563-593 

01 引言

SCIP（Solvers for Constraint Integer Programs），是一个开源的、高性能的数学优化软件包，用于解决约束整数规划（CIP）问题。具有高效性、灵活性、可拓展性、易用性、开源性等特点。CIP是用于解决在给定约束条件下，目标函数为整数变量的最优化问题。MINLP（ Mixed-Integer Nonlinear Programming ），混合整数非线性规划，目标函数和约束条件既包含连续变量，又包含整数变量，并且目标函数和约束条件中可能存在非线性项。目前的SCIP经过适当的扩展，已经可以处理MINLP问题，拓展的主要部分是将非线性处理加入SCIP的求解框架。本次主要分别介绍两部分内容来解SCIP求解MINLP的实现方法：

• SCIP求解机理

• SCIP与非线性处理的结合

02 SCIP求解机理

SCIP的基础算法

2.1 Branch and Bound

Branch and Bound的基本思想是将问题分解成一系列子问题，并通过剪枝策略来减少搜索空间，从而找到最优解。
Branch and Bound的求解流程：

1. 初始化：将问题分解成若干个子问题，并将它们放入一个待处理的队列中。
2. 选择：从队列中选择一个子问题进行处理。
3. 分支：将选中的子问题分解成若干个更小的子问题，并将它们放入队列中。
4. 限界：对每个子问题进行限界，即计算出一个上界和下界，用于判断该子问题是否有可能成为最优解。
5. 剪枝：根据限界结果，对不可能成为最优解的子问题进行剪枝，从而减少搜索空间。
6. 更新：如果找到了更优的解，则更新当前的最优解。
7. 终止：当队列为空时，算法终止，返回最优解。

Branch and Bound是一种穷举搜索的方法，这种方法的优点是可以找到全局最优解，但是在搜索空间较大时，计算复杂度会很高。

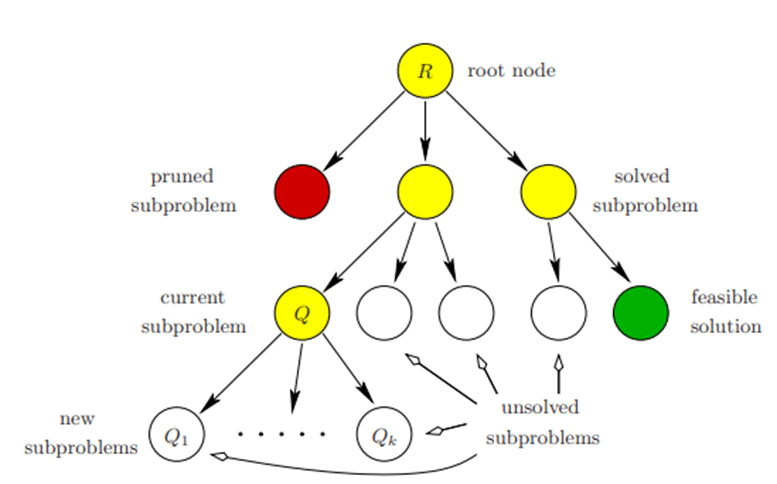
图1（来源：Constraint integer programming）

2.2 Cutting Planes

Cutting Planes算法的核心是不断添加线性不等式约束，这些约束可以通过线性规划求解得到。通过添加约束，Cutting Planes算法可以逐步缩小可行解空间，从而得到更精确的最优解。

下图使用Cutting Planes将带有分数的解x与Q整数点分开，从而得到QI。

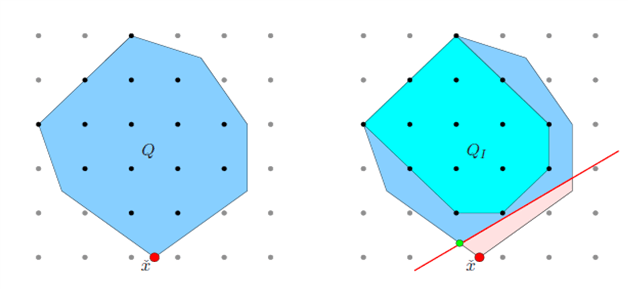
图2（来源：Constraint integer programming）

Branch and Bound的复杂度通常较高，特别是在搜索空间较大的情况下。而Cutting Planes通常在每次迭代中添加一个割平面约束，因此其复杂度通常较低。在实际应用中，Branch and Bound和Cutting Planes算法可以结合使用，例如使用Branch and Bound算法分解子问题，然后使用Cutting Planes算法对每个子问题进行求解。

2.3 Domain Propagation

Domain Propagation是根据当前问题的约束条件和变量的取值范围，推导出其他变量的取值范围，进而缩小问题的可行解空间。

比如，x1,x2,x3,x4需要满足互不相同的条件，那么如果x1,x2在g,b取值，x3,x4则只能再r,y取值。

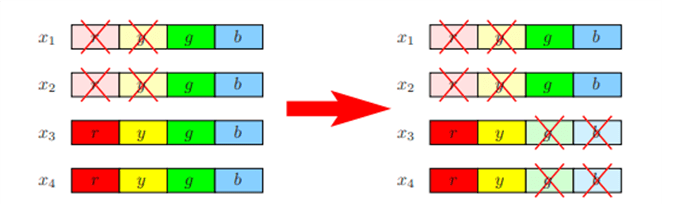
图3（来源：Constraint integer programming）

所以综合来看，在Branch and Bound中，Cutting Planes技术可以被用来加速搜索过程，因为它可以在每个子问题中添加额外的约束条件，从而减少搜索空间；Domain Propagation技术可以被用来缩小每个子问题的搜索空间。

03 SCIP与非线性处理的结合

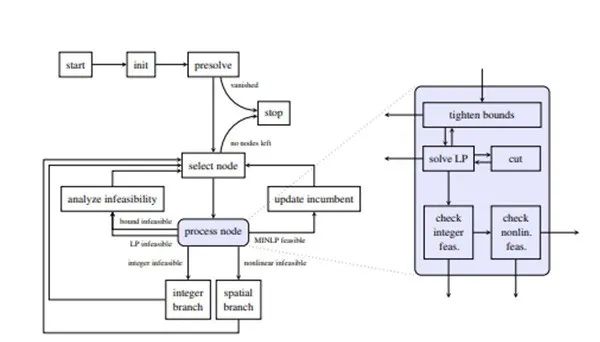
图4（来源：SCIP: Global Optimization of Mixed-Integer Nonlinear Programs in a Branch-and-Cut Framework）

图中显示了 SCIP 的主要求解循环，其中非线性约束的处理已嵌入其中。在求解过程中，SCIP通过引入辅助变量将可分解的非线性约束重新表述为基本非线性。在求解前，检测特殊的问题的数学结构和凸性，并将关键信息应用于边界收紧程序中。边界收紧过程中采取并解决 LP 松弛问题，它使用变量的局部边界重复更新。只要收紧 LP 松弛有足够的进展，这个切割循环就会迭代绑定收紧。分支首先在 LP 解决方案中具有分数值的整数变量上执行，随后对违反非凸约束中包含的变量执行。具体有以下内容：

3.1 Expression Graph

Expression Graph（表达式图）是一种数据结构和可视化工具，用于表示和管理问题中的数学表达式和约束。

Expression Graph是一个图形数据结构，通常是一个有向无环图，其中节点代表数学表达式的各个部分，边代表这些部分之间的依赖关系。每个节点可以表示变量、常数、运算符或函数等。这个数据结构的目的是将问题中的数学表达式分解为更小的组件，并明确表示它们之间的关系，以便更好地理解和处理这些表达式。

例如，如下图表达的是

其中，x,y取值范围是实数，z取值范围[0,1]

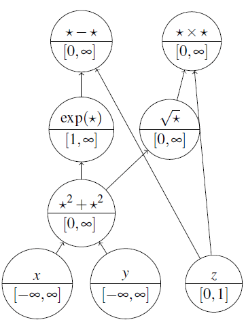
图5（来源：SCIP: Global Optimization of Mixed-Integer Nonlinear Programs in a Branch-and-Cut Framework）

3.2 Bound Tightening

在解决混合整数非线性规划（MINLP）问题时，"Constraint-Based Bound Tightening"（CBT，基于约束的边界紧束）和"Optimization-Based Bound Tightening"（OBBT，基于优化的边界紧束）都是用于改进问题界限的技术。

（1）Constraint-Based Bound Tightening (CBT，基于约束的边界紧束)：

CBT是一种用于缩小问题变量的取值范围的技术，通过考虑问题的约束条件来实现。具体来说，CBT通过以下方式工作：

• 约束分析：CBT会分析问题的约束条件，尤其是非线性约束。它试图找到与变量相关的约束条件，并推断出变量的取值范围。

• 边界更新:一旦分析出约束条件，CBT会使用这些信息来更新问题变量的上界和下界。这些边界的更新基于约束条件的有效性，以便更精确地表示问题的可行解空间。

• 界限传播： 更新的边界信息可以传播到其他相关变量，从而进一步缩小它们的取值范围。这可以通过约束条件之间的关系来实现。

如下图所示，将以下两个约束加入表达式图中，

找到与变量相关的约束条件，并推断出变量的取值范围。

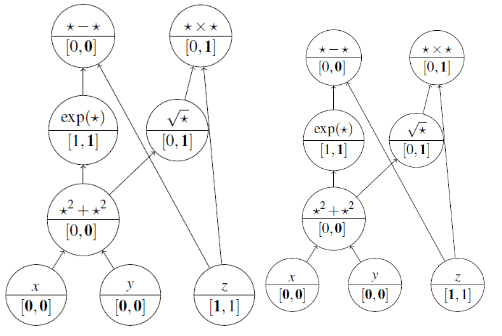
图6（来源：SCIP: Global Optimization of Mixed-Integer Nonlinear Programs in a Branch-and-Cut Framework）

（2）Optimization-Based Bound Tightening (OBBT，基于优化的边界紧束)：

OBBT是许多MINLP解算器的标准功能。默认情况下，SCIP在根节点应用OBBT以收紧全局边界。

OBBT算法通过分析问题结构和约束来改进变量的上下界。这可能包括以下几个方面：

线性化：对于非线性约束，OBBT可能尝试线性化这些约束，以获得更紧凑的线性界限。

凸化：对于非凸问题，OBBT可能尝试将问题分解为凸子问题，以获得更好的界限。

割平面添加：OBBT还可以添加割平面（cutting planes），这些平面可以进一步限制变量的可行范围。

变量约束推断：OBBT可以根据约束关系推断出变量之间的约束，从而改进变量的界限。

比如下图中，待解决的问题是：

通过增加两次线性约束以及割平面，将变量的可行范围缩小到阴影区。

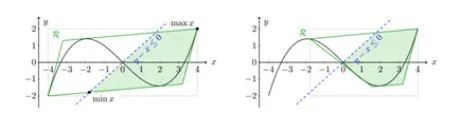
图7（来源：SCIP: Global Optimization of Mixed-Integer Nonlinear Programs in a Branch-and-Cut Framework）

此外，SCIP不仅利用找到的最优目标值来改进问题变量的界限，还利用对偶问题的解来学习有效的约束条件，这些约束条件在问题求解的后续搜索过程中非常有用。

3.3 Convexity Detection

检查约束的凹凸性有助于简化问题的求解过程，并提高求解效率。

对于一个复合函数 f(g(x))，其中 f (x)和 g(x) 都是两次可微（twice-differentiable）的函数。考察复合函数的二阶导数（second derivative）：

可以看出，如果 f(x) 是凸函数并且在区间 [g1,g2]单调递增（g1、g2分别为g(x)上下界），同时 g(x) 在区间[x1,x2]上是凸函数（x1、x2分别为x上下界），那么 f(g(x)) 在区间[x1,x2]上是凸函数。类似地，如果 f(x) 是凹函数并且在区间[g1,g2]上单调递增，同时 g(x) 在区间[x1,x2]上是凹函数，那么 f(g(x)) 在区间[x1,x2]上是凹函数。

这些条件允许我们通过函数的表达式图（expression graph）来传播凸性和凹性的性质。也就是说，如果我们能够确定复合函数中的各个组成部分（f 和 g）的凸性和凹性属性，然后通过这些属性来判断复合函数 f(g(x)) 在不同区间上的凸性和凹性。此外，还可以SCIP通过检查矩阵Q的最小特征值是否非负来检测二次约束的凸性

3.4 Linear Relaxation

在SCIP求解混合整数规划（MIP）问题时，如何构建和加强线性松弛问题（LP relaxation）的过程，以及在这个过程中如何添加有效的线性不等式（cuts）来改善松弛问题的界限都是需要斟酌的。切割条件和容差值的选择旨在平衡算法的效率和求解质量，以便更快地找到高质量的整数解。

具体实现方法包括通过凸包来识别函数的凸性、通过线性化割线来处理凸约束以及通过经典的McCormick松弛来处理二次项。

3.5 Reformulation

MINLP问题表述的重要性：与混合整数线性规划（MILP）不同，MINLP问题通常涉及非线性约束和目标函数。MINLP问题的数学表述对于问题的可解性和求解效率至关重要。不合适的表述可能导致问题非常难以求解。

重述表达式图时，根据子表达式的性质，有不同的替换规则：

     如果子表达式已知为凸或凹函数，则不进行替换。

     如果子表达式是二次函数、凸函数、凹函数或（带符号的）幂函数，SCIP会确保子表达式中的所有参数都对应于线性 表达式，方法是将非线性的参数替换为新的辅助变量，并添加新的约束以表示这些变量之间的关系。

     如果子表达式是多个项的乘积形式，SCIP会引入新的辅助变量和约束来表示这些乘积项，并用辅助变量的乘积来替代原始子表达式。

     如果子表达式是多个项的和的形式，SCIP会引入新的辅助变量和约束来表示这些和式，并用辅助变量的和来替代原始子表达式。

3.6 Branch

在求解混合整数非线性规划（MINLP）问题时，当一个松弛解不满足整数约束或非线性约束时，SCIP采用的变量分支策略。以下是详细措施：

1）整数变量分支： 如果发现一个分数（即非整数）的整数变量（即不属于整数集合），那么SCIP会执行整数变量分支。这意味着SCIP尝试将这个分数变量分支成两个整数分支，以尝试找到更好的解。

2）空间分支（Spatial Branching）：如果当前的松弛解是整数的，但违反了非线性约束，那么SCIP会执行空间分支。在这种情况下，SCIP尝试通过调整非线性约束中的某个出现在违反约束中的变量来改善解。这种分支策略是层级的，根据约束类型分别处理。

3.7 Primal Heuristics

在解决混合整数非线性规划（MINLP）问题时，SCIP使用的一系列启发式算法，这些算法有助于寻找高质量的解。以下是这些启发式算法的关系和主要特点：

1）MIP Heuristics（MIP启发式算法）：SCIP使用默认的混合整数规划（MIP）启发式算法，这些算法旨在从线性松弛问题的最优解或现有解出发，寻找好的整数和线性可行解。如果幸运的话，这些解也可能满足非线性约束。否则，它们提供了NLP局部搜索启发式算法的参考点。

2）NLP Local Search（NLP局部搜索启发式算法）：NLP局部搜索启发式算法专注于连续变量空间，通过将所有整数变量固定到参考点的值（例如，LP松弛问题的整数可行解），再寻找MINLP问题的一个局部最优解。每个可行解都是MINLP问题的可行解。SCIP可以切换不同的NLP求解器，具体选择取决于问题的性质。目前，SCIP仅使用内点法求解器IPOPT。

3）Undercover Heuristic（Undercover启发式算法）：Undercover启发式算法基于这样一个观察，即通常只需要固定一小部分变量，使得子问题中的所有约束都是线性的。这个子MIP问题更容易求解，并且其解立即满足原始MINLP问题的约束。选择要固定的变量是通过解一个集合覆盖问题来确定的，该问题的目标是最小化要固定的变量数量。固定变量的值来自LP或NLP松弛问题的解或已知的MINLP可行解。

4）Sub-MINLP Heuristics（子MINLP启发式算法）：子MINLP启发式算法的思想是将搜索范围限制在有望的、通常是接近最优或几乎可行的解的领域内。这个受启发式算法限制的问题通过固定变量或引入额外的约束来获得，从而使搜索更容易，并希望仍然能够找到高质量的解。SCIP的Sub-MINLP启发式算法是通过扩展用于MIP松弛问题的大邻域搜索（LNS）算法来实现的。LNS算法的关键特点是定义搜索领域的方式，这对于其成功至关重要。SCIP提供了多种LNS启发式算法，包括RINS、RENS、Crossover、Local Branching、DINS等，它们在搜索领域的定义和搜索策略上有所不同，以适应不同类型的问题。

综上所述，这些启发式算法在MINLP问题的求解中具有不同的功能和特点，它们旨在通过不同的策略来改善解的质量，并帮助SCIP有效地搜索解空间。根据问题的性质和求解状态，SCIP选择适当的启发式算法来寻找最佳解。这些算法的组合和切换可以提高求解器的性能。

04 总结

两篇文章结合起来，清楚地解释了SCIP是如何解决MINLP问题的。

欢迎大家订阅“量子计算HiQ”，查看更多论文分享和学术活动信息