量子计算论文精讲 | 黑盒优化算法：交叉熵QUBO和高阶因子分解机

已于 2024-03-24 20:20:31 修改
阅读量1.1k 收藏 9
点赞数 23
文章标签： 量子计算 算法
于 2024-03-24 19:50:56 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2401_83053014/article/details/136993546
版权

点击查看原文

图片

图片

欢迎大家扫码关注MindSpore Quantum Gitee社区

目录

内容简介

01 因子分解机+量子退火（FMQA）

02 基于交叉熵的BOX-QUBO算法

03  效果测试

- MAX-SAT

- Feedback Vertex Set (FVS)

- MaxClique

04 高阶因子分解机

05 总结

内容简介

黑盒优化指的是一些没有具体数学表达的优化问题，一种解决方案是引入代理模型去近似目标黑盒函数。通常假定代理模型是一个二阶或高阶交叉特征模型（形式与QUBO、HUBO相同）则可以使用量子算法求解。因子分解机(FMs)是一种监督学习方法，可以用于代理模型中特征系数的训练。本文将介绍利用交叉熵改进的因子分解机量子退火算法，以及高阶因子分解机对黑盒优化算法的可能改进。

相关论文1

标题：Black box optimization using QUBO and the cross entropy method
作者：Jonas N¨ußlein, Christoph Roch, Thomas Gabor, Jonas Stein, Claudia Linnhoff-Popien, and Sebastian Feld
期刊: Springer Nature Switzerland, 2023: 48-55

相关论文2

标题：Higher-Order Factorization Machines
作者：Mathieu Blondel, Akinori Fujino, Naonori Ueda, Masakazu Ishihata
会议: Advances in Neural Information Processing Systems, 2016, 29

01 因子分解机+量子退火（FMQA）

二阶交叉特征模型定义为

图片

待训练的是参数 ，每个 都是独立变量。在处理稀疏矩阵时由于交叉项太少，参数训练容易不充分。如果借助矩阵分解的思路将 看成是两个矩阵的乘积，重构特征系数后独立变量变少就可以达到用较少的数据得到特征矩阵的目的

图片

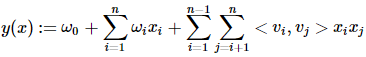
其中

图片

 是一个n维向量;  , 是低维向量（k维），V是由 组成的矩阵，  为两个k维向量的内积：

图片

k是一个超参。根据线性代数，对于任意对称正半定矩阵W，只要k足够大，一定存在矩阵V使得

图片

。对于黑盒问题，往往是我们预先设定代理模型为QUBO问题的形式，然后借助因子分解机训练得到交叉项的信息。当我们的模型重写为上式之后，每个  都是两个向量的内积因此一定是对称的，此外只要对角元素足够大，就能保证W是半正定的。

对于交叉项可以做一些变换简化计算

图片

原项求解的就是矩阵上三角之和，上式第1步就是整个矩阵之和减去矩阵的迹，然后求一半。经过这样的推导之后二阶FM最终表达为：

图片

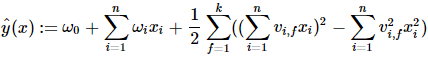
由此可以推导出FM对参数的梯度公式

图片

有了梯度公式，就可以用各种基于梯度的算法来训练模型了，FMQA算法流程为：

  1. 随机初始化若干个解作为初始训练集

  2. FM训练得到初始QUBO模型

  3. 在当前的QUBO模型（代理模型）下计算得到最优解

  4. 计算黑盒模型的损失函数

  5. 将新的解加入训练集并且重新训练更新QUBO模型

重复循环3-5步直到结束。

02 基于交叉熵的BOX-QUBO算法

交叉熵模型：交叉熵方法是一种通用的迭代优化方法。基本思想是给

最低0.47元/天 解锁文章
量子小Q
关注
神经网络在量子计算领域的应用:量子优化的AI先锋
AI天才研究院
05-05 423
1. 背景介绍 随着信息时代的迅猛发展，计算能力的需求呈指数级增长。传统的计算架构面临着摩尔定律的瓶颈，难以满足日益复杂的计算任务。量子计算作为一种颠覆性的计算范式，具有并行计算和指数加速的潜力，为解决传统计算难题带来了新的希望。 神经网络作为人工智能领域的核心技术之一，在图像识别、自然语言处理、机器翻译等领域取得了显著的成果。然而，神
最前沿・量子退火建模方法(1) : subQUBO讲解和python实现
gangshen1993的博客
04-13 4127
subQUBO思路和python实现。
LocalSolver快速入门指南（连载三十七) --Black-Box Optimization黑盒优化(概述)
qq_31243247的博客
03-12 1802
谨慎！ 如果该函数的计算成本不高并且可以在求解过程中进行数千次评估，那么使用黑盒函数可能不是最佳选择。考虑使用LocalSolver的外部函数. 注意： 请注意，此功能在 LSP 语言中不可用 注意： 此功能当前不支持集合变量。在本节中，我们将详细介绍如何在 LocalSolver 支持的每种编程语言（C++、Java、.NET、Python）中优化黑盒函数。为了说明这个描述，我们将通过一个黑盒界面来最小化 Branin 函数。演示目的，评估次数将限制在 20 次。 Branin函数的定义
black-box优化——第一篇：基础BBO算法
weixin_43509834的博客
06-04 3514
两个缩写： derivative free optimization (DFO) ：无导数优化 black-box optimization (BBO) ：黑箱优化 一、基本DFO算法 先介绍一些 naive 的方法来解决 BBO 问题，这样可以让大家了解到为什么DFO在实际中，如此受到欢迎。 1. ES算法（Exhaustive Search） 优化问题： min{f(x),x∈Ω} \begin{aligned} min\{f(x),x\in \Omega\} \end{aligned} min{f(x
Black Box Optimization学习笔记
weixin_44912626的博客
08-19 659
本页面解释了黑箱成本函数优化的进化策略的实现。 在这种情况下，黑盒意味着不能对代价函数做任何假设，例如，我们不能得到它的导数，我们甚至不知道它是否是连续的。 已经实现的进化策略都是基于**奖励加权平均(又名概率加权平均)**的，正如本文/演示中所解释的:http://icml.cc/discuss/2012/171.html 这里有一个1页的算法描述: http://www.pyoudeyer.com/stulpOudeyerDevelopmentalScience17.pdf#page=30 基本算法如下
Derivative-Free and Blackbox Optimization
11-24
这是关于黑盒优化的电子书，高清，最新版本，经典著作，英文版
一步步学习黑盒优化算法，借助达摩院MindOpt的RABBO榜单【系列1/4】
wuyoy520 的博客
12-22 3763
这次达摩院MindOpt优化求解器团队出的「开发者福利」黑盒优化RABBO V1.0看起来挺有意思的，什么是黑盒优化呢？怎么借助这个榜单学习这个技术呢？
量子计算论文精讲《量子退火启发算法在粒子轨迹重建中的应用》
最新发布
2401_83053014的博客
12-31 667
在预处理中，会对所有相邻的hits进行生成triplet的尝试，同时会对所生成triplet的质量进行评估，筛除掉明显不合理的连线。如图1所示，对撞机中的高速粒子在运动过程中会在一系列的探测器（黑线）上留下hits信号（绿点），而如何把这些离散的hits用曲线连接起来形成完整的轨迹即是轨迹重构需要解决的问题。目前主流的解决方案是卡尔曼滤波算法，它通过结合预测模型和实际观测值，递归地提供对系统状态的最佳估计，从而有效地减少测量误差并平滑轨迹，从一系列含有噪声的测量数据中估计出物体的真实轨迹。
AdiaQC:用于 Ising 自旋玻璃或 QUBO 问题的绝热量子计算求解器（包括几个测试问题）
06-16
绝热量子计算求解器用于模拟各种问题（包括一些机器学习问题）。 这是用 Python 2.7.4 编写的，仅在 Linux 上进行了测试，但可能对您有用（如果确实如此，请告诉我）。 需要 SciPy（NumPy、PyLab）。 可能通过一些...
黑盒算法识别-设计
KD的疯狂实验室
12-03 3163
start:2016年11月8日星期二 22:49 时间相关 硬件相关？ 是否循环？ 一一对应？ 有损？ 无损？ 空间映射变大？ 空间映射变小？ Hash？ 加密？ 哈希格式解读用途数据经过黑盒处理后变成另一种数据，它的过程总是有着各种魔力吸引你迫使你去搞清楚。往往我们不便于直接打开黑盒，直接用我们的大脑苦思冥想得到答案的机率想必不高。我也曾遭遇过这样的问题，并尝试用现有工具去
Python-blackbox一个用于并行优化黑盒子函数的Python模块
08-10
blackbox: 一个用于并行优化黑盒子函数的Python模块
pyqubo:用于从数学表达式构造QUBO的Python DSL
05-15
皮库伯 PyQUBO允许您根据灵活的数学表达式轻松创建QUBO或Ising模型。 PyQUBO的一些功能是 基于Python（C ++后端）。 与Ocean SDK完全集成。 （） 自动验证约束。 （ ） 用于参数调整的占位符。 （ ） 有关更多详细信息，请参见。 用法示例 创建QUBO 本示例构造一个简单的表达式并将其编译为model 。 通过调用model.to_qubo() ，我们得到结果QUBO。 （此示例解决了集合S = {4，2，7，1}的） >>> from pyqubo import Spin >>> s1, s2, s3, s4 = Spin( " s1 " ), Spin( " s2 " ), Spin( " s3 " ), Spin( " s4 " ) >>> H = ( 4 * s1 + 2 * s2 + 7 * s3 + s4) ** 2 >>> mo
（算法练习）——黑盒测试
晴空
01-06 339
黑盒测试统一在一篇博客里，不再区分。 要求：A+B 输入输出练习I http://codeup.cn/problem.php?cid=100000574&pid=0 说明： 感觉c[1000]用来暂存a+b的和就是耍流氓。。。但暂时还不会弄可变数组。。 代码： #include <stdio.h> #include <string.h> int main(){ i...
探索未知领域的优化利器：blackbox
gitblog_00481的博客
08-30 863
探索未知领域的优化利器：blackbox blackboxA Python module for parallel optimization of expensive black-box functions项目地址:https://gitcode.com/gh_mirrors/blac/blackbox 在当今的科研和技术实践中，优化问题无处不在，尤其是在面对那些计算成本高昂的“黑盒”函数时——...
“黑盒优化”是什么？
Drug discovery
11-03 1868
是一种优化技术，用于处理那些我们无法直接访问或理解其内部工作原理的系统或函数。在这种情况下，我们将该系统或函数视为一个“黑盒”，因为。【不利用导数信息】：与传统的基于导数的优化方法（例如梯度下降）不同，黑盒优化不需要函数的导数信息。：对于那些复杂的、不透明的、或者是不易于分析的系统，黑盒优化特别有用。：用户只需提供一个函数或评估标准，优化算法会尝试找到最佳的输入，以最大化或最小化输出。：由于缺乏内部信息，黑盒优化通常依赖于启发式搜索方法，如遗传算法、蒙特卡洛树搜索、贝叶斯优化等。
学习黑盒优化算法CMA和RandomSearch，借助阿里达摩院MindOpt的RABBO榜单【系列2/4】
wuyoy520 的博客
01-05 1916
这次达摩院MindOpt优化求解器团队出的「开发者福利」黑盒优化RABBO V1.0看起来挺有意思的，什么是黑盒优化呢？怎么借助这个榜单学习这个技术呢？RABBO内有内置CMA（CMA-ES, 协方差矩阵自适应进化策略)和Random Search（随机搜索），让我们来学一学~~
论文解读：Black-Box Tuning for Language-Model-as-a-Service
Mr_DreamQ的博客
11-07 1369
黑盒PLM调优
算法笔记重点(5)黑盒测试
BakenJ的博客
06-27 271
单点测试:PAT为典型例子，每一道题有若干次测试，每次测试都有相应的分数，所以正常情况下我们的程序执行一次即可，对输入输出要求相对较低。 多点测试:codeup等多数OJ为典型例子，我们需要一次满足多对输入，并且每次输入需要返回相应的输出，所有输出正确才能得分，否则为0分。 多点测试分为三类 1.while…EOF型 这种输入一般没有明确的结束条件，这要求在文件末尾前一直输入。我们需要用到scanf()的返回值，即在读取失败时返回的EOF(-1)。常见的代码结构是while(scanf(…)!=EOF){}
二次无约束二值优化模型（The Quadratic Unconstrained Binary Optimization(QUBO) model）
热门推荐
李宏宗的博客
08-28 1万+
（参考文献：Quantum Bridge Analytics I: a tutorial on formulating and using QUBO models） 一般形式 The Quadratic Unconstrained Binary Optimization model (QUBO) 根据二元的特性，可以将线性部分转化为二次部分 The linear part can be transformed into the quadratic part by this equation 对于有约束的
量子SDK原型开发：从QUBO到Ising转换的实现
资源摘要信息:"qsdk：Quantum SDK原型" 标题中提及的"Quantum SDK原型"暗示了一个旨在...此原型的开发表明了在量子计算领域内，为开发者提供一个方便的平台和工具，以探索量子算法和量子优化问题的解决途径的重要性。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值