谢启鸿高等代数第四版习题7.7部分习题解析part2.以及部分第7章复习题

本文链接：https://blog.csdn.net/2401_83247845/article/details/137412181

7.7部分

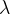定理：以 $\lambda$ 为特征值的K阶若当块个数为 $r(A-\lambda I_{n})^{k-1}+r(A-\lambda I_{n})^{k+1}-2r(A-\lambda I_{n})^{k}$

11.设n阶矩阵A的特征值全为1，求证：对任意的正整数K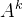， $A^{k}$ 与A相似。

证明： $\because$ $A$ = $PJP^{-1}$

$\therefore$ $A^{m}=PJ^{m}P^{-1}$ (易证故此处不再证明）

而且 $A^{m}$ 的特征值全为1。

$A^{m}$ 的特征值为1的k阶若当块的个数为

接下来只需证明 $J$ 相似于 $J^{m}$ 即可；

即证明两者有相同的约当标准型.

由书上7.8节的数学归纳可以知道，

$J^{m}=\begin{pmatrix} \lambda ^{k} & C^{1}_{m} \lambda ^{k-1}& ......&......\\ & ......& ......&......\\ & & \lambda ^{k} & C^{1}_{m}\lambda ^{k-1}\\ & & & \lambda ^{k} \end{pmatrix}$

$\therefore$ $J^{m}-\lambda ^{m}I_{n}=\begin{pmatrix} 0 & C^{1}_{m} \lambda ^{k-1}& ......&......\\ & ......& ......&......\\ & & 0 & C^{1}_{m}\lambda ^{k-1}\\ & & & 0 \end{pmatrix}$

$\therefore r(J^{m}-\lambda ^{m}I_{n})=r(J-\lambda I_{n})$

所以两者不仅特征值相同，相同特征值的K阶若当块个数也相同（运用上述定理即可得到）

所以两者相似。

12.设n阶矩阵A的特征值全为1或-1，求证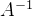： $A^{-1}$ 与A相似。

（本题的题干按照“特征值是1或者-1”理解）

证明： $\because$ $A$ = $PJP^{-1}$

$\therefore$ $A^{-1}=PJ^{-1}P^{-1}$

A的全部特征值为 $\left \{ \left. 1......1,-1......-1 \right \} \right.$ (设1有r个，-1有n-r个）

由 $A\eta =\lambda \eta$ 得到 $A^{-1}\eta =\lambda^{-1} \eta$ ，两者的特征值完全相同。

易知 $A$ 和 $A^{-1}$ 的若当标准型中只有主对角元为1和-1的若当块。

如果两者针对于同一特征值的的K阶若当块个数完全相同，两者的若当标准型相同，两者就相似了，所以下证两者同一特征值的的K阶若当块个数相同

而主对角元为1的K阶若当块个数为

$r(A-I_{n})^{k-1}+r(A-I_{n})^{k+1}-2r(A-I_{n})^{k}$

因为 $A-I_{n}=A(I_{n}-A^{-1})=(I_{n}-A^{-1})A$

所以对于任意的 $k\in N$ ,都有 $(A-I_{n})^{k}=(A(I_{n}-A^{-1}))^{k}=((I_{n}-A^{-1})A)^{k}$

$r((A-I_{n})^{k})=r((A(I_{n}-A^{-1}))^{k})=r(((I_{n}-A^{-1})A)^{k})$

A的特征值全都不为零，所以A是一个满秩矩阵。

所以 $r[(A-I_{n})^{k-1}]+r[(A-I_{n})^{k+1}]-2r[(A-I_{n})^{k}]=$

$r[(I_{n}-A^{-1})^{k-1}]+r[(I_{n}-A^{-1}]^{k+1})-2r[(I_{n}-A^{-1})^{k})]$

而负号不影响矩阵的秩，则A与A的逆矩阵关于特征值1的若当块个数相同（同理可以推出来当特征值-1时也成立）所以 $A^{-1}$ 与 $A$ 有相同的约当标准型。

所以两者相似。

复习题部分

3.设A是数域K上的n阶方阵，求证：A的极小多项式的次数小于等于r(A)+1.

易知存在可逆矩阵P，使得

$PAP^{-1}=\begin{pmatrix} c(d_{1(x)}) & & & \\ & c(d_{2(x)})& & \\ & & ......& \\ & & & c(d_{k(x)}) \end{pmatrix}$

其中 $d_{k}(x)=m_{A}(x)$

由相似矩阵有相同的秩可以得出

$r(A)=r(B)=\sum_{i=1}^{k}r(c(d_{k}(x)))\geqslant r(c(d_{k}(x)))\geqslant degd_{k}(x)-1=degm_{A}(x)-1$

将 $d_{k}(x)$ 看作一个多项式，根据他的友阵的性质可得到 $r(c(d_{k}(x)))\geqslant degd_{k}(x)-1$ （后一篇文章会详细总结友矩阵的全部内容。）

4.设A是数域K上的n阶矩阵，求证：若tr(A)=0,则A相似于一个K上的主对角元全为零的矩阵。

本题采用数学归纳法。

当n=1时，若tr(A)=0，A=0。

下面假设n-1时成立，当n时，A的有理标准型

$B=\begin{pmatrix} c(d_{1}(x))& & \\ & ......& \\ & &c(d_{k(x)}) \end{pmatrix}$ 【A相似于B，所以只要证明B相似于一个K上的主对角元全为零的矩阵即可】

(1)若 $degd_{k}(x)=1$ ,即 $d_{k}(x)=x-c$ ,此时 $d_{1}(x)=......=d_{k}(x)=x-c$ ,且k=n.

$B=cI_{n}$ ,从而

tr(A)=tr(B)=n·c=0,所以c=0.

B为零矩阵，结论一定成立。

(2）若 $dead_{k}(x)>1$ ,则有一个有理块，是多阶友阵的形式，左上角为0，把这个有理块挪到最上面，则会得到B的（1，1）元素为0

不妨设

$B=\begin{pmatrix} 0& \beta ^{'}\\ \alpha & B_{1} \end{pmatrix}$ 由于tr(A)=tr(B)=tr(B1)=0;

（B1是n-1阶的）

由归纳假设【（n-1）阶】存在Q，使得 $Q^{-1}B_{1}Q$ 的主对角线为0

令 $P=\begin{pmatrix} 1& 0\\ 0& Q \end{pmatrix}$ ，则有

$P^{-1}BP=\begin{pmatrix} 0& x\\ x& Q^{-1}BQ \end{pmatrix}$

$\begin{pmatrix} 0& x\\ x& Q^{-1}BQ \end{pmatrix}$ 这个矩阵是主对角线全为零的。所以A相似于一个K上的主对角元全为零的矩阵。

谢启鸿高等代数第四版习题7.7部分习题解析part2.以及部分第7章复习题

7.7部分

定理：以 $\lambda$ 为特征值的K阶若当块个数为 $r(A-\lambda I_{n})^{k-1}+r(A-\lambda I_{n})^{k+1}-2r(A-\lambda I_{n})^{k}$

11.设n阶矩阵A的特征值全为1，求证：对任意的正整数K， $A^{k}$ 与A相似。

12.设n阶矩阵A的特征值全为1或-1，求证： $A^{-1}$ 与A相似。

复习题部分

3.设A是数域K上的n阶方阵，求证：A的极小多项式的次数小于等于r(A)+1.

4.设A是数域K上的n阶矩阵，求证：若tr(A)=0,则A相似于一个K上的主对角元全为零的矩阵。

结语：有用请点赞，有错误欢迎指出！等会还会有复习题部分哦！

（好困，想睡觉。）

谢启鸿高等代数第四版习题7.7部分习题解析part2.以及部分第7章复习题

7.7部分

定理：以为特征值的K阶若当块个数为

11.设n阶矩阵A的特征值全为1，求证：对任意的正整数K，与A相似。

12.设n阶矩阵A的特征值全为1或-1，求证：与A相似。

复习题部分

3.设A是数域K上的n阶方阵，求证：A的极小多项式的次数小于等于r(A)+1.

4.设A是数域K上的n阶矩阵，求证：若tr(A)=0,则A相似于一个K上的主对角元全为零的矩阵。

结语：有用请点赞，有错误欢迎指出！等会还会有复习题部分哦！

（好困，想睡觉。）

定理：以 $\lambda$ 为特征值的K阶若当块个数为 $r(A-\lambda I_{n})^{k-1}+r(A-\lambda I_{n})^{k+1}-2r(A-\lambda I_{n})^{k}$

11.设n阶矩阵A的特征值全为1，求证：对任意的正整数K， $A^{k}$ 与A相似。

12.设n阶矩阵A的特征值全为1或-1，求证： $A^{-1}$ 与A相似。