最后的话
最近很多小伙伴找我要Linux学习资料,于是我翻箱倒柜,整理了一些优质资源,涵盖视频、电子书、PPT等共享给大家!
资料预览
给大家整理的视频资料:

给大家整理的电子书资料:

如果本文对你有帮助,欢迎点赞、收藏、转发给朋友,让我有持续创作的动力!
网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!
定义基础模型
dt = DecisionTreeClassifier()
#创建装袋集成
bag = BaggingClassifier(base_estimator=dt, n_estimators= 10 )
在数据上拟合
集成 bag.fit(X, y)
进行预测
y_pred = bag.predict(X)
评估性能
acc = precision_score(y, y_pred )
acc = acc * 100
print ( f’准确度: {acc: .2 f} %’ )
### 3.5 提升

组合多个模型的最后一种方法是以顺序和迭代的方式使用它们。例如,如果你有一个模型预测巴黎的温度为15°C,你可以使用其误差或残差作为另一个模型的输入,该模型试图纠正这些误差并做出更好的预测。你可以多次重复这个过程,得到相互从彼此错误中学习的不同模型。这也被称为自适应提升或AdaBoost。
提升的优点在于它降低了预测的方差和偏差,意味着它们更有可能接近并准确地反映真实值。缺点在于它可能对异常值和噪声更为敏感,意味着它可能对数据过拟合或欠拟合。
要在Python中使用scikit-learn实现提升集成,对于回归问题,我们可以使用AdaBoostRegressor类,对于分类问题,我们可以使用AdaBoostClassifier类。这些类允许我们指定一个基本估算器和提升迭代的次数。
以下是如何在回归问题中使用提升集成的示例:
导入库
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn.datasets import load_iris
from sklearn.metrics importmean_squared_error #
加载数据
X, y = load_iris(return_X_y= True )
定义基础模型
dt = DecisionTreeRegressor()
#创建增强集成
boost = AdaBoostRegressor(base_estimator=dt, n_estimators= 10 )
根据数据拟合集成
boost.fit(X, y)
进行预测
y_pred = boost.predict(X)
评估性能
mse = Mean_squared_error(y, y_pred)
打印(f’MSE:{mse:.2 f} ')
## 4. 分析预测模型的泛化误差
从模型角度看:
* **Bias**(偏置):衡量一个分类器进行错误预测的趋势。
* **Variance**(变异度):衡量一个分类器预测结果的偏离程度。
如果一个模型有更小的Bias和Variance 就代表这个模型的泛化性能很好。
## 5. 几何直观地理解集成学习的四大类型
### 5.1 装袋法 Bagging(实例操作)
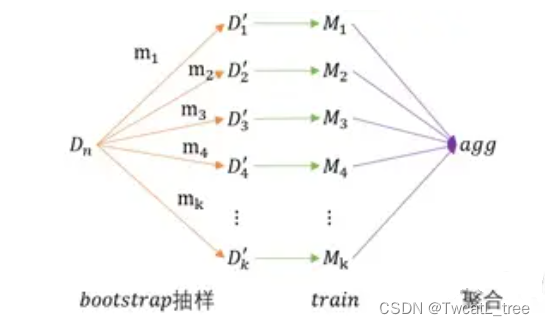
1. 将大小为
n
n
n 的原始数据
D
n
D\_n
Dn ,进行Bootstrap抽样(有放回抽样),因此在各抽样数据集
D
i
′
D\_i'
Di′ 中,存在部分元素重复;各抽样数据集的样本容量
m
i
≤
n
m\_i≤n
mi≤n
2. 将抽样后的数据集,分别独立进行模型学习
3. 然后将
k
k
k 个模型进行聚合;分类:多数投票;回归:平均数、中位数
>
> * 没有一个模型是在整个数据集上训练的
> * 如果原始数据集部分元素发生异常变化,可能会影响子模型,而不影响聚合后的模型,
> * 因此:“取偏差小 、方差大的基础模型,将其聚合,得到偏差小、方差小的模型”
>
>
>
**Bagging = bootstrap aggregating(自举汇聚法)**
装袋法思想源于数据越多,性能越好的直觉判断。
**具体方法:**
>
> 通过随机抽样与替换相结合的方式构建新的数据集 。
>
>
>
将原始数据集进行有放回的随机采样次,得到了个数据集,针对这些数据集一共产生个不同的基分类器。对于这个分类器,让他们采用投票法来决定最终的分类结果。
**例子:**
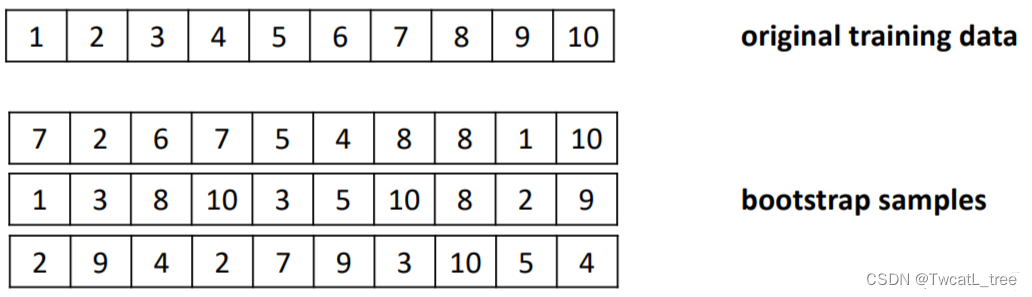
**袋装法存在的问题:**
因为袋装法是有放回的随机采样
N
N
N次,那就有可能有些样本可能永远不会被随机到。因为
N
N
N个样本,每个样本每次被取到的概率为
1
N
\frac{1}{N}
N1,那么一共取
N
N
N次没取到的概率为
(
1
−
1
N
)
N
\left ( 1-\frac{1}{N} \right )^{N}
(1−N1)N这个值在
N
N
N很大的时候的极限值
≈
0.37
\approx 0.37
≈0.37。
**装袋法的特点:**
* 始终使用相同的基分类算法。
* 减少预测的
V
a
r
i
a
n
c
e
Variance
Variance(通过接受一些
B
i
a
s
Bias
Bias)。
* 对不稳定的分类器(训练集的微小变化会导致预测的巨大变化)有效。
* 可能会使稳定分类器的性能略有下降。
* 基于抽样(构造基分类器的三种方法中的实例操作)和投票的简单方法。
* 多个单独的基分类器可以同步并行进行计算。
* 可以有效的克服数据集中的噪声数据,因为异常值可能会消失(
≈
0.63
\approx 0.63
≈0.63)。
* 性能通常比基分类器要好得多,只是偶尔会比基分类器差。
### 5.2 随机森林法 Random Forest(特征操作)
具有良好深度的决策树就是 低偏差 和 高方差 的模型;因此用决策树做基础模型的Bagging(装袋算法),也称**随机森林**
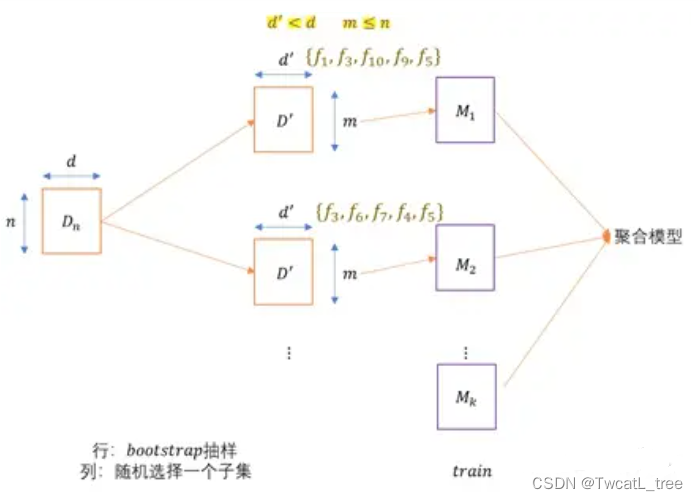
* 对于原始数据集的 行:进行Bootstrap抽样(有放回抽样),大小为 m 的样本容量
* 对于原始数据集的 列:随机选择一个特征子集
* 在每个行抽样的数据集中,剩下的数据点(也称袋外点)可以用于相应子模型的交叉验证(以了解每个基础学习者的性能)
1. 随着基础模型数量的增加 ,聚合的模型的方差减少
2. 偏差(单个模型) ≈ 偏差(聚合后)
3. 列采样率:
d
′
d
\frac{d'}{d}
dd′ ;行采样率:
m
n
\frac{m}{n}
nm ;如果这两个比值减小,基础模型方差也减小,因此聚合模型的方差也会减少,一般情况固定,不需要认为优化
4. 基础模型的个数 k ,为超参数,可以根据交叉验证进行确认最优
5. 特征重要性:对每个基础模型的特征的信息增益求和,再在各特征中进行比较,较大信息增益为较重要特征
>
> 随机森林法的基分类器是随机树:一棵决策树,但每个节点只考虑一些可能的属性。
>
>
>
可以通过下图回忆什么是决策树:
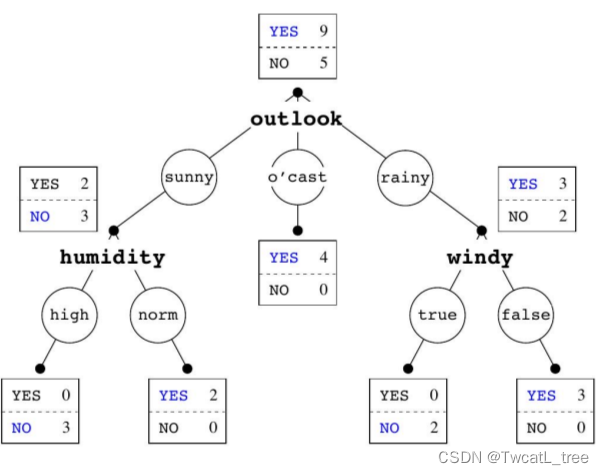
也就是说随机树使用的特征空间不是训练集全部的特征空间
* 例如,采用一个固定的比例来选择每个决策树的特征空间大小。
* 随机森林中的每棵树的建立都比一个单独的决策树要简单和快速;但是这种方法增加了模型的 。
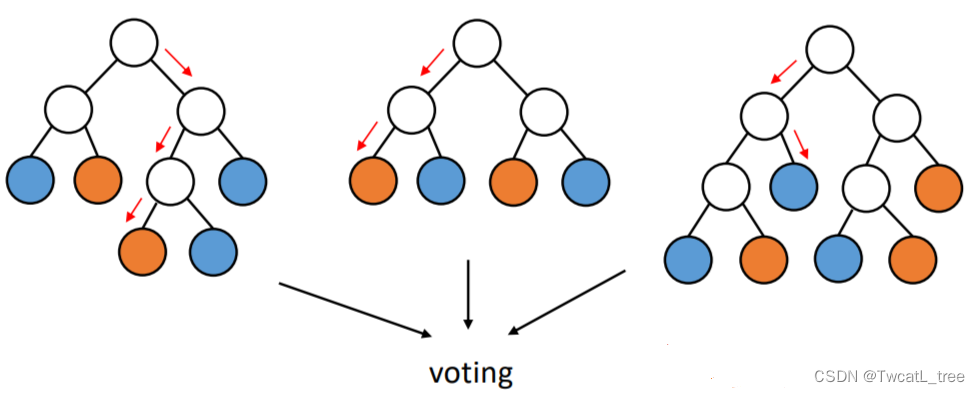
森林就是多个随机树的集合
* 每棵树都是用不同的袋装训练数据集建立的。
* 综合分类是通过投票进行的。
**随机森林的超参数:**
树的**数量B**,可以根据“out-of-bag”误差进行调整。
特征子**样本大小**:随着它的增加,分类器的强度和相关性都增加
(
⌊
l
o
g
2
∣
F
∣
+
1
⌋
)
\left ( \left \lfloor log\_{2}\left | F \right | + 1 \right \rfloor \right )
(⌊log2∣F∣+1⌋)。因为随机森林中的每棵树使用的特征越多,其与森林中其他树的特征重合度就可能越高,导致产生的随机数相似度越大。
**可解释性**:单个实例预测背后的逻辑可以通过多棵随机树共同决定。
**随机森林的特点**:
* 随机森林非常强大,可以高效地进行构建。
* 可以并行的进行。
* 对过拟合有很强的鲁棒性。
* 可解释性被牺牲了一部分,因为每个树的特征都是特征集合中随机选取的一部分。
### 5.3 演进法 Boosting(算法操作)
演进法的思想源于调整基础分类器,使其专注于难以分类的实例的直觉判断。
**具体方法:**
>
> 迭代地改变训练实例的分布和权重,以反映分类器在前一次迭代中的表现。
>
>
>
* 从初始训练集训练出一个基学习器;这时候每个样本的权重都为。
* 每个都会根据上一轮预测结果调整训练集样本的权重。
* 基于调整后的训练集训练一个新的基学习器。
* 重复进行,直到基学习器数量达到开始设置的值。
* 将个基学习器通过加权的投票方法(weighted voting)进行结合。
**例子:**

对于boosting方法,有两个问题需要解决:
* 每一轮学习应该如何改变数据的概率分布
* 如何将各个基分类器组合起来
**Boosting集成方法的特点:**
* 他的基分类器是决策树或者 OneR 方法。
* 数学过程复杂,但是计算的开销较小;整个过程建立在迭代的采样过程和加权的投票(voting)上。
* 通过迭代的方式不断的拟合残差信息,最终保证模型的精度。
* 比bagging方法的计算开销要大一些。
* 在实际的应用中,boosting的方法略有过拟合的倾向(但是不严重)。
* 可能是最佳的词分类器(gradient boosting)。
#### 5.3.1 演进法实例:AdaBoost
Adaptive Boosting(自适应增强算法):是一种顺序的集成方法(随机森林和 Bagging 都属于并行的集成算法)。
具体方法:
有T个基分类器:
C
1
,
C
2
,
.
.
.
,
C
i
,
.
.
,
C
T
C\_{1},C\_{2},...,C\_{i},..,C\_{T}
C1,C2,...,Ci,..,CT。
训练集表示为
{
x
i
,
y
j
∣
j
=
1
,
2
,
.
.
.
,
N
}
\left \{ x\_{i},y\_{j}|j=1,2,...,N \right \}
{xi,yj∣j=1,2,...,N}。
初始化每个样本的权重都为
1
N
\frac{1}{N}
N1,即:
{
w
j
(
1
)
=
1
N
∣
j
=
1
,
2
,
.
.
.
,
N
}
\left \{ w\_{j}^{(1)=\frac{1}{N}}|j=1,2,...,N \right \}
{wj(1)=N1∣j=1,2,...,N}。
在每个iteration i 中,都按照下面的步骤进行:
>
> 计算错误率 error rate
>
>
>
>
>
>
>
>
> ξ
>
>
> i
>
>
>
> =
>
>
>
> ∑
>
>
>
> j
>
>
> =
>
>
> 1
>
>
>
> N
>
>
>
>
> w
>
>
> j
>
>
>
> (
>
>
> i
>
>
> )
>
>
>
>
> δ
>
>
> (
>
>
>
> C
>
>
> j
>
>
>
> (
>
>
>
> x
>
>
> j
>
>
>
> )
>
>
> ≠
>
>
>
> y
>
>
> j
>
>
>
> )
>
>
>
> \xi \_{i}=\sum \_{j=1}^{N} w\_{j}^{(i)}\delta (C\_{j}(x\_{j})\neq y\_{j})
>
>
> ξi=∑j=1Nwj(i)δ(Cj(xj)=yj)
>
>
>
>
>
>
>
> δ
>
>
>
> (
>
>
> )
>
>
>
>
> \delta \left ( \right)
>
>
> δ()是一个indicator函数,当函数的条件满足的时候函数值为1;即,当弱分类器
>
>
>
>
>
> C
>
>
> i
>
>
>
>
> C\_{i}
>
>
> Ci对样本
>
>
>
>
>
> x
>
>
> j
>
>
>
>
> x\_{j}
>
>
> xj进行分类的时候如果分错了就会累积
>
>
>
>
>
> w
>
>
> j
>
>
>
>
> w\_{j}
>
>
> wj。
>
>
>
>
> 使用
>
>
>
>
>
> ξ
>
>
> i
>
>
>
>
> \xi \_{i}
>
>
> ξi来计算每个基分类器
>
>
>
>
>
> C
>
>
> i
>
>
>
>
> C\_{i}
>
>
> Ci的重要程度(给这个基分类器分配权重
>
>
>
>
>
> α
>
>
> i
>
>
>
>
> \alpha \_{i}
>
>
> αi)
>
>
>
>
>
>
>
>
> α
>
>
> i
>
>
>
> =
>
>
>
> 1
>
>
> 2
>
>
>
> l
>
>
> n
>
>
>
>
> 1
>
>
> −
>
>
>
> ε
>
>
> i
>
>
>
>
>
> ε
>
>
> i
>
>
>
>
>
> \alpha \_{i}=\frac{1}{2}ln\frac{1-\varepsilon \_{i}}{\varepsilon \_{i}}
>
>
> αi=21lnεi1−εi
>
>
> 从这个公式也能看出来,当
>
>
>
>
>
> C
>
>
> i
>
>
>
>
> C\_{i}
>
>
> Ci 判断错的样本量越多,得到的
>
>
>
>
>
> ξ
>
>
> i
>
>
>
>
> \xi \_{i}
>
>
> ξi就越大,相应的
>
>
>
>
>
> α
>
>
> i
>
>
>
>
> \alpha \_{i}
>
>
> αi就越小(越接近0)
>
>
> 根据
>
>
>
>
>
> α
>
>
> i
>
>
>
>
> \alpha \_{i}
>
>
> αi来更新每一个样本的权重参数,为了第i+1个iteration做准备:
>
>
>
>
>
>
>
>
> w
>
>
> j
>
>
>
> (
>
>
> i
>
>
> +
>
>
> 1
>
>
> )
>
>
>
>
> =
>
>
>
>
> w
>
>
> j
>
>
>
> (
>
>
> i
>
>
> )
>
>
>
>
>
> Z
>
>
>
> (
>
>
> i
>
>
> )
>
>
>
>
>
> ×
>
>
>
> {
>
>
>
>
>
>
>
> e
>
>
>
> −
>
>
>
> α
>
>
> i
>
>
>
>
>
>
>
>
>
>
> i
>
>
> f
>
>
>
> C
>
>
> i
>
>
>
> (
>
>
>
> x
>
>
> j
>
>
>
> )
>
>
> =
>
>
>
> y
>
>
> j
>
>
>
>
>
>
>
>
>
>
>
> e
>
>
>
> α
>
>
> i
>
>
>
>
>
>
>
>
>
> i
>
>
> f
>
>
>
> C
>
>
> i
>
>
>
> (
>
>
>
> x
>
>
> j
>
>
>
> )
>
>
> ≠
>
>
>
> y
>
>
> j
>
>
>
>
>
>
>
>
>
>
> w\_{j}^{(i+1)}=\frac{w\_{j}^{(i)}}{Z^{(i)}}\times \left\{\begin{matrix} e^{-\alpha \_{i}} &ifC\_{i}(x\_{j})=y\_{j} \\ e^{\alpha \_{i}} & ifC\_{i}(x\_{j})\neq y\_{j} \end{matrix}\right.
>
>
> wj(i+1)=Z(i)wj(i)×{e−αieαiifCi(xj)=yjifCi(xj)=yj
>
>
> 样本j的权重由
>
>
>
>
>
> w
>
>
> j
>
>
>
> (
>
>
> i
>
>
> )
>
>
>
>
>
> w\_{j}^{(i)}
>
>
> wj(i)变成
>
>
>
>
>
> w
>
>
> j
>
>
>
> (
>
>
> i
>
>
> +
>
>
> 1
>
>
> )
>
>
>
>
>
> w\_{j}^{(i+1)}
>
>
> wj(i+1)这个过程中发生的事情是:如果这个样本在第i个iteration中被判断正确了,他的权重就会在原本KaTeX parse error: Expected '}', got 'EOF' at end of input: w\_{j}^{(i)}的基础上乘以
>
>
>
>
>
> e
>
>
>
> −
>
>
>
> α
>
>
> i
>
>
>
>
>
>
> e^{-\alpha \_{i}}
>
>
> e−αi;根据上面的知识
>
>
>
>
>
> α
>
>
> i
>
>
>
> >
>
>
> 0
>
>
>
> \alpha \_{i} > 0
>
>
> αi>0因此
>
>
>
>
> −
>
>
>
> α
>
>
> i
>
>
>
> <
>
>
> 0
>
>
>
> -\alpha \_{i} < 0
>
>
> −αi<0所以根据公式我们可以知道,那些被分类器预测错误的样本会有一个大的权重;而预测正确的样本则会有更小的权重。
>
>
>
>
>
>
>
>
> Z
>
>
>
> (
>
>
> i
>
>
> )
>
>
>
>
>
> Z^{(i)}
>
>
> Z(i)是一个normalization项,为了保证所有的权重相加之和为1。
>
>
>
>
> 最终将所有的
>
>
>
>
>
> C
>
>
> i
>
>
>
>
> C\_{i}
>
>
> Ci按照权重进行集成
>
>
>
>
> 持续完成从i=2,…,T的迭代过程,但是当
>
>
>
>
>
> ε
>
>
> i
>
>
>
> >
>
>
> 0.5
>
>
>
> \varepsilon\_{i} > 0.5
>
>
> εi>0.5的时候需要重新初始化样本的权重最终采用的集成模型进行分类的公式:
>
>
>
>
>
>
>
>
> C
>
>
> ∗
>
>
>
> (
>
>
> x
>
>
> )
>
>
> =
>
>
> a
>
>
> r
>
>
> g
>
>
> m
>
>
> a
>
>
>
> x
>
>
> y
>
>
>
>
> ∑
>
>
>
> i
>
>
> =
>
>
> 1
>
>
>
> T
>
>
>
>
> α
>
>
> i
>
>
>
> δ
>
>
> (
>
>
>
> C
>
>
> i
>
>
>
> (
>
>
> x
>
>
> )
>
>
> =
>
>
> y
>
>
> )
>
>
>
> C^{\*}(x)=argmax\_{y}\sum \_{i=1}^{T}\alpha \_{i}\delta (C\_{i}(x)=y)
>
>
> C∗(x)=argmaxy∑i=1Tαiδ(Ci(x)=y)
>
>
> 这个公式的意思大概是:例如我们现在已经得到了3个基分类器,他们的权重分别是0.3, 0.2, 0.1所以整个集成分类器可以表示为:
>
>
>
>
>
>
>
> C
>
>
> (
>
>
> x
>
>
> )
>
>
> =
>
>
>
> ∑
>
>
>
> i
>
>
> =
>
>
> 1
>
>
>
> T
>
>
>
>
> α
>
>
> i
>
>
>
>
> C
>
>
> i
>
>
>
> (
>
>
> x
>
>
> )
>
>
> =
>
>
> 0.3
>
>
>
> C
>
>
> 1
>
>
>
> (
>
>
> x
>
>
> )
>
>
> +
>
>
> 0.2
>
>
>
> C
>
>
> 2
>
>
>
> (
>
>
> x
>
>
> )
>
>
> +
>
>
> 0.1
>
>
>
> C
>
>
> 3
>
>
>
> (
>
>
> x
>
>
> )
>
>
>
> C(x)=\sum \_{i=1}^{T}\alpha \_{i}C\_{i}(x)=0.3C\_{1}(x)+0.2C\_{2}(x)+0.1C\_{3}(x)
>
>
> C(x)=∑i=1TαiCi(x)=0.3C1(x)+0.2C2(x)+0.1C3(x)
>
>
> 如果类别标签一共只有0, 1那就最终的C(x)对于0的值大还是对于1的值大了。
>
>
> 只要每一个基分类器都比随机预测的效果好,那么最终的集成模型就会收敛到一个强很多的模型。
>
>
>
#### 5.3.2 装袋法/随机森林和演进法对比
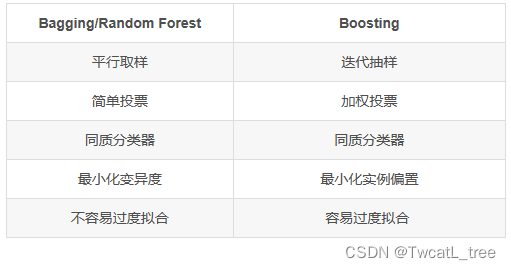
装袋法和演进法的对比:
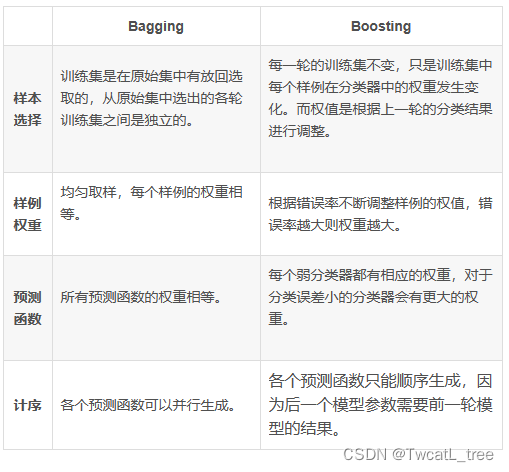
装袋法/随机森林 以及演进法对比
### 5.4 堆叠法 Stacking
堆叠法的思想源于在不同偏置的算法范围内平滑误差的直觉。
方法:采用多种算法,这些算法拥有不同的偏置
>
> 在基分类器(level-0 model) 的输出上训练一个元分类器(meta-classifier)也叫level-1 model
>
>
> 了解哪些分类器是可靠的,并组合基分类器的输出 使用交叉验证来减少偏置
>
>
>
>
> Level-0:基分类器
>
>
> 给定一个数据集 ( X , y ) 可以是SVM, Naive Bayes, DT等
>
>
>
>
> Level-1:集成分类器
>
>
> 在Level-0分类器的基础上构建新的attributes
> 每个Level-0分类器的预测输出都会加入作为新的attributes;如果有M个Level-0分离器最终就会加入M个attributes
> 删除或者保持原本的数据X 考虑其他可用的数据(NB概率分数,SVM权重) 训练meta-classifier来做最终的预测
>
>
>
可视化这个stacking过程:
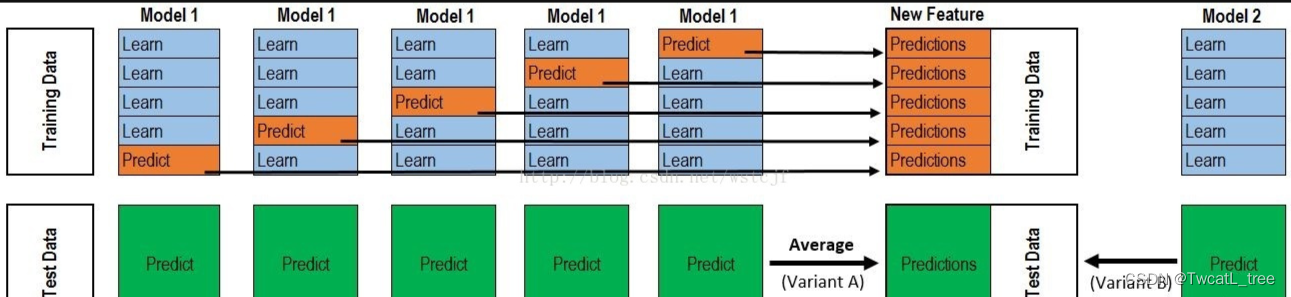
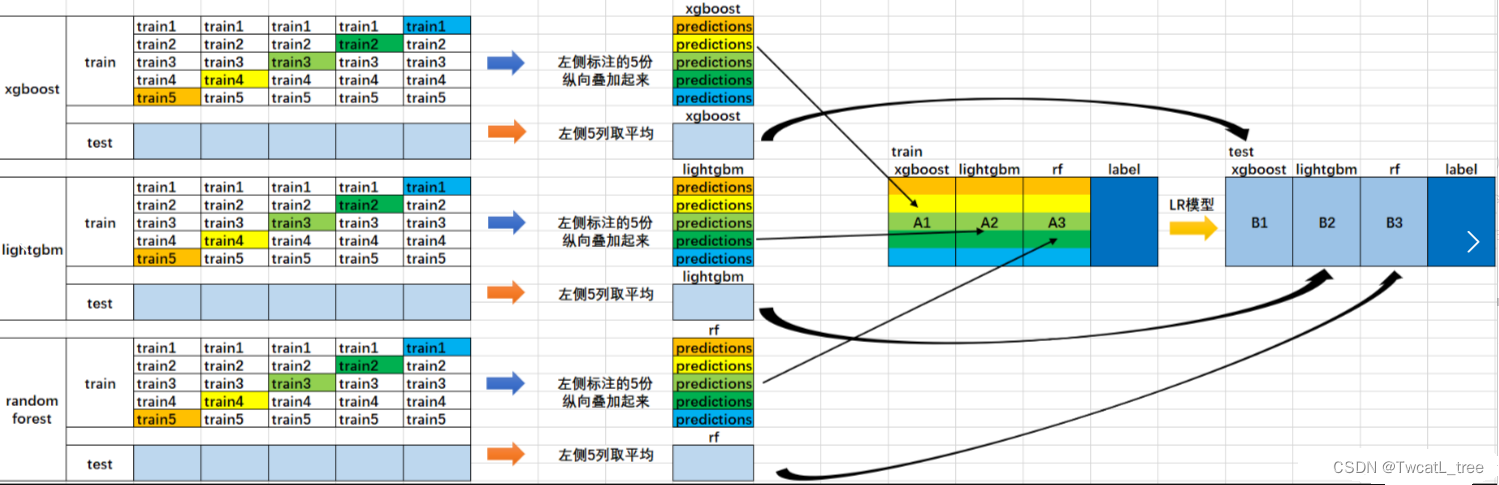
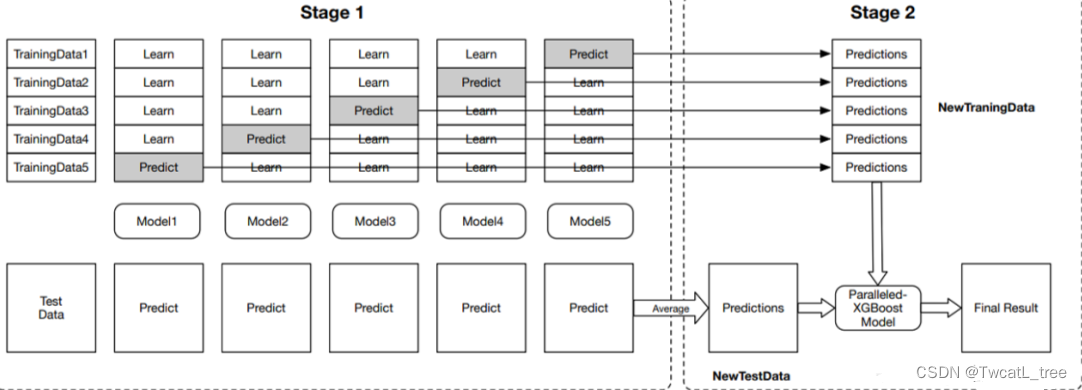
**stacking方法的特点:**
* 结合多种不同的分类器
* 数学表达简单,但是实际操作耗费计算资源
* 通常与基分类器相比,stacking的结果一般好于最好的基分类器
>
> ***PS:读到这里你大概已经了解集成学习了,如果你想更深入了解的话可以继续读下去***
>
>
>
## 6. 深入介绍集成技术
### 6.1 集成学习介绍
我们通过一个例子来理解集成学习的概念。假设你是一名电影导演,你依据一个非常重要且有趣的话题创作了一部短片。现在,你想在公开发布前获得影片的初步反馈(评级)。有哪些可行的方法呢?
**A:可以请一位朋友为电影打分。**
于是完全有可能出现这种结果:你所选择的人由于非常爱你,并且不希望给你这部糟糕的影片打1星评级来伤害你脆弱的小心脏。
**B:另一种方法是让你的5位同事评价这部电影。**
这个办法应该更好,可能会为电影提供更客观诚实的评分。但问题依然存在。这5个人可能不是电影主题方面的“专家”。当然,他们可能懂电影摄制,镜头或音效,但他们可能并不是黑色幽默的最佳评判者。
**C:让50个人评价这部电影呢?**
其中一些可以是你的朋友,可以是你的同事,甚至是完完全全的陌生人。
在这种情况下,回应将更加普遍化和多样化,因为他们拥有不同的技能。事实证明,与我们之前看到的情况相比,这是获得诚实评级的更好方法。
通过这些例子,你可以推断,与个人相比,不同群体的人可能会做出更好的决策。与单一模型相比,各种不同模型也是这个道理。机器学习中的多样化是通过称为集成学习(Ensemble learning)的技术实现的。
现在你已经掌握了集成学习的要旨,接下来让我们看看集成学习中的各种技术及其实现。
###
### 6.2 简单集成技术
这一节中,我们会看一些简单但是强大的技术,比如:
* **最大投票法**
* **平均法**
* **加权平均法**
###
#### 6.2.1 最大投票法
最大投票方法通常用于分类问题。这种技术中使用多个模型来预测每个数据点。每个模型的预测都被视为一次“投票”。大多数模型得到的预测被用作最终预测结果。
例如,当你让5位同事评价你的电影时(最高5分); 我们假设其中三位将它评为4,而另外两位给它一个5。由于多数人评分为4,所以最终评分为4。你可以将此视为采用了所有预测的众数(mode)。
最大投票的结果有点像这样:


**示例代码:**
这里x\_train由训练数据中的自变量组成,y\_train是训练数据的目标变量。验证集是x\_test(自变量)和y\_test(目标变量)。
>
> model1 = tree.DecisionTreeClassifier()
>
> model2 = KNeighborsClassifier()
>
> model3= LogisticRegression()
>
>
>
> model1.fit(x\_train,y\_train)
>
> model2.fit(x\_train,y\_train)
>
> model3.fit(x\_train,y\_train)
>
>
>
> pred1=model1.predict(x\_test)
>
> pred2=model2.predict(x\_test)
>
> pred3=model3.predict(x\_test)
>
>
>
> final\_pred = np.array([])
>
> for i in range(0,len(x\_test)):
>
> final\_pred =np.append(final\_pred, mode([pred1[i], pred2[i], pred3[i]]))
>
或者,你也可以在sklearn中使用“VotingClassifier”模块,如下所示:
>
> from sklearn.ensemble import VotingClassifier
>
> model1 = LogisticRegression(random\_state=1)
>
> model2 = tree.DecisionTreeClassifier(random\_state=1)
>
> model = VotingClassifier(estimators=[(‘lr’, model1), (‘dt’, model2)], voting=‘hard’)
>
> model.fit(x\_train,y\_train)
>
> model.score(x\_test,y\_test)
>
###
#### 6.2.2 平均法
类似于最大投票技术,这里对每个数据点的多次预测进行平均。在这种方法中,我们从所有模型中取平均值作为最终预测。平均法可用于在回归问题中进行预测或在计算分类问题的概率时使用。
例如,在下面的情况中,平均法将取所有值的平均值。
即(5 + 4 + 5 + 4 + 4)/ 5 = 4.4


**示例代码:**
>
> model1 = tree.DecisionTreeClassifier()
>
> model2 = KNeighborsClassifier()
>
> model3= LogisticRegression()
>
>
>
> model1.fit(x\_train,y\_train)
>
> model2.fit(x\_train,y\_train)
>
> model3.fit(x\_train,y\_train)
>
>
>
> pred1=model1.predict\_proba(x\_test)
>
> pred2=model2.predict\_proba(x\_test)
>
> pred3=model3.predict\_proba(x\_test)
>
>
>
> finalpred=(pred1+pred2+pred3)/3
>
### **2.3 加权平均法**
这是平均法的扩展。为所有模型分配不同的权重,定义每个模型的预测重要性。例如,如果你的两个同事是评论员,而其他人在这方面没有任何经验,那么与其他人相比,这两个朋友的答案就更加重要。
计算结果为[(5 \* 0.23)+(4 \* 0.23)+(5 \* 0.18)+(4 \* 0.18)+(4 \* 0.18)] = 4.41。

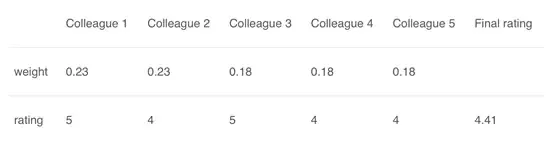
**示例代码:**
>
> model1 = tree.DecisionTreeClassifier()
>
> model2 = KNeighborsClassifier()
>
> model3= LogisticRegression()
>
>
>
> model1.fit(x\_train,y\_train)
>
> model2.fit(x\_train,y\_train)
>
> model3.fit(x\_train,y\_train)
>
>
>
> pred1=model1.predict\_proba(x\_test)
>
> pred2=model2.predict\_proba(x\_test)
>
> pred3=model3.predict\_proba(x\_test)
>
>
>
> finalpred=(pred1
> *0.3+pred2*0.3+pred3\*0.4)
>
###
### 6.3 高级集成技术
我们已经介绍了基础的集成技术,让我们继续了解高级的技术。
###
#### 6.3.1 堆叠(Stacking)
堆叠是一种集成学习技术,它使用多个模型(例如决策树,knn或svm)的预测来构建新模型。该新模型用于对测试集进行预测。以下是简单堆叠集成法的逐步解释:
**第一步:**把训练集分成10份


**第二步:**基础模型(假设是决策树)在其中9份上拟合,并对第10份进行预测。
**第三步:**对训练集上的每一份如此做一遍。


**第四步:**然后将基础模型(此处是决策树)拟合到整个训练集上。
**第五步:**使用此模型,在测试集上进行预测。
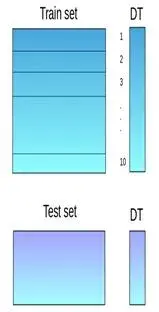
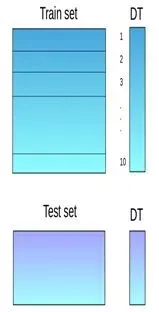
**第六步:**对另一个基本模型(比如knn)重复步骤2到4,产生对训练集和测试集的另一组预测。


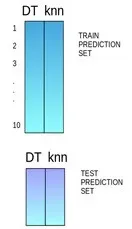
**第七步:**训练集预测被用作构建新模型的特征。
**第八步:**该新模型用于对测试预测集(test prediction set,上图的右下角)进行最终预测。

**示例代码:**
我们首先定义一个函数来对n折的训练集和测试集进行预测。此函数返回每个模型对训练集和测试集的预测。
>
> def Stacking(model,train,y,test,n\_fold):
>
> folds=StratifiedKFold(n\_splits=n\_fold,random\_state=1)
>
> test\_pred=np.empty((test.shape[0],1),float)
>
> train\_pred=np.empty((0,1),float)
>
> for train\_indices,val\_indices in folds.split(train,y.values):
>
> x\_train,x\_val=train.iloc[train\_indices],train.iloc[val\_indices]
>
> y\_train,y\_val=y.iloc[train\_indices],y.iloc[val\_indices]
>
>
>
> model.fit(X=x\_train,y=y\_train)
>
> train\_pred=np.append(train\_pred,model.predict(x\_val))
>
> test\_pred=np.append(test\_pred,model.predict(test))
>
> return test\_pred.reshape(-1,1),train\_pred
>
现在我们将创建两个基本模型:决策树和knn。
>
> model1 = tree.DecisionTreeClassifier(random\_state=1)
>
>
>
> test\_pred1 ,train\_pred1=Stacking(model=model1,n\_fold=10, train=x\_train,test=x\_test,y=y\_train)
>
>
>
> train\_pred1=pd.DataFrame(train\_pred1)
>
> test\_pred1=pd.DataFrame(test\_pred1)
>
>
>
> model2 = KNeighborsClassifier()
>
>
>
> test\_pred2 ,train\_pred2=Stacking(model=model2,n\_fold=10,train=x\_train,test=x\_test,y=y\_train)
>
>
>
> train\_pred2=pd.DataFrame(train\_pred2)
>
> test\_pred2=pd.DataFrame(test\_pred2)
>
创建第三个模型,逻辑回归,在决策树和knn模型的预测之上。
>
> df = pd.concat([train\_pred1, train\_pred2], axis=1)
>
> df\_test = pd.concat([test\_pred1, test\_pred2], axis=1)
>
>
>
> model = LogisticRegression(random\_state=1)
>
> model.fit(df,y\_train)
>
> model.score(df\_test, y\_test)
>
为了简化上面的解释,我们创建的堆叠模型只有两层。决策树和knn模型建立在零级,而逻辑回归模型建立在第一级。其实可以随意的在堆叠模型中创建多个层次。
###
#### 6.3.2 混合(Stacking)
混合遵循与堆叠相同的方法,但仅使用来自训练集的一个留出(holdout)/验证集来进行预测。换句话说,与堆叠不同,预测仅在留出集上进行。留出集和预测用于构建在测试集上运行的模型。以下是混合过程的详细说明:
**第一步:**原始训练数据被分为训练集合验证集。


**第二步:**在训练集上拟合模型。
**第三步:**在验证集和测试集上进行预测。


**第四步:**验证集及其预测用作构建新模型的特征。
**第五步:**该新模型用于对测试集和元特征(meta-features)进行最终预测。
**示例代码:**
我们将在训练集上建立两个模型,决策树和knn,以便对验证集进行预测。
>
> model1 = tree.DecisionTreeClassifier()
>
> model1.fit(x\_train, y\_train)
>
> val\_pred1=model1.predict(x\_val)
>
> test\_pred1=model1.predict(x\_test)
>
> val\_pred1=pd.DataFrame(val\_pred1)
>
> test\_pred1=pd.DataFrame(test\_pred1)
>
>
>
> model2 = KNeighborsClassifier()
>
> model2.fit(x\_train,y\_train)
>
> val\_pred2=model2.predict(x\_val)
>
> test\_pred2=model2.predict(x\_test)
>
> val\_pred2=pd.DataFrame(val\_pred2)
>
> test\_pred2=pd.DataFrame(test\_pred2)
>
结合元特征和验证集,构建逻辑回归模型以对测试集进行预测。
>
> df\_val=pd.concat([x\_val, val\_pred1,val\_pred2],axis=1)
>
> df\_test=pd.concat([x\_test, test\_pred1,test\_pred2],axis=1)
>
>
>
> model = LogisticRegression()
>
> model.fit(df\_val,y\_val)
>
> model.score(df\_test,y\_test)
>
###
#### 6.3.3 Bagging
Bagging背后的想法是结合多个模型的结果(例如,所有决策树)来获得泛化的结果。这有一个问题:如果在同样一组数据上创建所有模型并将其组合起来,它会有用吗?这些模型极大可能会得到相同的结果,因为它们获得的输入相同。那我们该如何解决这个问题呢?其中一种技术是自举(bootstrapping)。
Bootstrapping是一种采样技术,我们有放回的从原始数据集上创建观察子集,子集的大小与原始集的大小相同。
Bagging(或Bootstrap Aggregating)技术使用这些子集(包)来获得分布的完整概念(完备集)。为bagging创建的子集的大小也可能小于原始集。


**第一步:**从原始数据集有放回的选择观测值来创建多个子集。
**第二步:**在每一个子集上创建一个基础模型(弱模型)。
**第三步:**这些模型同时运行,彼此独立。
**第四步:**通过组合所有模型的预测来确定最终预测。


###
#### 6.3.4 Boosting
在我们进一步讨论之前,这里有另一个问题:如果第一个模型错误地预测了某一个数据点,然后接下来的模型(可能是所有模型),将预测组合起来会提供更好的结果吗?Boosting就是来处理这种情况的。
Boosting是一个顺序过程,每个后续模型都会尝试纠正先前模型的错误。后续的模型依赖于之前的模型。接下来一起看看boosting的工作方式:
**第一步:**从原始数据集创建一个子集。
**第二步:**最初,所有数据点都具有相同的权重。
**第三步:**在此子集上创建基础模型。
**第四步:**该模型用于对整个数据集进行预测。
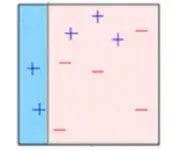
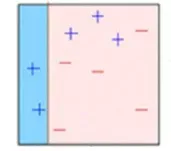
**第五步:**使用实际值和预测值计算误差。
**第六步:**预测错误的点获得更高的权重。(这里,三个错误分类的蓝色加号点将被赋予更高的权重)
**第七步:**创建另一个模型并对数据集进行预测(此模型尝试更正先前模型中的错误)。
### 最后的话
最近很多小伙伴找我要Linux学习资料,于是我翻箱倒柜,整理了一些优质资源,涵盖视频、电子书、PPT等共享给大家!
### 资料预览
给大家整理的视频资料:

给大家整理的电子书资料:

**如果本文对你有帮助,欢迎点赞、收藏、转发给朋友,让我有持续创作的动力!**
**网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。**
**[需要这份系统化的资料的朋友,可以点击这里获取!](https://bbs.csdn.net/topics/618542503)**
**一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!**
pred1)
>
> test\_pred1=pd.DataFrame(test\_pred1)
>
>
>
> model2 = KNeighborsClassifier()
>
> model2.fit(x\_train,y\_train)
>
> val\_pred2=model2.predict(x\_val)
>
> test\_pred2=model2.predict(x\_test)
>
> val\_pred2=pd.DataFrame(val\_pred2)
>
> test\_pred2=pd.DataFrame(test\_pred2)
>
结合元特征和验证集,构建逻辑回归模型以对测试集进行预测。
>
> df\_val=pd.concat([x\_val, val\_pred1,val\_pred2],axis=1)
>
> df\_test=pd.concat([x\_test, test\_pred1,test\_pred2],axis=1)
>
>
>
> model = LogisticRegression()
>
> model.fit(df\_val,y\_val)
>
> model.score(df\_test,y\_test)
>
###
#### 6.3.3 Bagging
Bagging背后的想法是结合多个模型的结果(例如,所有决策树)来获得泛化的结果。这有一个问题:如果在同样一组数据上创建所有模型并将其组合起来,它会有用吗?这些模型极大可能会得到相同的结果,因为它们获得的输入相同。那我们该如何解决这个问题呢?其中一种技术是自举(bootstrapping)。
Bootstrapping是一种采样技术,我们有放回的从原始数据集上创建观察子集,子集的大小与原始集的大小相同。
Bagging(或Bootstrap Aggregating)技术使用这些子集(包)来获得分布的完整概念(完备集)。为bagging创建的子集的大小也可能小于原始集。


**第一步:**从原始数据集有放回的选择观测值来创建多个子集。
**第二步:**在每一个子集上创建一个基础模型(弱模型)。
**第三步:**这些模型同时运行,彼此独立。
**第四步:**通过组合所有模型的预测来确定最终预测。


###
#### 6.3.4 Boosting
在我们进一步讨论之前,这里有另一个问题:如果第一个模型错误地预测了某一个数据点,然后接下来的模型(可能是所有模型),将预测组合起来会提供更好的结果吗?Boosting就是来处理这种情况的。
Boosting是一个顺序过程,每个后续模型都会尝试纠正先前模型的错误。后续的模型依赖于之前的模型。接下来一起看看boosting的工作方式:
**第一步:**从原始数据集创建一个子集。
**第二步:**最初,所有数据点都具有相同的权重。
**第三步:**在此子集上创建基础模型。
**第四步:**该模型用于对整个数据集进行预测。


**第五步:**使用实际值和预测值计算误差。
**第六步:**预测错误的点获得更高的权重。(这里,三个错误分类的蓝色加号点将被赋予更高的权重)
**第七步:**创建另一个模型并对数据集进行预测(此模型尝试更正先前模型中的错误)。
### 最后的话
最近很多小伙伴找我要Linux学习资料,于是我翻箱倒柜,整理了一些优质资源,涵盖视频、电子书、PPT等共享给大家!
### 资料预览
给大家整理的视频资料:
[外链图片转存中...(img-t2eGoFSJ-1715007470389)]
给大家整理的电子书资料:
[外链图片转存中...(img-JHctoAHe-1715007470389)]
**如果本文对你有帮助,欢迎点赞、收藏、转发给朋友,让我有持续创作的动力!**
**网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。**
**[需要这份系统化的资料的朋友,可以点击这里获取!](https://bbs.csdn.net/topics/618542503)**
**一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!**






















 6972
6972

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








