最新算法-效率的度量和函数的渐进增长_算法分析,等效率函数，2024年最新面试大厂应该注意哪些问题

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化的资料的朋友，可以点击这里获取！

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

显然，第一种算法，执行了 1+ ( n+1 ) +n+1 次 =2n+3次; 而第二种算法，是1+1+1=3 次。事实上两个算法的第一条和最后一条语句是一样的，所以我们关注的代码其实是中间的那部分，我们把循环看作一个整体，忽略头尾循环判断的开销， 那么这两个算法其实就是 n 次与 1 次的差距。算法好坏显而易见。

我们再来延伸一下上面这个例子:

int i,j,x=0,sum=0, n = 100;		/* 执行1次 */
   for(i = 1; i <= n; i++){
       for(j = 1; j <= n; j++){
 	   x++;					/* 执行n×n次 */
	   sum+=x;
       }
    }
System.out.println(sum);		/* 执行1次 */

这个例子中， i 从 1 到 100 ，每次都要让 j 循环 100 次，而当中的 x++和 sum+=x ; 其实就1+2+3+…+10000 ，也就是 100^2 (100的2次方)次，所以这个算法当中，循环部分的代码整体需要执行 n^2 (忽略循环体头尾的开销)次。显然这个算法的执行次数对于同样的输入规模 n =100 ， 要多于前面两种算法，这个算法的执行时间随着 n 的增加也将远远多于前面两个。

此时你会看到，测定运行时间最可靠的方法就是计算对运行时间有消耗的基本操作的执行次数， 运行时间与这个计数成正比。

我们不关心编写程序所用的程序设计语言是什么，也不关心这些程序将跑在什么样的计算机中，我们只关心它所实现的算法。这样，不计那些循环索引的递增和循环终止条件、 变量声明、打印结果等操作， 最终，在分析程序的运行时间时，最重要的是把程序看成是独立于程序设计语言的算法或一系列步骤。

可以从问题描述中得到启示，同样问题的输入规模是 n ，求和算法的第一种，求1+2+… +n 需要一段代码运行 n 次 。那么这个问题的输入规模使得操作数量是 f ( n)= n ，显然运行 100 次的同一段代码规模是运算 10 次的 10 倍。而第二种，无论 n 为多少，运行次数都为 1 ，即 f (n) =1 ; 第三种，运算 100 次是运算 10 次的 100倍。因为它是 f (n) =n^2 。

我们在分析一个算法的运行时间时，重要的是把基本操作的数量与输入规模关联起来，即基本操作的数量必须表示成输入规模的函数(如图 2-7-1 所示) 。

我们可以这样认为，随着 n 值的越来越大，它们在时间效率上的差异也就越来越大 。好比你们当中有些人每天都在学习，我指有用的学习，而不是只为考试的死读书 ， 每天都在进步，而另一些人，打打游戏，睡睡大觉。 入校时大家都一样 ， 但毕业时结果可能就大不一样，前者名企争抢着要，后者求职无门 。

2.8 函数的渐近增长

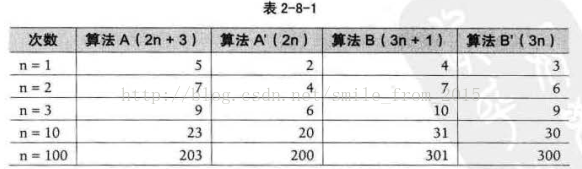
我们现在来判断一下，两个算法 A 和 B 哪个更好。 假设两个算法的输入规模都是n ，算法 A 要做 2n + 3 次操作，你可以理解为先有一个 n 次的循环 ，执行完成后，再有一于 n 次循环，最后有三次赋值或运算，共 2n + 3 次操作。 算法 B 要做 3n + 1 次操作。 你觉得它们谁更快呢?

准确说来，答案是不一定的(如表 2-8-1 所示)。

当 n = 1 时，算法 A 效率不如算法 B (次数比算法 B 要多一次)。 而当 n = 2时，两者效率相同 ; 当 n>2 时，算法 A 就开始优于算法 B 了，随着 n 的增加，算法 A 比算法 B 越来越好了: (执行的次数比 B 要少)。于是我们可以得出结论，算法 A 总体上要好过算法 B 。

此时我们给出这样的定义，输入规模 n 在没有限制的情况下，只要超过一个数值N ，这个函数就总是大于另一个函数，我的称函数是渐近增长的。

函数的渐近增长:给定两个函数 f(n)和g(n)， 如果存在-个整数 N ，使得对于所有的 n>N, f(n)总是比g(n)大，那么 ， 我们说f(n)的增长渐近快于 g(n)。

从中我们发现，随着 n 的增大，后面的 +3 还是 +1 其实是不影响最终的算法变化的，例如算法 A’ 与算法 B ’ ，所以， 我们可以忽略这些加法常数。 后面的例子，这样的常数被忽略的意义可能会更加明显 。

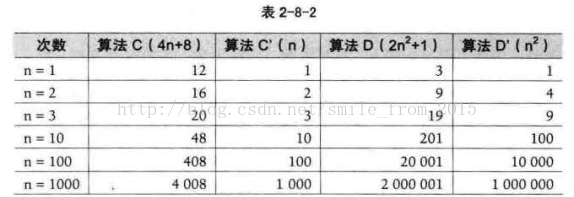
我们来看第二个例子，算法 C 是 4n+8 ，算法 D 是 2n^2 + 1 (如表 2-8-2 所示) 。

当 n <= 3 的时候，算法 C 要差于算法 D (因为算法 C 次数 比较多) ，但当 n > 3后，算法 C 的优势就越来越优于算法D了，到后来更是远远胜过。而当后面的常数去掉后，我们发现其实结果没有发生改变。 甚至我们再观察发现， 哪怕去掉与 n 相乘的常数，这样的结果也没发生改变，算法 C 的次数随着 n 的增长，还是远小于算法D 。 也就是说， 与最高次项相乘的常数并不重要。

我们再来看第三个例子。算法 E 是 2n^2(n的2次方) + 3n + 1 ，算法 F 是 2n^3 + 3n + 1 (如表2-8-3 所示)。

当 n=l 的时候 ，算法E与算法 F 结果相同，但当 n>l 后 ， 算法E的优势就要开始优于算法F，随着 n 的增大，差异非常明显。通过观察发现，最高次项的指数大的，函数随着 n 的增长，结果也会变得增长特别快。

我们来看最后一个例子。算法G是 2n^2，算法 H 是 3n + 1 ， 算法 I 是 2n^2 + 3n + 1(如表 2-8-4 所示) 。

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化的资料的朋友，可以点击这里获取！

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！