P1004 [NOIP 2000 提高组] 方格取数

_码力全开_

于 2025-10-12 20:27:42 发布

阅读量259

点赞数 9

CC 4.0 BY-SA版权

分类专栏：洛谷答案文章标签：算法动态规划 python c++ c语言 java go

本文链接：https://blog.csdn.net/2401_84134448/article/details/153136026

洛谷答案专栏收录该内容

3 篇文章

订阅专栏

题目背景

NOIP 2000 提高组 T4

题目描述

设有 $\times N$ 的方格图 $\le 9)$ ，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字 $0$ 。如下图所示（见样例）:

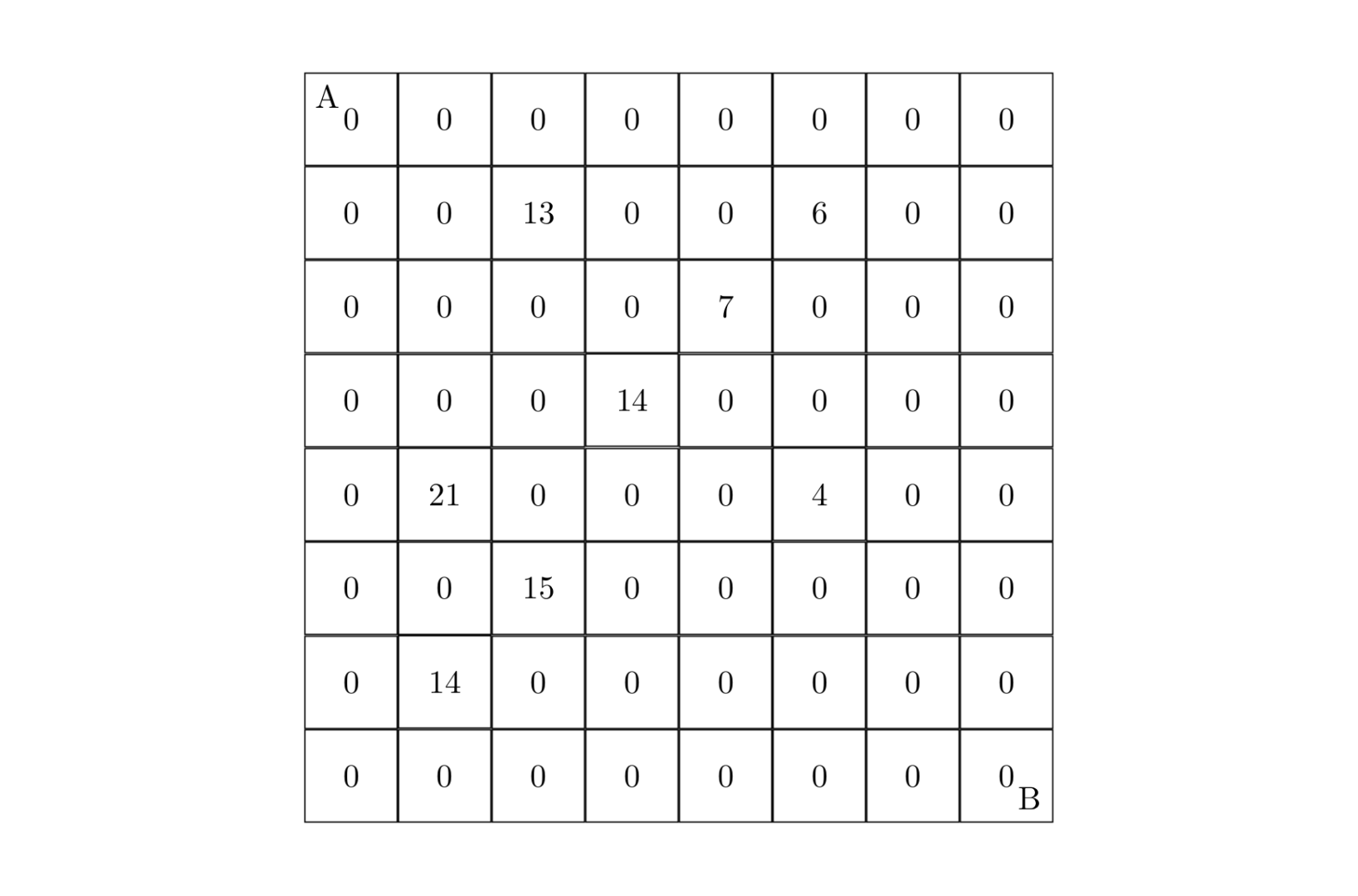
某人从图的左上角的 $A$ 点出发，可以向下行走，也可以向右走，直到到达右下角的 $B$ 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 $0$ ）。
此人从 $A$ 点到 $B$ 点共走两次，试找出 $2$ 条这样的路径，使得取得的数之和为最大。

输入格式

输入的第一行为一个整数 $N$ （表示 $\times N$ 的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的 $0$ 表示输入结束。

输出格式

只需输出一个整数，表示 $2$ 条路径上取得的最大的和。

输入输出样例 #1

输入 #1

输出 #1

说明/提示

数据范围： $1≤N≤91\le N\le 9$ 。

答案

C++

#include <iostream>
#include <algorithm>
using namespace std;

int n;
int map_[10][10];
int dp[10][10][10][10];

int main()
{
    cin >> n;
    int x, y, val;
    while (cin >> x >> y >> val && (x || y || val))
    {
        map_[x][y] = val;
    }

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            for (int k = 1; k <= n; k++)
            {
                for (int l = 1; l <= n; l++)
                {
                    dp[i][j][k][l] = max(
                        max(dp[i-1][j][k-1][l], dp[i-1][j][k][l-1]),
                        max(dp[i][j-1][k-1][l], dp[i][j-1][k][l-1])
                    ) + map_[i][j];
                    
                    if (i != k || j != l)
                    {
                        dp[i][j][k][l] += map_[k][l];
                    }
                }
            }
        }
    }

    cout << dp[n][n][n][n] << endl;
    return 0;
}

C

#include <stdio.h>
#include <stdlib.h>

int max4(int a, int b, int c, int d)
{
    int max = a;
    if (b > max) max = b;
    if (c > max) max = c;
    if (d > max) max = d;
    return max;
}

int main()
{
    int n;
    scanf("%d", &n);
    int map[10][10] = {0};
    int x, y, val;
    
    while (1)
    {
        scanf("%d %d %d", &x, &y, &val);
        if (x == 0 && y == 0 && val == 0)
            break;
        map[x][y] = val;
    }
    
    int dp[10][10][10][10] = {0};
    
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            for (int k = 1; k <= n; k++)
            {
                for (int l = 1; l <= n; l++)
                {
                    dp[i][j][k][l] = max4(
                        dp[i-1][j][k-1][l],
                        dp[i-1][j][k][l-1],
                        dp[i][j-1][k-1][l],
                        dp[i][j-1][k][l-1]
                    ) + map[i][j];
                    
                    if (i != k || j != l)
                    {
                        dp[i][j][k][l] += map[k][l];
                    }
                }
            }
        }
    }
    
    printf("%d\n", dp[n][n][n][n]);
    return 0;
}

Python

n = int(input())
grid = [[0] * (n + 1) for _ in range(n + 1)]

while True:
    line = list(map(int, input().split()))
    x, y, val = line[0], line[1], line[2]
    if x == 0 and y == 0 and val == 0:
        break
    grid[x][y] = val

dp = [[[[0] * (n + 1) for _ in range(n + 1)] 
       for __ in range(n + 1)] for ___ in range(n + 1)]

for i in range(1, n + 1):
    for j in range(1, n + 1):
        for k in range(1, n + 1):
            for l in range(1, n + 1):
                max_val = max(
                    dp[i-1][j][k-1][l],
                    dp[i-1][j][k][l-1],
                    dp[i][j-1][k-1][l],
                    dp[i][j-1][k][l-1]
                )
                dp[i][j][k][l] = max_val + grid[i][j]
                
                if i != k or j != l:
                    dp[i][j][k][l] += grid[k][l]

print(dp[n][n][n][n])

Java

import java.util.Scanner;

public class GridNumber {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int[][] grid = new int[n + 1][n + 1];
        
        while (true) {
            int x = scanner.nextInt();
            int y = scanner.nextInt();
            int val = scanner.nextInt();
            if (x == 0 && y == 0 && val == 0) {
                break;
            }
            grid[x][y] = val;
        }
        
        int[][][][] dp = new int[n + 1][n + 1][n + 1][n + 1];
        
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                for (int k = 1; k <= n; k++) {
                    for (int l = 1; l <= n; l++) {
                        int maxVal = Math.max(
                            Math.max(dp[i-1][j][k-1][l], dp[i-1][j][k][l-1]),
                            Math.max(dp[i][j-1][k-1][l], dp[i][j-1][k][l-1])
                        );
                        dp[i][j][k][l] = maxVal + grid[i][j];
                        
                        if (i != k || j != l) {
                            dp[i][j][k][l] += grid[k][l];
                        }
                    }
                }
            }
        }
        
        System.out.println(dp[n][n][n][n]);
        scanner.close();
    }
}

Go

package main

import (
	"fmt"
)

func max4(a, b, c, d int) int {
	maxVal := a
	if b > maxVal {
		maxVal = b
	}
	if c > maxVal {
		maxVal = c
	}
	if d > maxVal {
		maxVal = d
	}
	return maxVal
}

func main() {
	var n int
	fmt.Scan(&n)
	grid := make([][]int, n+1)
	for i := range grid {
		grid[i] = make([]int, n+1)
	}

	var x, y, val int
	for {
		fmt.Scan(&x, &y, &val)
		if x == 0 && y == 0 && val == 0 {
			break
		}
		grid[x][y] = val
	}

	dp := make([][][][]int, n+1)
	for i := range dp {
		dp[i] = make([][][]int, n+1)
		for j := range dp[i] {
			dp[i][j] = make([][]int, n+1)
			for k := range dp[i][j] {
				dp[i][j][k] = make([]int, n+1)
			}
		}
	}

	for i := 1; i <= n; i++ {
		for j := 1; j <= n; j++ {
			for k := 1; k <= n; k++ {
				for l := 1; l <= n; l++ {
					dp[i][j][k][l] = max4(
						dp[i-1][j][k-1][l],
						dp[i-1][j][k][l-1],
						dp[i][j-1][k-1][l],
						dp[i][j-1][k][l-1],
					) + grid[i][j]

					if i != k || j != l {
						dp[i][j][k][l] += grid[k][l]
					}
				}
			}
		}
	}

	fmt.Println(dp[n][n][n][n])
}