最后
不知道你们用的什么环境,我一般都是用的Python3.6环境和pycharm解释器,没有软件,或者没有资料,没人解答问题,都可以免费领取(包括今天的代码),过几天我还会做个视频教程出来,有需要也可以领取~
给大家准备的学习资料包括但不限于:
Python 环境、pycharm编辑器/永久激活/翻译插件
python 零基础视频教程
Python 界面开发实战教程
Python 爬虫实战教程
Python 数据分析实战教程
python 游戏开发实战教程
Python 电子书100本
Python 学习路线规划

网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!
=
f
[
i
−
1
]
f
[
i
−
2
]
f[i] = f[i-1] + f[i-2]
f[i]=f[i−1]+f[i−2] 就是一个简单的状态转移方程)。
- 下文第四节会图解常用的状态转移方程。
3、最优化原理和最优子结构
- 如果问题的最优解包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优化原理。这里我尽力减少理论化的概念,而改用一个简单的例题来加深对这句话的理解。
【例题3】给定一个长度为
n
(
1
<
=
n
<
=
1000
)
n(1 <= n <= 1000)
n(1<=n<=1000) 的整数序列
a
[
i
]
a[i]
a[i],求它的一个子序列 (子序列即在原序列任意位置删除0或多个元素后的序列),满足如下条件:
1、该序列单调递增;
2、在所有满足条件 1 的序列中长度是最长的;
- 这个问题是经典的动态规划问题,被称为最长单调子序列。
- 我们假设现在没有任何动态规划的基础,那么看到这个问题首先想到的是什么?
- 我想到的是万金油算法—深度优先搜索(
D
F
S
DFS
DFS ),即枚举
a
[
i
]
a[i]
a[i] 这个元素取或不取,所有取的元素组成一个合法的子序列,枚举的时候需要满足单调递增这个限制,那么对于一个
n
n
n 个元素的序列,最坏时间复杂度自然就是
O
(
2
n
)
O(2^n)
O(2n) ,
n
=
30
n = 30
n=30 就已经很变态了更别说是
1000
1000
1000。
- 然而,方向是对的,动态规划求解之前先试想一下搜索的正确性,这里搜索的正确性是很显然的,因为已经枚举了所有情况,总有一种情况是我们要求的解。我们尝试将搜索的算法进行一些改进,假设第
i
i
i 个数取的情况下已经搜索出的最大长度记录在数组中,即用
d
[
i
]
d[i]
d[i] 表示当前搜索到的以
a
[
i
]
a[i]
a[i] 结尾的最长单调子序列的长度,那么如果下次搜索得到的序列长度小于等于
d
[
i
]
d[i]
d[i],就不必往下搜索了(因为即便继续往后枚举,能够得到的解必定不会比之前更长);反之,则需要更新
d
[
i
]
d[i]
d[i] 的值。
- 如图二-3-1,红色路径表示第一次搜索得到的一个最长子序列1、2、3、5,蓝色路径表示第二次搜索,当枚举第3个元素取的情况时,发现以第3个数结尾的最长长度
d
[
3
]
=
3
d[3] = 3
d[3]=3,比本次枚举的长度要大(本次枚举的长度为2),所以放弃往下枚举,大大减少了搜索的状态空间。

图二-3-1
- 这时候,我们其实已经不经意间设计好了状态,就是上文中提到的那个
d
[
i
]
d[i]
d[i] 数组,它表示的是以
a
[
i
]
a[i]
a[i] 结尾的最长单调子序列的长度,那么对于任意的
i
i
i,
d
[
i
]
d[i]
d[i] 一定等于
d
[
j
]
1
(
j
<
i
)
d[j] + 1 \ ( j < i )
d[j]+1 (j<i),而且还得满足
a
[
j
]
<
a
[
i
]
a[j] < a[i]
a[j]<a[i]。因为这里的
d
[
i
]
d[i]
d[i] 表示的是最长长度,所以
d
[
i
]
d[i]
d[i] 的表达式可以更加明确,即:
d
[
i
]
=
m
a
x
(
d
[
j
]
∣
j
<
i
,
a
[
j
]
<
a
[
i
]
)
1
d[i] = max ( d[j] | j < i, a[j] < a[i] ) + 1
d[i]=max(d[j]∣j<i,a[j]<a[i])+1
- 这个表达式很好的阐释了最优化原理,其中
d
[
j
]
d[j]
d[j] 作为
d
[
i
]
d[i]
d[i] 的子问题,
d
[
i
]
d[i]
d[i] 最长(优)当且仅当
d
[
j
]
d[j]
d[j] 最长(优)。当然,这个方程就是这个问题的状态转移方程。状态总数量
O
(
n
)
O(n)
O(n), 每次转移需要用到前
i
i
i 项的结果,平摊下来也是
O
(
n
)
O(n)
O(n) 的, 所以该问题的时间复杂度是
O
(
n
2
)
O(n^2)
O(n2)。
4、决策和无后效性
- 一个状态演变到另一个状态,往往是通过“决策”来进行的。有了“决策”,就会有状态转移。而无后效性,就是一旦某个状态确定后,它之前的状态无法对它之后的状态产生“效应”(影响)。
【例题4】老王想在未来的
n
n
n 年内每年都持有电脑,
m
(
y
,
z
)
m(y, z)
m(y,z) 表示第
y
y
y 年到第
z
z
z 年的电脑维护费用,其中
y
y
y 的范围为
[
1
,
n
]
[1, n]
[1,n],
z
z
z 的范围为
[
y
,
n
]
[y, n]
[y,n],
c
c
c 表示买一台新的电脑的固定费用。 给定矩阵
m
m
m,固定费用
c
c
c,求在未来
n
n
n 年都有电脑的最少花费。
- 考虑第
i
i
i 年是否要换电脑,换和不换是不一样的决策,那么我们定义一个二元组
(
a
,
b
)
(a, b)
(a,b),其中
a
<
b
a < b
a<b,它表示了第 a 年和第 b 年都要换电脑(第 a 年和第 b 年之间不再换电脑),如果假设我们到第 a 年为止换电脑的最优方案已经确定,那么第 a 年以前如何换电脑的一些列步骤变得不再重要,因为它并不会影响第 b 年的情况,这就是无后效性。
- 接下来,会对这题进行一个详细的解释,当然看不懂没关系,可以跳过这个步骤,直接去看 第三章 - 动态规划的经典模型。毕竟,本文是入门级别的,后面还会花更多的时间来讲解动态规划的内容,可以和搜索一起逐步理解状态的概念。
- 更加具体得,令
d
[
i
]
d[i]
d[i] 表示在第 i 年买了一台电脑的最小花费(由于这台电脑能用多久不确定,所以第 i 年的维护费用暂时不计在这里面),如果上一次更换电脑的时间在第 j 年,那么第 j 年更换电脑到第 i 年之前的总开销就是
c
m
(
j
,
i
−
1
)
c + m(j, i-1)
c+m(j,i−1)
- 于是有状态转移方程:
d
[
i
]
=
m
i
n
(
d
[
j
]
m
(
j
,
i
−
1
)
∣
1
<
=
j
<
i
)
c
d[i] = min( d[j] + m(j, i-1) | 1 <= j < i ) + c
d[i]=min(d[j]+m(j,i−1)∣1<=j<i)+c
- 这里的
d
[
i
]
d[i]
d[i] 并不是最后问题的解,因为它漏算了第 i 年到第 n 年的维护费用,所以最后问题的答案:
a
n
s
=
m
i
n
(
d
[
i
]
m
(
i
,
n
)
∣
1
<
=
i
<
n
)
ans = min( d[i] + m(i, n) | 1 <= i < n )
ans=min(d[i]+m(i,n)∣1<=i<n)
- 我们发现两个方程看起来很类似,其实是可以合并的,我们可以假设第 n+1 年必须换电脑,并且第 n+1 年换电脑的费用为 0,那么整个阶段的状态转移方程就是:
d
[
i
]
=
m
i
n
(
d
[
j
]
m
(
j
,
i
−
1
)
∣
1
<
=
j
<
i
)
w
(
i
)
d[i] = min( d[j] + m(j, i-1) | 1 <= j < i ) + w(i)
d[i]=min(d[j]+m(j,i−1)∣1<=j<i)+w(i)
w
(
i
)
=
{
c
i
<
n
1
0
i
=
n
1
w(i) = \begin{cases} c & i < n+1\ 0 & i=n+1 \end{cases}
w(i)={c0i<n+1i=n+1
- d
[
n
1
]
d[n+1]
d[n+1] 就是我们需要求的最小费用了。
三、动态规划的经典模型
- 本章节作者会通过图的方式,带读者了解一些基本模型,以加深对动态规划状态的理解;
- 黄色 ■ 代表当前状态;
- 绿色 ■ 代表子状态(已经求出的状态);
- 红色 ■ 代表尚未求出的状态;
- 灰色 ■ 代表永远不存在的状态;
1、线性模型
- 线性模型是动态规划中最常见的模型,上文讲到的最长单调子序列就是经典的线性模型。
- 线性模型的状态一般是通过 一维数组表示的,如图三-1-1所示,图中黄色块的状态为
d
[
i
]
d[i]
d[i],绿色块的状态为
d
[
j
]
d[j]
d[j],并且满足
(
j
<
i
)
(j < i)
(j<i),只有当
d
[
j
]
d[j]
d[j] 全部计算出来以后,
d
[
i
]
d[i]
d[i]的值才能够被确定。

图三-1-1
- 线性模型最经典的问题莫过于 背包问题 了,有关背包问题的内容,可以参考以下这篇文章:夜深人静写算法(十九)- 背包总览。
2、区间模型
- 对比线性模型,区间模型状态一般是通过:一个二维数组来表示的。
- 区间模型的状态表示一般为
d
[
i
]
[
j
]
d[i][j]
d[i][j],表示区间
[
i
,
j
]
[i, j]
[i,j] 上的最优解,最终要求的肯定是
[
1
,
n
]
[1, n]
[1,n] 的最优解。
- 如图三-2-1所示,既然是表示区间,所以对于状态
d
[
i
]
[
j
]
d[i][j]
d[i][j],当
i
j
i>j
i>j时,肯定是不合法的状态,所以标记为灰色;
d
[
i
]
[
j
]
d[i][j]
d[i][j] 表当前状态,标记为黄色;

图三-2-1
- 区间模型的详细内容可以参考以下这篇文章:夜深人静写算法(二十七)- 区间DP。
3、树状模型
- 树形动态规划(树形DP),是指状态图是一棵树,状态转移也发生在树上,父结点的状态值通过所有子结点状态值计算完毕后得出,后续会专门开辟一个章节来讲述树形动态规划。
- 状态表示如图三-3-1所示。

图三-3-1
4、状态压缩模型
- 状态压缩的含义其实是对状态进行重新编码,来看下面这个例子。
- 假设状态是一个五维的数组,并且每一维的取值为
[
0
,
3
]
[0,3]
[0,3],状态表示如下:
d
[
a
]
[
b
]
[
c
]
[
d
]
[
e
]
(
0
<
=
a
,
b
,
c
,
d
,
e
<
=
3
)
d[a][b][c][d][e] \ (0 <= a,b,c,d,e <= 3)
d[a][b][c][d]e
- 那么,写代码的过程中需要操作五维数组,十分繁琐,我们可以通过将状态压缩,将它重新编码到一个一维数组中。
- 其实只要能够找到一个映射函数,满足
x
x
x 和
(
a
,
b
,
c
,
d
,
e
)
(a,b,c,d,e)
(a,b,c,d,e) 一一映射,即:
f
(
x
)
=
(
a
,
b
,
c
,
d
,
e
)
f(x) = (a,b,c,d,e)
f(x)=(a,b,c,d,e)
- 因为每一维的取值为
[
0
,
3
]
[0,3]
[0,3],我们可以把每一维当成是 4进制数的每一位,于是有:
- x
=
a
×
4
4
b
×
4
3
c
×
4
2
d
×
4
1
e
×
4
0
x = a \times 4^4 + b \times 4^3 + c \times 4^2 + d \times 4^1 + e \times 4^0
x=a×44+b×43+c×42+d×41+e×40
- 那么,我们只需要用一个一维数组来表示状态即可:
d
[
x
]
d[x]
d[x]。
四、动态规划的常用状态转移方程
动态规划算法三要素(摘自黑书,总结的很好,很有概括性):
①所有不同的子问题组成的表
②解决问题的依赖关系可以看成是一个图
③填充子问题的顺序(即对②的图进行拓扑排序,填充的过程称为状态转移);
- 则如果子问题的数目为
O
(
n
t
)
O(n^t)
O(nt),每个子问题需要用到
O
(
n
e
)
O(n^e)
O(ne) 个子问题的结果,那么我们称它为 tD/eD 的问题,于是可以总结出四类常用的动态规划方程:(下面会把opt作为取最优值的函数(一般取
m
i
n
min
min 或
m
a
x
max
max ),
w
(
j
,
i
)
w(j, i)
w(j,i)为一个实函数,其它变量都可以在常数时间计算出来)。
1、1D/1D
- d
[
i
]
=
o
p
t
(
d
[
j
]
w
(
j
,
i
)
∣
0
<
=
i
<
j
)
d[i] = opt( d[j] + w(j, i) | 0 <= i < j )
d[i]=opt(d[j]+w(j,i)∣0<=i<j)
- 状态转移如图四-1-1所示(黄色块代表
d
[
i
]
d[i]
d[i],绿色块代表
d
[
j
]
d[j]
d[j]):

图四-1-1
- 这类状态转移方程一般出现在线性模型中。
2、2D/0D
- d
[
i
]
[
j
]
=
o
p
t
(
d
[
i
−
1
]
[
j
]
x
i
,
d
[
i
]
[
j
−
1
]
y
j
,
d
[
i
−
1
]
[
j
−
1
]
z
i
j
)
d[i][j] = opt( d[i-1][j] + x_i, d[i][j-1] + y_j, d[i-1][j-1] + z_{ij} )
d[i][j]=opt(d[i−1][j]+xi,d[i][j−1]+yj,d[i−1][j−1]+zij)
- 状态转移如图四-2-1所示:
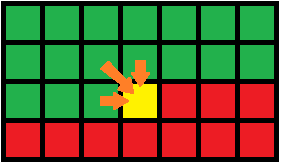
图四-2-1
- 比较经典的问题是最长公共子序列、最小编辑距离。
- 有关最长公共子序列的问题,可以参考以下文章:夜深人静写算法(二十一)- 最长公共子序列
- 有关最小编辑距离的问题,可以参考以下文章:夜深人静写算法(二十二)- 最小编辑距离
3、2D/1D
- d
[
i
]
[
j
]
=
w
(
i
,
j
)
o
p
t
(
d
[
i
]
[
k
−
1
]
d
[
k
]
[
j
]
)
d[i][j] = w(i, j) + opt( d[i][k-1] + d[k][j] )
d[i][j]=w(i,j)+opt(d[i][k−1]+d[k][j])
- 区间模型常用方程,如图四-3-1所示:
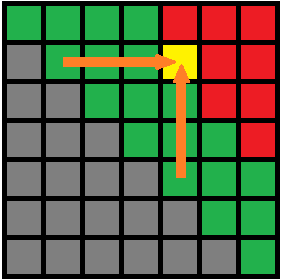
四-3-1
- 另外一种常用的 2D/1D 的方程为:
- d
[
i
]
[
j
]
=
o
p
t
(
d
[
i
−
1
]
[
k
]
w
(
i
,
j
,
k
)
∣
k
<
j
)
d[i][j] = opt( d[i-1][k] + w(i, j, k) | k < j )
d[i][j]=opt(d[i−1][k]+w(i,j,k)∣k<j)
-
- 区间模型的详细内容可以参考以下这篇文章:夜深人静写算法(二十七)- 区间DP
4、2D/2D
- d
[
i
]
[
j
]
=
o
p
t
(
d
[
i
′
]
[
j
′
]
w

感谢每一个认真阅读我文章的人,看着粉丝一路的上涨和关注,礼尚往来总是要有的:
① 2000多本Python电子书(主流和经典的书籍应该都有了)
② Python标准库资料(最全中文版)
③ 项目源码(四五十个有趣且经典的练手项目及源码)
④ Python基础入门、爬虫、web开发、大数据分析方面的视频(适合小白学习)
⑤ Python学习路线图(告别不入流的学习)
网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








